- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
FDTD与DFT在分析开口微波加热器中的应用
录入:edatop.com 点击:
FDTD与DFT在分析开口微波加热器中的应用
陈绍乎
(安徽大学电子工程系,合肥 230039)
摘 要:本文应用时域有限差分法(FDTD)和高散傅立叶变换(DFT)分析和计算了一种开口式同轴加热装置内部谐振场和外部辐射场,给出了使用两种不同激励源以及是否使用扼流槽后的场的结果。测量结果显示了这种方法的准确性。这种可移动的开口式加热器可以方便地提升对材料进行热处理的温度。
关键词:微波加热,时域有限差分,离散傅立叶变换
1 引言
随着微波技术日益渗入生产和日常生活领域,微波加热技术正在得到越来越广泛的应用,因而设计各种不同用途的微波加热器非常有意义。由于结构的复杂性,理论计算已无法进行,只能使用数值计算方法。本文应用时域有限差分(FDTD)法,并结合Mur的第一类边界条件,分析和计算了一种开口式的微波加热装置。通过对腔体输入功率大小的控制,该装置可以在开口的中心导体顶端产生700℃以上的高温,以达到处理不同非金属材料的要求和对材料进行焊接。本文准确地计算出了腔内和腔外的场强分布,以便了解腔内变换(DFT)技术,分别给出了在脉冲源激励和正弦稳态激励时,腔内外电场分布的计算结果,以了解用二种不同方法在计算时的差异性。针对腔体四周为仿止微波泄漏而设计的扼流槽,计算结果也说明了扼流槽的有效性,最后对腔内外电场的Ez分量进行了测量,并与计算结果进行了对比。
2 FDTD法的腔体分析
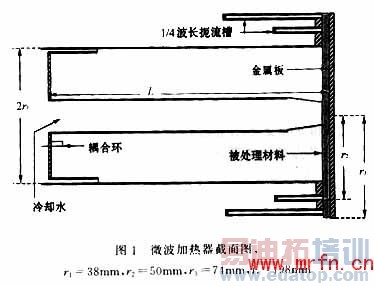
图1为开口式微波加热器的二维平面图。腔体前端放置一金属铜板,图中有斜线的阻影部分由金属良导体构成,颜色较浅的阻影部分是被处理的非金属材料,被处理材料可在腔体前端的金属铜板上平滑移动。
由理论分析可知,在腔体内产生电磁振荡时,由于在高温处理材料时,腔内能量较大,为了防止微波从开口处泄漏,在腔体四周设置了1/4波长的扼流槽,而两种不同长度的扼流槽分别工作于2.45Hz和915MHz,可通过调节腔体的长度来决定。
分析腔体的结构可以看出,因为腔体是放置对称且有一中心导体柱的开口式,类似同轴型结构,计算时主要考虑TM模式,计算的场量为Ez,Er分量[1]。这样,由麦克斯韦方程的相关形式可以得出:
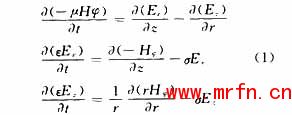
由于腔体的轴对称,只需要计算二维空间,并且从节省计算时间和机器内存考虑,只要计算轴对称的一半空间即可。采用精度较高的正方形网络划分以及中心差分的形式,可以将电场和磁场的相关分量表示成[2]:
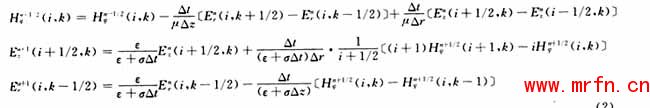
这里i,k分别表示r和z方向的网格标号或空间步长序号,△t是时间步长的个数,σ是非曲直电导率。由于腔体非封闭,腔体外有电磁能量分布,计算时使用了Mur的第一类边界条件加以处理[3],边界选在r=182mm,z=282mm处。
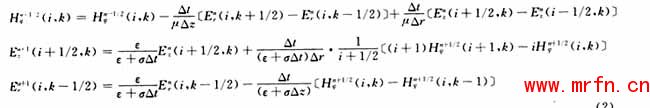
这里i,k分别表示r和z方向的网格标号或空间步长序号,△t是时间步长的个数,σ是非曲直电导率。由于腔体非封闭,腔体外有电磁能量分布,计算时使用了Mur的第一类边界条件加以处理[3],边界选在r=182mm,z=282mm处。
在本文的计算中,使用了两种激励源以便于比较。一种是谐振频率下的连续正弦激励,激励位置在腔体底端以模拟耦合环。这样,当腔内的场达到稳定状态后,取时域解的计算时间平均值,每个节点处场振幅的时间平均值由下式得出[4]:

这里N是总的时间步长次数。
这里N是总的时间步长次数。
另一方法是使用脉冲激励源而产生大量模式。通过对被计算时域响应的离散傅立叶变换,不仅可以在谐振频率处产生场强振幅的峰值,相应的谐振频率可以得出,而且由时域解的离散傅立叶变换,在相应频率下每个网格节点处的场强分布就可由下式得出[5]:
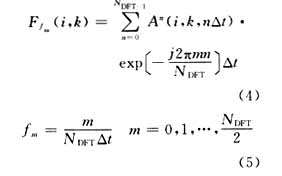
这里An是时域解,m是频率指数,NDFT是总的计算次数。
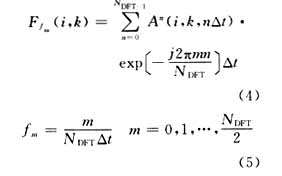
这里An是时域解,m是频率指数,NDFT是总的计算次数。
3 计算和实验结果
将图1的二维腔体(包括腔体外的一定区域)分成91△r×114△z的网格。考虑到空间和时间上的数值计算稳定性,采用的稳定条件为:△r=△z=2mm,
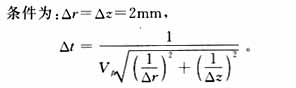
在计算过程中,将导体表面的切向电场分量设为零值,在空气和介质表面上的电场则使用(εr)/2的平均值来进行计算。在本文的实例中,介质区域的材料参数分别为εr μr=1.0。=2.0, σ=0.02,+ε0
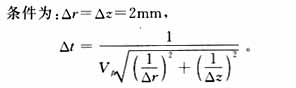
在计算过程中,将导体表面的切向电场分量设为零值,在空气和介质表面上的电场则使用(εr)/2的平均值来进行计算。在本文的实例中,介质区域的材料参数分别为εr μr=1.0。=2.0, σ=0.02,+ε0
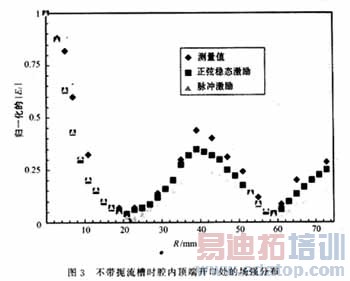
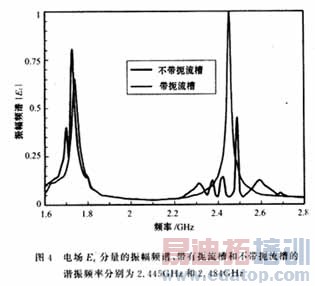
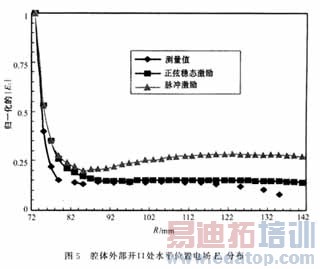
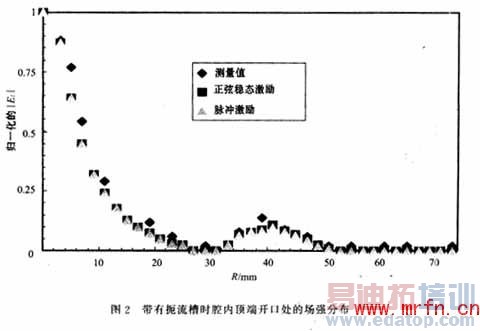
图2和图3分别给出了带有扼流槽和不带扼流槽的腔体在开口区域离开金属铜板为2mm处的电场z分量的分布。相应计算得出的谐振频率分别为2.445GHz和2.484GHz,如图4所示。测量频率的结果则分别为2.451GHz和2.50GHz。为防止大功率应用时,中心导体顶端打火,中心导体靠近处理材料的前5cm一段长度做成直径为20mm到8mm的圆弧状,测量则通过在被处理材料上的钨板上钻出一系列直径为1mm,并且长度一直深入材料达1mm的小孔来进行,而且涂有绝缘薄层材料的直径为0.8mm的同轴探头可以灵敏于从小孔中检测到被处理材料区域的电场z分量。图2中可以看出两种激励源的计算结果十分一对敌,而且与测量值十分接近。图3中靠近中心导体2cm以内处,两种结果仍然一致,在离中心2cm以外有一定的偏差。使用正弦稳定源的计算结果要更接近测量值,原因在于DFT是在FDTD的计算结果上进行的,这样增大了计算误差。从图2和图3可以看出,带有扼流槽的腔体在腔口边缘处的场强降到很低的程度,而不使用扼流槽则会有很强的微波辐射,因此FDTD计算结果显示出扼流槽在防止微波漏方面所起的重要作用,同时也提升了腔内中心处的场强。图5给出了不带扼流槽时腔体外部区域(75mm
4 结论
FDTD法除了用于计算天线幅射等一类问题以外,在计算带有开口区域的复杂微波腔体上也十分有效[1,6]。结合使用DFT则不仅可以计算出场强的分布,而且可以方便地计算出谐振频率,因此在设计微波装置时,这是一种值得借鉴的方法。
参考文献
[1] A Na Varro,M J Nunez,E Martin.Study of Teo and TMo Modes In Dielectric Resonators By A Finite Difference Time-Domain Method Coupled with the Dis-crete Fourier Transform.IEEE Trans.Microwave Theory Tech.,1991,39(1):14~17.
[2] K S Yee.Numerical Solution of Initial Boundary Value Problems Involving Maxwell’s Equations in Isotropic Media.IEEE Trans.Antenna Propagat.,1966,14(5):302~307.
[3] G Mur.Absorbing Boundary Conditions for the Finite Difference Approximation of the Time-Domain Electro-magnetic Field Equations.IEEE Trans.Electromagn.Compat.,1981,23(11):377~382.
[4] D H Choi,W J R Hoefer.The Finite Difference-Time Domin Method and Its Appliaction To Eigenvalue Problems.IEEE Trans.Microwave Theory Tech.,1986,34(12):1464~1469.
[5] M F Catedra,R P Torres,J Basterrechea,E Cago.In the CG-FFT Method:Application of Signal Processing Techniques To Electomagnetics.Artech House,1995.
[6] J Liva,Z Bi,K Wu,R Fralich,C Wu.Full-wave Analysis of an Assortment of aPrinted Antenna Struc-tures Using thd FD-TD method.In:IEEE AP-S Int.Symp.Dig.,1991,(1):410~413

