- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
微波ECR大面积磁场的模拟与设计
录入:edatop.com 点击:
微波ECR大面积磁场的模拟与设计
高旭东 杨银堂
高旭东 杨银堂
(西安电子科技大学微电子研究所 , 西安 , 710071)
摘 要:本文主要研究对ECR大面积磁场的模拟和设计。在了解ECR磁场的构成的基础上,通过模型推理和实测修正得到小磁块的场强分布函数,进而得到叠加磁场的场强分布函数。然后通过编程,用软件实现对ECR大面积磁场的模拟,进一步优化了磁场的设计,证实该磁场可用于实现高质量ECR等离子体源。
关键词:电子回旋共振;磁偶极子;电偶极子;磁场强度
关键词:电子回旋共振;磁偶极子;电偶极子;磁场强度
Simulation and Design of Microwave ECR
Large-area Magnetic Field
GAO Xudong YANG Yintang
Large-area Magnetic Field
GAO Xudong YANG Yintang
(Institute of Microelectronics , Xidian university, Xi’an , 710071,CHN )
Abstract: A simulation and design of ECR magnetic field is presented in this paper. Begin with the structure of ECR magnetic field, we obtain the distributed function of a small magnetic block by model reasoning and modifying ,Furthermore, the distributed function of magnetic field folded. Then ,a software is programed to realize the simulation ,further to optimize the design of magnetic field and to make it sure that this magnetic field can be used to realize the plasma source superior in quality.
Key words: ECR; magnetic monopole; electric monopole; magnetic field intensity
Key words: ECR; magnetic monopole; electric monopole; magnetic field intensity
1 引 言
随着VLSI技术的发展,对于新材料、新工艺的要求更加迫切,微波ECR( Electronic convolution resonance)等离子体因其在没有金属电极、极低气压的情况下有很高的离化率,已被广泛应用于多种材料的刻蚀、淀积、溅射、清洗等工艺过程。与其它等离子体相比较,电子回旋共振(ECR)微波放电产生的等离子体由于密度高(1010~1012-3),电离度大(>10%),工作气压低(1~10-3Pa),均匀性好,工艺设备简单,参数易于控制等优点,可以实现低温高效无污染的表面处理[1]。并且当工作气压低于10-2Pa时,离子能量在20~50ev范围内,减少了衬底受热和离子轰击效应对衬底的损伤[2]。低表面损伤、高刻蚀速率和高选择性对于得到精细的亚微米图形是非常重要的。将其应用于等离子体中,获得了高质量的SiO2、SiN、SiC、Si、α-Si、poly-Si和多晶金刚石等薄膜[3,4]。在溅射镀膜方面得到了ZnO、Ta2O3、Al2O3、Al、Cu、Fe和Mo多种薄膜[5-7]。近几年来,低压下的高密度、高均匀性等离子体源在微电子应用中显得越来越重要。
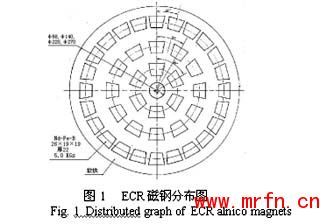
ECR磁场是实现高质量ECR等离子体源的关键因素之一。在2.45GHZ微波功率源的系统中,电子回旋共振需要的磁场是875GS。设计大面积高强度ECR磁场是ECRCVD系统的关键技术难点. 我们设计了利用新型高磁能积块状Nd-Fe-B永磁磁钢通过合理分布而形成的高强磁场。尺寸为20×20×22mm3Nd-Fe-B永磁磁钢的表面磁场强度大约5000GS,在距磁钢表面50mm处形成平面型ECR区。与ECR等离子体源的结构相匹配,设计了环形相间排列的大面积平面分布式ECR磁场。其磁钢排列如图1所示。磁块单元的环型排列,在空间叠加产生了所需的磁场。为了研究它们的叠加磁场,有必要得到磁块单元的磁感应强度的分布函数。
随着VLSI技术的发展,对于新材料、新工艺的要求更加迫切,微波ECR( Electronic convolution resonance)等离子体因其在没有金属电极、极低气压的情况下有很高的离化率,已被广泛应用于多种材料的刻蚀、淀积、溅射、清洗等工艺过程。与其它等离子体相比较,电子回旋共振(ECR)微波放电产生的等离子体由于密度高(1010~1012-3),电离度大(>10%),工作气压低(1~10-3Pa),均匀性好,工艺设备简单,参数易于控制等优点,可以实现低温高效无污染的表面处理[1]。并且当工作气压低于10-2Pa时,离子能量在20~50ev范围内,减少了衬底受热和离子轰击效应对衬底的损伤[2]。低表面损伤、高刻蚀速率和高选择性对于得到精细的亚微米图形是非常重要的。将其应用于等离子体中,获得了高质量的SiO2、SiN、SiC、Si、α-Si、poly-Si和多晶金刚石等薄膜[3,4]。在溅射镀膜方面得到了ZnO、Ta2O3、Al2O3、Al、Cu、Fe和Mo多种薄膜[5-7]。近几年来,低压下的高密度、高均匀性等离子体源在微电子应用中显得越来越重要。
ECR磁场是实现高质量ECR等离子体源的关键因素之一。在2.45GHZ微波功率源的系统中,电子回旋共振需要的磁场是875GS。设计大面积高强度ECR磁场是ECRCVD系统的关键技术难点. 我们设计了利用新型高磁能积块状Nd-Fe-B永磁磁钢通过合理分布而形成的高强磁场。尺寸为20×20×22mm3Nd-Fe-B永磁磁钢的表面磁场强度大约5000GS,在距磁钢表面50mm处形成平面型ECR区。与ECR等离子体源的结构相匹配,设计了环形相间排列的大面积平面分布式ECR磁场。其磁钢排列如图1所示。磁块单元的环型排列,在空间叠加产生了所需的磁场。为了研究它们的叠加磁场,有必要得到磁块单元的磁感应强度的分布函数。
2 永久磁铁的磁荷模型
磁荷模型的基本思想是用假想磁荷来解释磁场产生的机理,并结合电荷和电场的相关思想推导出在各种边界条件下的磁荷与场强的关系表达式。
我们知道,电荷分别为、彼此相距为l的一对电荷,共同组成一个电偶极子(如图2)。
磁荷模型的基本思想是用假想磁荷来解释磁场产生的机理,并结合电荷和电场的相关思想推导出在各种边界条件下的磁荷与场强的关系表达式。
我们知道,电荷分别为、彼此相距为l的一对电荷,共同组成一个电偶极子(如图2)。
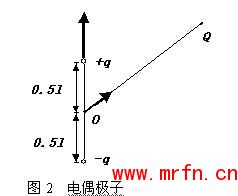
它产生的电矩为:P=ql
其中向量l的方向是由-q到+q。这个电偶极子在介电常数为ε0Q产生的电位为:
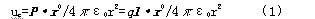
的空间内任意一点式中 r——由电偶极子中心O至Q点的距离;
r0——沿r的单位向量;
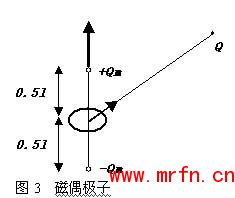
同样,一个磁矩为m的分子电流,在磁导率为µ0的介质空间内任意一点Q(图3)产生的标量磁位为:

其中向量l的方向是由-q到+q。这个电偶极子在介电常数为ε0Q产生的电位为:
的空间内任意一点式中 r——由电偶极子中心O至Q点的距离;
r0——沿r的单位向量;
同样,一个磁矩为m的分子电流,在磁导率为µ0的介质空间内任意一点Q(图3)产生的标量磁位为:

上式便是磁荷产生的磁位分布函数。
得到了磁位的表达式后,对其求梯度便可得到磁感应强度的函数表达式:
得到了磁位的表达式后,对其求梯度便可得到磁感应强度的函数表达式:
以假想磁荷的概念分析磁化物质,是将磁化物质看作一个充满磁偶极子的"真空"空间。结合永久磁铁的特有性质和其充磁方向,经分析可得到如下结论:
任意等截面永磁直棒,如图(4)
任意等截面永磁直棒,如图(4)
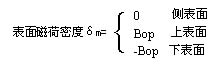
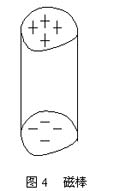
体内磁荷密度ρm=0,磁块上下表面均匀分布有正负磁荷。其中 Bop为表面磁感应强度。
实际应用中磁单元形状为:
实际应用中磁单元形状为:
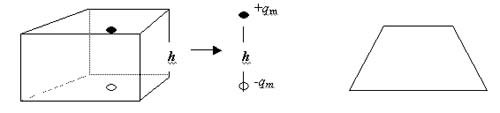
所以完全可以采用上述模型。
通过前面的分析,可用磁荷和磁偶极子来分析梯形体磁块。
将上下表面分割为无数磁偶极子,通过积分便可得到磁块在空间的磁位分布,然后通过梯度可得到磁感应强度B分布函数!
假设所有磁荷均集中于梯形中心,上下对称形成一磁偶极子,简化引起的误差我们通过实测值进行修正。
已知磁偶极子的磁位公式如式(2):
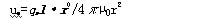
我们将通过这个公式得到基本的磁感应强度分布函数。
下面建立三维坐标系(图5)
通过前面的分析,可用磁荷和磁偶极子来分析梯形体磁块。
将上下表面分割为无数磁偶极子,通过积分便可得到磁块在空间的磁位分布,然后通过梯度可得到磁感应强度B分布函数!
假设所有磁荷均集中于梯形中心,上下对称形成一磁偶极子,简化引起的误差我们通过实测值进行修正。
已知磁偶极子的磁位公式如式(2):
我们将通过这个公式得到基本的磁感应强度分布函数。
下面建立三维坐标系(图5)
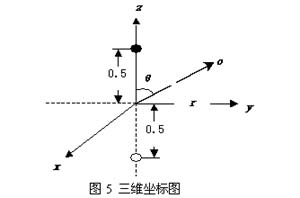



对于实际的梯形磁块有:
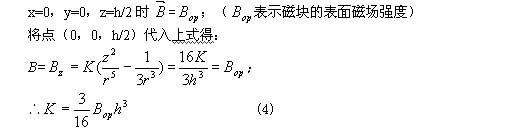
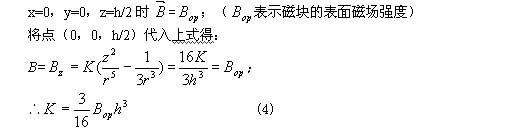
此系数可由磁块高度和表面磁场强度得到。至此,已经得到了一个基本的场强分布函数。
3 分布函数的修正
根据前面的结果,将计算值和实测值比较,在各个方向上的趋势完全一致,其趋势和峰谷都可以较好的吻合,只是陡缓高低有差别.由于模型本身的合理性,使得计算结果与实际场强相差呈现规律性。将实测值比上计算值,其比例值呈现为缓慢上升的指数形势,因此可以通过指数形式的修正函数来修正它们。
首先修正Bz。选择一个较合理的指数,使得与实际的Bz值相差不大,这可以通过观察得到。选好以后,肯定在某些地方表现差异较大,若偏小则修正指数要变大,若偏大这修正指数要变小,结合高度调整指数的大小,仔细观察几次便可得到较好的修正结果。
根据前面的结果,将计算值和实测值比较,在各个方向上的趋势完全一致,其趋势和峰谷都可以较好的吻合,只是陡缓高低有差别.由于模型本身的合理性,使得计算结果与实际场强相差呈现规律性。将实测值比上计算值,其比例值呈现为缓慢上升的指数形势,因此可以通过指数形式的修正函数来修正它们。
首先修正Bz。选择一个较合理的指数,使得与实际的Bz值相差不大,这可以通过观察得到。选好以后,肯定在某些地方表现差异较大,若偏小则修正指数要变大,若偏大这修正指数要变小,结合高度调整指数的大小,仔细观察几次便可得到较好的修正结果。
利用上面的修正函数,x=0,y=0,z:0----60时 修正Bz的结果如图所示。
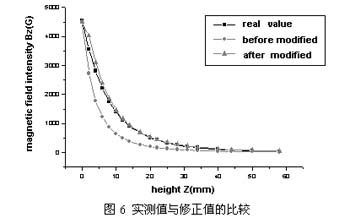
同样的思路可以得到Bx,By的修正函数:
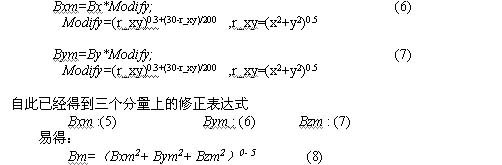
通过计算值与实测值的比较,我们可以发现,修正结果比较符合实际的测量值。因此,我们可以用修正函数来表示是磁块场强的分布。
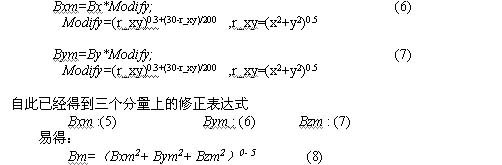
通过计算值与实测值的比较,我们可以发现,修正结果比较符合实际的测量值。因此,我们可以用修正函数来表示是磁块场强的分布。
4 程序设计
用得到的修正分布函数,通过编制程序,可较准确的模拟ECR大面积磁场的场强分布。可以计算空间内任意一点的场强,计算给定场强所处的高度;图形显示空间任意水平层面和垂直切面的场强分布示意图;曲线显示水平层面内任意径向上的场强大小,并且列出具体的数值;计算任一高度层面的场强平均值、均方差;求得任意均值场强所在的高度。也可设计新的磁场进行模拟,如改变磁块的排列方式﹑个数﹑极性和高度。
程序编制的关键是利用已得到的场强分布函数,建立统一坐标系,计算众多磁偶极子在空间同一点产生的叠加场强。该模拟程序用Visual C++语言完成。
用得到的修正分布函数,通过编制程序,可较准确的模拟ECR大面积磁场的场强分布。可以计算空间内任意一点的场强,计算给定场强所处的高度;图形显示空间任意水平层面和垂直切面的场强分布示意图;曲线显示水平层面内任意径向上的场强大小,并且列出具体的数值;计算任一高度层面的场强平均值、均方差;求得任意均值场强所在的高度。也可设计新的磁场进行模拟,如改变磁块的排列方式﹑个数﹑极性和高度。
程序编制的关键是利用已得到的场强分布函数,建立统一坐标系,计算众多磁偶极子在空间同一点产生的叠加场强。该模拟程序用Visual C++语言完成。
5 模拟结果
磁钢分布如图1所示,程序得到的部分模拟结果如下:磁场沿径向的分布如图7所示;在0-30mm高度内,各层面的场强均值分布如图8;距离磁钢表面8cm的磁场强度三维分布如图9。
磁钢分布如图1所示,程序得到的部分模拟结果如下:磁场沿径向的分布如图7所示;在0-30mm高度内,各层面的场强均值分布如图8;距离磁钢表面8cm的磁场强度三维分布如图9。
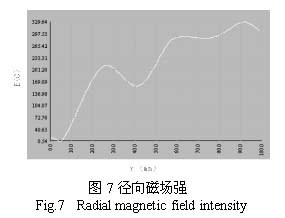
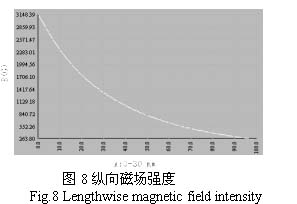
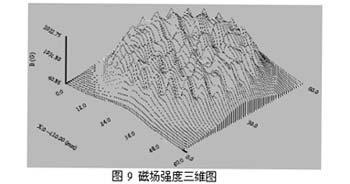
层面高度分别取4毫米、19毫米、22毫米,模拟层面平均值的误差分别为6.96%、5.50%、0.2%。误差基本上在10%以内,而且高度越高,误差越小。
由以上结果分析可知,所以,本模拟程序对叠加磁场的层面均值的模拟具有一定的正确性。
层面高度:22毫米,旋转角度:0度,如下。
由以上结果分析可知,所以,本模拟程序对叠加磁场的层面均值的模拟具有一定的正确性。
层面高度:22毫米,旋转角度:0度,如下。
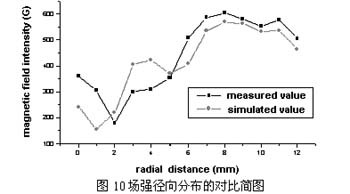
通过上图对比可知,在径向上的分布,大致相同,有对应的峰和谷,径向距离越远,层面越高吻合程度越好。
6 结论
本文首先研究了永久磁铁的磁荷模型,利用它得到一个基本的磁感应强度的分布函数。然后在此基础之上,结合实际的测量值,对比理论值和实测值发现规律然后进行修正。然后通过编程,用软件实现对ECR大面积磁场的模拟,并得到了较好的模拟效果,根据模拟结果,进一步优化ECR磁场系统,设计出了由Nd-Fe-B永磁磁钢组成的磁场系统(图1)和ECR刻蚀系统。永磁分布型等离子体源具有面积大、均匀性好、结构紧凑、体积小、价格低等优点。20×20×22mm Nd-Fe-B永磁磁钢表面磁场强度大于3000Gs,由此在距磁钢表面50mm处形成平面型ECR区,在此磁场和由微波形成的电场的作用下,可产生密度在1010~1012-3的高质量等离子体。
本文首先研究了永久磁铁的磁荷模型,利用它得到一个基本的磁感应强度的分布函数。然后在此基础之上,结合实际的测量值,对比理论值和实测值发现规律然后进行修正。然后通过编程,用软件实现对ECR大面积磁场的模拟,并得到了较好的模拟效果,根据模拟结果,进一步优化ECR磁场系统,设计出了由Nd-Fe-B永磁磁钢组成的磁场系统(图1)和ECR刻蚀系统。永磁分布型等离子体源具有面积大、均匀性好、结构紧凑、体积小、价格低等优点。20×20×22mm Nd-Fe-B永磁磁钢表面磁场强度大于3000Gs,由此在距磁钢表面50mm处形成平面型ECR区,在此磁场和由微波形成的电场的作用下,可产生密度在1010~1012-3的高质量等离子体。
参考文献
[1] 孙剑,吴嘉达等,半导体学报,2000,21(10):19 ~ 23 [2] Toshiro Ono, et al. Reactive Ion Stream Etching Utilizing Electron Cyclotron Resonance Plasma[J]. J Vac Sci Technol, 1986, B4 (3): 696
[3] Seitaro Matsuo, Mikiho Kiuchi, Low Temperature Chemical Vapor Deposition Method Utilizing an ECR Plasma[J]. Jpn J Appl Phys, 1983, 22, 210
[4] Knox R D, et al. Amorphous and Polycrystalline Silicon Films Deposited by ECR Reactive Plasma Deposition[J]. J Appl Phys, 1993, All (4): 1896
[5] Michio Kadota, et al. Characteristics of Zinc Oxide Films on Glass Substrates Deposited by RF-Mode ECR Sputtering System[J].Jpn J Apply Phys, 1993, 32: 2341
[6] Morito Matsuoka, Ken’ chi Ono. A Few Techniques for Preparing Conductive Material Films for Sputtering-Type ECR Microwave Plasma[J].1989, 28: 503
[7] Toshiro Ono, et al. ECR Plasma Deposition Technique using Raw Material Supply by Sputtering[J]. Jpn J Appl Phys, 1984, 23: 534
[8] 4P.Silvester,’Computation of Magnetostatic Fields[A],Proc.COMPUMAG,Oxford,1976.
[9] S.J.Polak, A de Beer , A.Wachters and J. S.van Welij,‘MAGGY2’,A Program Package of Two Dimensional Magneto static Problems[J],Int.J.Num.Meth.Ergng., Vol.15, No.1, 1980
[3] Seitaro Matsuo, Mikiho Kiuchi, Low Temperature Chemical Vapor Deposition Method Utilizing an ECR Plasma[J]. Jpn J Appl Phys, 1983, 22, 210
[4] Knox R D, et al. Amorphous and Polycrystalline Silicon Films Deposited by ECR Reactive Plasma Deposition[J]. J Appl Phys, 1993, All (4): 1896
[5] Michio Kadota, et al. Characteristics of Zinc Oxide Films on Glass Substrates Deposited by RF-Mode ECR Sputtering System[J].Jpn J Apply Phys, 1993, 32: 2341
[6] Morito Matsuoka, Ken’ chi Ono. A Few Techniques for Preparing Conductive Material Films for Sputtering-Type ECR Microwave Plasma[J].1989, 28: 503
[7] Toshiro Ono, et al. ECR Plasma Deposition Technique using Raw Material Supply by Sputtering[J]. Jpn J Appl Phys, 1984, 23: 534
[8] 4P.Silvester,’Computation of Magnetostatic Fields[A],Proc.COMPUMAG,Oxford,1976.
[9] S.J.Polak, A de Beer , A.Wachters and J. S.van Welij,‘MAGGY2’,A Program Package of Two Dimensional Magneto static Problems[J],Int.J.Num.Meth.Ergng., Vol.15, No.1, 1980

