- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
高电容比射频/微波MEMS膜开关理论分析和数值模拟
录入：edatop.com 点击：
高电容比射频/微波MEMS膜开关理论分析和数值模拟*
龙永福1，2，赖宗声1，朱自强1
（1.华东师范大学电子系，上海 200062；2.常德师范学院物电系，常德 415000）
摘 要：建立了一个MEMS膜开关电容比理论模型。由于这个模型比较全面地考虑了开关阈值电压、维持电压、偏置电压和介质膜内的电场强度等因素对电容比的影响，因而能较为正确地反映开关的电容特性。用数值方法计算了影响开关电容比的因素，并对计算结果进行了分析和讨论。提出了使用脉冲电压作为偏置电压可以使介质膜gi的厚度减少到50nm，从而使开关的电容比增加到3800。最后，讨论了实现高电容比MEMS膜开关的可行性。
关键词：MEMS膜开关，电容比，阈值电压，维持电压
1 引言
近40年来，开关作为信号变换的关键器件之一，在射频/微波集成电路中已经大量使用FET和PIN等半导体管开关。由于这类开关具有较低的工作频率、较大的插入损耗、较低的隔离度及其固有的非线性特性，导致半导体开关存在许多缺陷。近10年来，随着微电子技术的飞速发展，出现了微机电系统（MEMS，Micro-Elecgtro-Mechanical Systems）技术。人们可将微电子元件和微机械元件结合在一起构成了微型化器件和器件阵列。MEMS开关作为射频/微波电路中的最基本的信号变换元件，已经是一种获得广泛研究的器件[1，2]。MEMS开关与传统的p-i-n二极管开关及FET开关相比，由于消除了p-n结和金属-半导体结，也消除了由于半导体结引起的I-V非线性，因而显著地减少了开关的谐波分量和互调分量。MEMS膜开关[3，4]通过在信号一和可支桥之间添加一层绝缘介质，可以减少静摩擦力且消除了微连接，从而提高了开关的稳定性和电性能。由于不需直流电流驱动，静电驱动MEMS膜开关仅需少的瞬间能量，其典型值大约是10nJ。典型MEMS膜开关的插入损耗随信号频率的增加而增加，从小于01dB(1GHz)增加到0.25dB(40GHz)；隔离度随信号频率的增加而减少，从40dB(40GHz)[5]。因此，MEMS膜开关是半导体开关较好的替代品，且已经作为射频/微波无源器件应用到了微波电路中，如微开关、微相移器、微振荡器和微相控阵列天线等。MEMS膜开关的插入损耗和隔离度与开关在导通和截止时的耦合电容比值大小有关。为了减少开关导通时的插入损耗，开关在‘开’态时的耦合电容Con应尽可能小；而为了提高开关在断开时的隔离度，‘关’态时的耦合电容Coff应尽可能大。这样，MEMS膜开关的电容比值Coff/Con是开关性能特性的关键参数之一。据文献报道，现有开关的电容比通常为30～80。而要较大幅度地增加开关的电容比值Coff/Con，瓶颈是：在开关的整个开启时间内，所加的偏置电压为矩形信号Vp，当介质膜的厚度小于100nm时，氮化硅介质膜会电击穿[5]，从而导致开关不稳定或失效。
本文提出将外加偏置电压Vbias改为脉冲电压，并降低绝缘介质膜的厚度，则开关的电容比Coff/Con可能增加，且不会导致介质膜电击穿，从而极大地提高MEMS开关及其衍生器件的性能。
2 基本理论
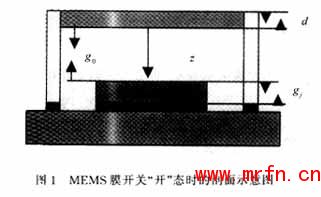
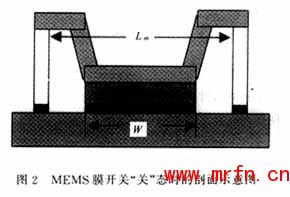
MEMS膜开关的结构示意图如图1、2所示。在外加偏置电压的作用下，可动桥向介质层移动。MEMS膜开关在运行过程中，必须确保在最小外加偏置电压的作用下，绝缘介质膜不被电击穿，而能得到开关的最大电容比，从而提高开关的性能。本文从理论上分析了影响MEMS膜开关电容比的因素，并数值分析了高电容比开关实现的可行性。
2.1 阈值电压
典型MEMS膜开关的示意图及其结构参数如图1、2所示。为了开启MEMS开关，CPW中间传输线与可动桥之间必须加直流电压。可动桥在静电力拖动下向介质层移动，共有两个力（忽略空气的阻力）作用在可动桥上。第一个力为静电力Fe，它是由偏置电压Vbias产生，其大小由有关的电学知识可得：
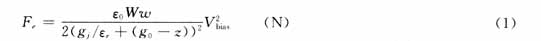
其次是可动桥受到的弹力，其大小为：
其中z为可动桥离开平衡位置的位移。
其中z为可动桥离开平衡位置的位移。
为了将可动桥拉下，静电力必须大于可动桥受到的弹力，其阈值电压Vp[5]为：
其中ε0
Y为可动桥材料的场氏模量，d为可动桥的厚度，Lm为可动桥的长度，δ为桥材料内部残存的张应力，γ为桥材料的泊松比。为真空介电常数，W为共面波导（CPW）中间传输导体的宽度，w为可动桥的宽度，g0为可动桥离介质层上表面的标称高度，k为系统可动总值发的有效弹性系数，且由文献[6]可得：
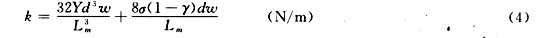
其中ε0
Y为可动桥材料的场氏模量，d为可动桥的厚度，Lm为可动桥的长度，δ为桥材料内部残存的张应力，γ为桥材料的泊松比。为真空介电常数，W为共面波导（CPW）中间传输导体的宽度，w为可动桥的宽度，g0为可动桥离介质层上表面的标称高度，k为系统可动总值发的有效弹性系数，且由文献[6]可得：
2.2 维持电压
当可动桥被拉下后，开关断开。为了维持开关断开状态，作用在可动桥上的静电力必须大于或等于其弹性恢复力（忽略表面分子间的范德华力和液体的表面张力（如果有水分的话）），否则，可动桥被弹起。通过建立静电力和其弹性恢复力两力平衡方程，可以由公式（1）、（2）求得其维持电压Vw,其大小为：
公式（5）为MEMS膜开关维持"关"态所需要的最小偏置电压。
公式（5）为MEMS膜开关维持"关"态所需要的最小偏置电压。
2.3 电容比
MEMS膜开关的电容比是衡量MEMS膜开关性能的重要特性之一。理想情况下要求开关在"开"态时的电容值为零，而在"关"态时的电容值为无穷大。如图1、2所示，MEMS膜开关的总电容是由可动桥下表面与介质层上表面之间的空气层所构成的电容Cair和介质膜层的电容Cj串联组成。当偏置电压Vbias加在可动桥与CPW中间传输线上时，静电力拖动可动桥向介质层移动。在可动桥小形变的情况下，可动桥与介质层之间的空气层电容Cair可近似为一可变平行板电容器[5]，其大小随可动桥离开平衡位置的位移z而变化，且其大小Cair可表示为：
当MEMS膜开关处于"关"态或激活时，"关"态电容仅仅由介质层组成，也可以近似看成平行板电容器，且可以用下列公式计算：
同时，当开关处于"开"态或未被激活时，"开"态的电容Con由介质层电容Cj和空气层的电容Cair串联而成，且可由下式计算：
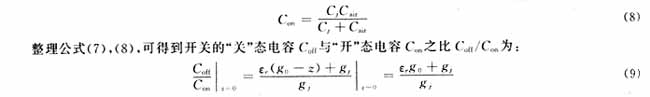
当MEMS膜开关处于"关"态或激活时，"关"态电容仅仅由介质层组成，也可以近似看成平行板电容器，且可以用下列公式计算：
同时，当开关处于"开"态或未被激活时，"开"态的电容Con由介质层电容Cj和空气层的电容Cair串联而成，且可由下式计算：
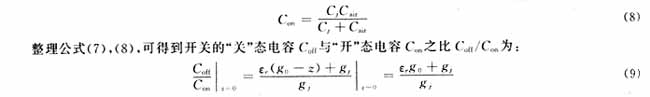
其中εr为介质膜的相对介电常数。
由公式（9）可知，要增大开关的电容比，可以减少gi，增加g0或增加介质的相对介电常数εr。
2.4 介质膜内的电场强度
为了确保MEMS膜开关在"开"和"关"过程中运行稳定，要求介质膜内的电场强度不能大于或长时间在介质的击穿电场附近工作。据文献[5]报道，限制MEMS膜开关电容比较低的原因是：如果介质膜gj太薄，在外加偏置电压的作用下，开关在动作过程中，介质膜内的电场强度有可能大于介质的介电强度（击穿电场）或长期在介质的击穿电场附近工作，从而导致开关工作不稳定或过早失效。在偏置电压的作用下，偏置电压加在两串联电容Cair、Cj上。可动桥在移动过程中，介质膜内的电场强度可以表示为：
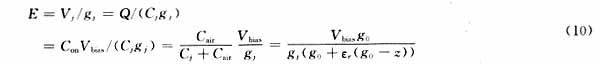
由（6）、（10）式，当可动桥从平衡位置向介质膜运动时，Cair的电容逐步增加，偏置电压Vbias逐渐加在介质膜上，从而使介质膜内的电场强度逐步增大。
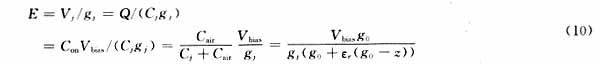
由（6）、（10）式，当可动桥从平衡位置向介质膜运动时，Cair的电容逐步增加，偏置电压Vbias逐渐加在介质膜上，从而使介质膜内的电场强度逐步增大。
3 数值结果
为了分析MEMS膜开关的电容特性，研究了在不同偏置电压的作用下，不使介质膜电击穿的条件下，开关"关"态与"开"的电容比与介质膜的厚度和偏置电压等因素之间的关系。根据目前已经检索的文献[2-4]报道，启动MEMS膜开关的偏置电压均是矩形波信号，且其幅度为阈值电压。使用矩形波信号、正弦波信号和脉冲波信号等3种信号作为偏置电压，对MEMS膜开关的电容比变化规律进行了数值分析。为了研究MEMS膜开关的电容比Coff/Con与偏置电压之间的关系，使不同偏置电压作用下数值计算结果具有可比性，在具体的计算中，开关的结构参数采用文献[4]中的典型值。组成可动桥的材料为Au，其详细的输入波形图、器件结构参数及数值计算结果如图（3）～（7）所示。
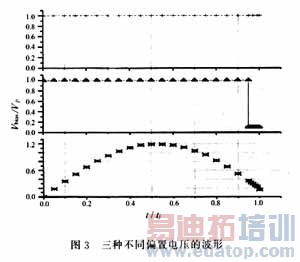
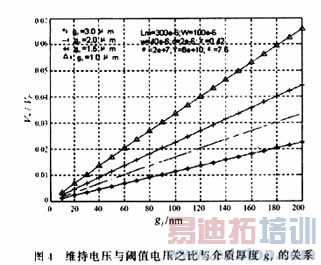
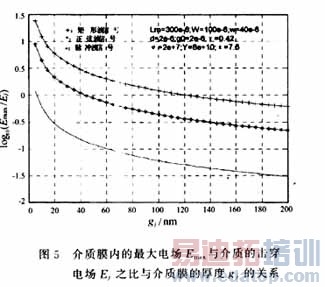
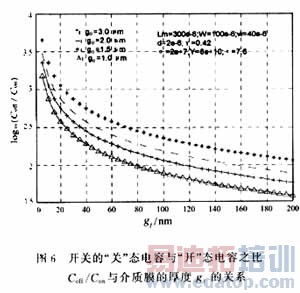
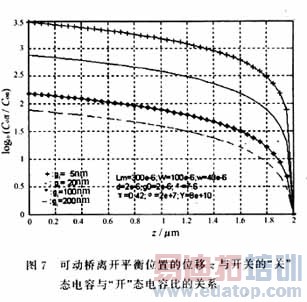
4 结论
本文就MEMS膜开关的重要特性—电容比进行了详细的理论分析和数值计算，得出了在开关的材料、结构参数基本不变的情况下，通过改变天关的偏置电压Vbias改变了开关"关"态和"开"态的电容比。在本文的研究中，没有考虑可动桥与介质膜之间的非弹性碰撞对开关维持电压产生的影响。由于开关的材料及结构参数（除gj之外）均未变化，因此开关的性能如阈值电压、开启时间等均变化不大（本文未讨论）。研究结果表明：使用脉冲电压作偏置电压时，可以将介质膜的厚度降低到5nm左右，而该厚度基本上达到了介质膜的粗糙度，达到了介质膜的最小厚度极限[5]，开关的电容比可达3800，因而将极大地改善MEMS膜开关的插入损耗和隔离度等参数。本文的研究结论为提高MEMS膜开关及其衍生器件的性能提供了一条新途径。
参考文献
[1] Yao J J,Chang,M F,A surfac micromachined minia-ture swich for telecommunications applications whth signal frequencies from DC up to 4 GHz.In:int Conf Solid-State Sensors and Actuators,Dig,Stockholm,sweden,June 1995:384～387.
[2] Goldsmith C,Randall J,et al.Characteristics of mi-cromachined switches at microwave frequencies.In:IEEE MTT-Sint Microwave Symp Dig,San Francis-co,CA.June 1996:1141～1144.
[3] Park J Y,Geun H K,et al.Monolithically integrated micromachined RF MEMS Capacitive switches.Sen-sors and Actuators A.,2001,89(5):88～94.
[4] Muldavin J B,Rebeiz G M.High-Isolation MEMS shunt switches-Part 2:Design.IEEE Trans Micro-wave Theory Tech.2000,48(6):1053～1056.
[5] Muldavin J B, Rebeiz G M.High-Isolation MEMS shunt switches-Part1:Modeling,IEEE Trans Micro-wave Theory Tech.2000,48(6):1045～1052.
[6] Osterberg P,Yie H,et al.Self-consistent Simulation and modeling of electrostatically deformed diqphragms.Proc IEEE MEMS Conf.,Jan,1994:28～32.
如何成为一名优秀的射频工程师，敬请关注: 射频工程师养成培训
上一篇：高山微波站的防雷
下一篇：LRL校准法及其在微波测量中的应用
闂傚倸鍊搁崐鎼佸磹閹间礁纾归柟闂寸绾惧湱鈧懓瀚崳纾嬨亹閹烘垹鍊炲銈嗗笒椤︿即寮查鍫熷仭婵犲﹤鍟扮粻缁橆殽閻愭潙鐏村┑顔瑰亾闂侀潧鐗嗛幊鎰版偪閳ь剚淇婇悙顏勨偓鏍涙担鑲濇盯宕熼浣稿妳婵犵數濮村ú锕傚煕閹寸姵鍠愰柣妤€鐗嗙粭鎺懨瑰⿰鈧崡鎶藉蓟濞戙垺鍋愰柛鎰级鐠囩偤鎮楃憴鍕闁搞劌娼￠悰顔碱潨閳ь剟鐛崶銊﹀闁荤喐婢橀崢鐐测攽閿涘嫬浜奸柛濠冪墵瀹曟繈骞嬮敃鈧崹鍌炴煕閿旇骞橀柣顓炵墛閵囧嫰寮村Δ鈧禍鎯р攽椤旂》鏀绘俊鐐舵铻為柛鎰╁妷濡插牊绻涢崱妯曟垿藟閿濆鈷掑ù锝呮嚈瑜版帗鏅濋柕鍫濐槴閳ь剨绠撻幃婊堟偩鐏炵晫銈﹂梻浣侯攰閹活亞绮婚幋鐘电焼閻庯綆鍋佹禍婊堟煙閻戞ê鐏ラ柍褜鍓欓…鐑界嵁婵犲倵鏀介柛鈾€鏅滅€靛矂姊洪棃娑氬婵☆偅绋掗弲鍫曨敆閸屾粍锛忛梺鍝勵槼濞夋洖鐡梻浣哥枃椤曆呯矓閻㈠灚宕叉繝闈涱儏閻愬﹪鏌曟繛鍨仾閻庢俺妫勯埞鎴︽倷鐎涙ê闉嶉梺绯曟櫅閸熸潙鐣烽幋锕€绠婚悗闈涙憸椤旀洘绻涙潏鍓у埌闁哥喎鐏濈叅闁挎洖鍊搁悿鐐亜閹烘垵顏柛娆愭崌閺屾盯濡烽敐鍛瀷闂佸疇妫勯ˇ鐢稿蓟閿濆绠抽柟瀵稿С缁敻姊洪棃娑欐悙閻庢矮鍗抽悰顕€骞掑Δ鈧粻锝嗙節閸偄濮冮柟顕嗙秮濮婄粯鎷呴懞銉闂佸摜鍠嶉崡鍐茬暦娴兼潙鍐€妞ゆ挾鍋犻幗鏇㈡⒑閸濆嫭鍌ㄩ柛銊ョ秺閺屽宕堕妸褏鐦堥梺鍓茬厛閸嬪嫭鎱ㄩ崼銉ユ瀬闁割偁鍎查埛鎺懨归敐鍛殘鐟滅増甯╅弫鍕煕閹伴潧鏋涚紒鈧径灞稿亾楠炲灝鍔氭い锔诲灡椤㈠﹪姊绘担鍛婂暈婵炶绠撳畷瑙勫閺夋垹顦ㄩ梺閫炲苯澧存慨濠冩そ濡啫鈽夐幒鎴炲€ｅ┑鐘殿暯閳ь剝娅曢幖鎰版煃缂佹ɑ宕屽┑鈥崇埣瀹曞崬鈻庨幋鐘愁潓闂傚倷绀侀崯鍧楁儍濠靛纾婚柟鍓х帛閻撴洟鏌￠崶銉ュ濠⒀呭閵囧嫰鏁傞崹顔肩ギ濠殿喖锕ュ钘夌暦椤愶箑绀嬫い鎾跺Т婵晫绱撻崒姘偓鍝ョ矓瀹曞洦顐芥慨妯垮煐閸嬫ɑ銇勯弬鎸庮潔闁绘梻鍘х粈鍌炴煟閹惧啿顒㈤柣搴弮濮婄粯鎷呴崨濠傛殘濠电偠顕滅粻鎾崇暦閵忥絻浜归柟鐑樺灩閸旓箑顪冮妶鍡楀潑闁稿鎹囬弻銊╁即閵娿倗鐩庡銈庡亜缁绘劗鍙呭銈呯箰閹冲孩绂掗銏♀拺闁告繂瀚峰Σ褰掓倵缁楁稑鍊婚弰鍌涚節绾板纾块柛瀣灴瀹曟劙寮介鐐茬€梺姹囧灪濞煎矂宕堕浣镐缓缂備礁顑堥鎶藉Ψ閵夊啫缍婇弫鎰板川椤撗勵棏婵犵數鍋熼鏇㈠礉閹达箑钃熺€广儱鐗滃銊╂⒑閸涘﹥灏甸柛鐘崇墵閹即顢氶埀顒€鐣峰鈧、娆戝枈鏉堛劎绉遍梻鍌欑窔濞佳囨偋閸℃稑绠犻幖杈剧悼閻滅粯绻涢幋鐐垫噮缂佲檧鍋撻梻浣圭湽閸ㄨ棄岣胯閻☆參姊虹拠鎻掝劉闁告垵缍婂畷銏＄附缁嬭法鍘洪梺鍦亾濡炲潡寮繝鍥ㄧ厱闁圭偓顨呴幏鎴犳閹惰姤鈷掑ù锝呮嚈瑜版帒瀚夋い鎺戝閸ゅ苯螖閿濆懎鏆欓柣鎺戠仛閵囧嫰骞掗幋婵愪紝濠碘槅鍋呴崹鍦閹烘鏁婇柤娴嬫櫅椤も偓缂傚倷鐒﹂〃鍫ュ窗閺嶎厼鏄ラ柍褜鍓氶妵鍕箳閹存繍浠撮梺閫炲苯鍘哥紒鑸佃壘椤曪絾绂掔€ｅ灚鏅ｉ梺缁樺姈椤旀牠宕ラ崨瀛樷拻濞达絿鎳撻婊勭箾閹绘帞效鐎规洘鍨块獮姗€宕滄担鐚寸床闂備胶绮悷銏ゅ磻閹剧粯鐓曢柕濞垮劤閸╋絿鈧鍠栭…閿嬩繆閹间礁鐓涢柛灞剧煯缁ㄤ粙姊绘担鍛靛綊寮甸鍌滅煓闁硅揪瀵岄弫鍌炴煥閻曞倹瀚� | More...
闂傚倸鍊搁崐鎼佸磹閹间礁纾归柟闂寸绾惧湱鈧懓瀚崳纾嬨亹閹烘垹鍊炲銈嗗笒椤︿即寮查鍫熷仭婵犲﹤鍟扮粻缁橆殽閻愭潙鐏村┑顔瑰亾闂侀潧鐗嗛幊鎰版偪閳ь剚淇婇悙顏勨偓鏍涙担鑲濇盯宕熼浣稿妳婵犵數濮村ú锕傚煕閹寸姵鍠愰柣妤€鐗嗙粭鎺懨瑰⿰鈧崡鎶藉蓟濞戙垺鍋愰柛鎰级鐠囩偤鎮楃憴鍕闁搞劌娼￠悰顔碱潨閳ь剟鐛崶銊﹀闁荤喐婢橀崢鐐测攽閿涘嫬浜奸柛濠冪墵瀹曟繈骞嬮敃鈧崹鍌炴煕閿旇骞橀柣顓炵墛閵囧嫰寮村Δ鈧禍鎯р攽椤旂》鏀绘俊鐐舵铻為柛鎰╁妷濡插牊绻涢崱妯曟垿藟閿濆鈷掑ù锝呮嚈瑜版帗鏅濋柕鍫濐槴閳ь剨绠撻幃婊堟偩鐏炵晫銈﹂梻浣侯攰閹活亞绮婚幋鐘电焼閻庯綆鍋佹禍婊堟煙閻戞ê鐏ラ柍褜鍓欓…鐑界嵁婵犲倵鏀介柛鈾€鏅滅€靛矂姊洪棃娑氬婵☆偅绋掗弲鍫曨敆閸屾粍锛忛梺鍝勵槼濞夋洖鐡梻浣哥枃椤曆呯矓閻㈠灚宕叉繝闈涱儏閻愬﹪鏌曟繛鍨仾閻庢俺妫勯埞鎴︽倷鐎涙ê闉嶉梺绯曟櫅閸熸潙鐣烽幋锕€绠婚悗闈涙憸椤旀洘绻涙潏鍓у埌闁哥喎鐏濈叅闁挎洖鍊搁悿鐐亜閹烘垵顏柛娆愭崌閺屾盯濡烽敐鍛瀷闂佸疇妫勯ˇ鐢稿蓟閿濆绠抽柟瀵稿С缁敻姊洪棃娑欐悙閻庢矮鍗抽悰顕€骞掑Δ鈧粻锝嗙節閸偄濮冮柟顕嗙秮濮婄粯鎷呴懞銉闂佸摜鍠嶉崡鍐茬暦娴兼潙鍐€妞ゆ挾鍋犻幗鏇㈡⒑閸濆嫭鍌ㄩ柛銊ョ秺閺屽宕堕妸褏鐦堥梺鍓茬厛閸嬪嫭鎱ㄩ崼銉ユ瀬闁割偁鍎查埛鎺懨归敐鍛殘鐟滅増甯╅弫鍕煕閹伴潧鏋涚紒鈧径灞稿亾楠炲灝鍔氭い锔诲灡椤㈠﹪姊绘担鍛婂暈婵炶绠撳畷瑙勫閺夋垹顦ㄩ梺閫炲苯澧存慨濠冩そ濡啫鈽夋潏銊愩倝姊虹粙鍨槰闁革綇绲介悾鐑藉箣閿曗偓缁犲鎮归崶銊ョ祷闁哥偑鍔岄—鍐Χ閸℃顫庨梺鍝ュТ鐎涒晝绮嬪澶嬪€锋い鎺嶇瀵灝鈹戦埥鍡楃仯闁告鍕洸濡わ絽鍟崐鍨叏濡厧浜鹃悗姘炬嫹婵犵數濮烽弫鍛婃叏閻戣棄鏋侀柛娑橈攻閸欏繘鏌ｉ幋锝嗩棄闁哄绶氶弻鐔兼⒒鐎靛壊妲紒鐐劤椤兘寮婚敐澶婄疀妞ゆ帊鐒﹂崕鎾绘⒑閹肩偛濡奸柛濠傛健瀵鈽夐姀鈺傛櫇闂佹寧绻傚Λ娑⑺囬妷褏纾藉ù锝呮惈瀛濈紓鍌氱Т閿曨亜顕ｇ拠宸悑濠㈣泛锕ｇ槐鍫曟⒑閸涘﹥澶勯柛鎾寸懃閳诲秹鏁愭径瀣ф嫼缂備礁顑堥崕濠氾綖閿曞倹鐓曢柡鍐ｅ亾闁搞劌鐏濋锝嗙節濮橆厽娅滄繝銏ｆ硾閿曪箓鎮块埀顒勬⒒閸屾艾鈧悂鎮ф繝鍕煓闁硅揪绠戦悡鏇㈡煙閻戞ê鐏嶉柡鈧禒瀣厽闁归偊鍨伴惃鍝勵熆瑜庡鑽ゆ閹烘鏁婇柣锝呮湰閸ｄ即鎮楀▓鍨灈妞ゎ參鏀辨穱濠囧箹娴ｅ摜鍘搁梺绋挎湰閻喚鑺辨禒瀣拻濞达絽鎳欒ぐ鎺戝珘妞ゆ帒鍊婚惌娆撴煙鏉堟儳鐦滈柡浣稿€块弻銊╂偆閸屾稑顏�闂傚倸鍊搁崐鎼佸磹閹间礁纾归柟闂寸绾惧綊鏌熼梻瀵割槮缁炬儳缍婇弻锝夊箣閿濆憛鎾绘煕閵堝懎顏柡灞剧洴楠炴﹢鎳犻鈧俊浠嬫⒑缁嬭法绠茬紒顔芥崌瀵鈽夐姀鈺傛櫇闂佹寧绻傚Λ娑⑺囬妷鈺傗拺婵懓娲ら埀顒侇殜瀹曟垿骞橀懜闈涘簥濠电娀娼ч鍡浰夐崼鐔虹闁瑰瓨绻傞懜褰掓煕閹垮啫寮慨濠冩そ閺屽懘鎮欓懠璺侯伃闂佸憡蓱閹倿寮婚敐澶婄闁绘劕妯婂ú顓㈡⒑閻熸壆鐣柛銊ョ秺閸╃偤骞嬮悩顐壕闁挎繂绨肩花浠嬫煕婵犲嫬浠辨慨濠冩そ閹虫牠鍩為敐鍛Ш闁诡喗锚椤繈顢栭懞銉р偓娲⒑閻熸澘鈷旂紒顕呭灦閸╂盯骞掗幊銊ョ秺閺佹劙宕ㄩ鍏兼畼闂備礁鎽滈崰鎾诲磻閻愬灚宕叉繛鎴炵鐎氭氨鎲歌箛娑欏仼闁汇垻顣介崑鎾舵喆閸曨剛顦ㄧ紓渚囧枛閻倿宕洪妷锕€绶為柟閭﹀墻濞煎﹪姊洪幎鑺ユ殰闁稿鎹囬弻鐔虹矙閸喗娈诲┑顔硷攻濡炶棄鐣烽妸锔剧瘈闁告劦鐓堝Σ閬嶆⒒娴ｅ懙鍦崲閹寸姷鐭欓柟鎹愵嚙缁犳煡鏌曡箛瀣偓鏇㈢嵁閵忥紕绠鹃柟瀵稿仧閹冲懘鏌涘鍡曢偗婵﹥妞藉畷婊堝箵閹哄秶鍑圭紓鍌欐祰椤曆囧疮閺夋垹鏆︾€规洖娲﹂崰鍡涙煕閺囨娅冪紒銊ヮ煼濡懘顢曢姀鈥愁槱闂佽鎮傜粻鏍嵁濡ゅ懏鍋愰柣顐墮闁帮絽鐣烽幆閭︽闂傚⿴鍓﹂崜姘跺Φ閸曨垰顫呴柍鈺佸暟椤︽澘顪冮妶鍐ㄧ仾妞ゃ劌妫濋獮蹇涘川閺夋垹顦梻濠庡亽閸樼偓寰勯敓锟�
闂傚倸鍊搁崐鎼佸磹閹间礁纾归柟闂寸绾惧湱鈧懓瀚崳纾嬨亹閹烘垹鍊炲銈嗗笒椤︿即寮查鍫熷仭婵犲﹤鍟扮粻缁橆殽閻愭潙鐏村┑顔瑰亾闂侀潧鐗嗛幊鎰版偪閳ь剚淇婇悙顏勨偓鏍涙担鑲濇盯宕熼浣稿妳婵犵數濮村ú锕傚煕閹寸姵鍠愰柣妤€鐗嗙粭鎺懨瑰⿰鈧崡鎶藉蓟濞戙垺鍋愰柛鎰级鐠囩偤鎮楃憴鍕闁搞劌娼￠悰顔碱潨閳ь剟鐛崶銊﹀闁荤喐婢橀崢鐐测攽閿涘嫬浜奸柛濠冪墵瀹曟繈骞嬮敃鈧崹鍌炴煕閿旇骞橀柣顓炵墛閵囧嫰寮村Δ鈧禍鎯р攽椤旂》鏀绘俊鐐舵铻為柛鎰╁妷濡插牊绻涢崱妯曟垿藟閿濆鈷掑ù锝呮嚈瑜版帗鏅濋柕鍫濐槹閸婅埖绻濋棃娑卞剱闁稿鏅犲娲垂椤曞懎鍓抽梻鍌氬鐎氼喚妲愰幒鏂哄亾閿濆簼绨藉ù鐘灮閳ь剝顫夐幐绋课涘┑鍡╂綎闁惧繐婀辩壕鍏间繆椤栨碍鎯堟い顐㈢Т椤啴濡堕崱妯锋嫻闂佺粯顨嗗ú鏍х暤閸曨偀鏀介柣鎰级閳绘洖霉濠婂嫮绠為柟顕嗙節閹垽宕楅懖鈺佸箺闂備礁鎼崐鍦偓绗涘洤绠熼柟闂寸劍閻撶喐銇勯幘璺轰哗閻庢氨澧楅妵鍕敇閳ュ啿濮峰銈忕畳濞呮洟濡甸崟顖毼╅柕澹啠鍙洪柣搴㈩問閸ｎ噣宕戞繝鍥モ偓浣割潩鐠鸿櫣鍔﹀銈嗗笒鐎氼喖鐣垫笟鈧弻鐔兼倻濮楀棙鐣剁紓渚囧亜缁夊綊寮诲鍫闂佸憡鎸鹃崰搴敋閿濆绀冩繛鏉戭儏閻楁岸姊洪崜鎻掍簽闁哥姵鎹囧畷銏ゆ偨閸涘ň鎷洪柣鐘叉礌閳ь剙纾禒顓炩攽閻橆喖鐏弸顏呫亜閿濆懏鍋ユ慨濠勭帛閹峰懘鎼归悷鎵偧闂備浇顫夐幃鍌滅不閺嵮呮殾濞村吋娼欑粻娑㈡煛婢跺寒鍤﹂柨鏇炲€归悡鏇㈡煛閸ャ儱濡奸柣蹇涗憾閺屸剝鎷呯粙鎸庢闂侀潧娲ょ€氫即鐛崶顒€鐓涘ù锝堟〃閹絿绱撻崒娆掑厡濠殿喗鍎抽悾鐑芥偨閸偒娼熼梺瑙勫劤閻°劍鍒婇幘顔界厽闁靛牆楠搁悘鐘绘煕濮楀牏绡€婵﹨娅ｇ划娆戞崉閵娧屽敼闂備焦瀵уú蹇涘垂瑜版帩鏁嬮柨婵嗘缁♀偓濠殿喗锕╅崢钘夆枍濠婂嫮绡€闁靛骏绲介悡鎰版嫅闁秵鐓涢柛婊冨暟缁夘喗鎱ㄦ繝鍛仩缂佽鲸甯掕灒闁告繂瀚峰ḿ鏃傜磽閸屾瑦顦烽柣鎺炵畵楠炴劙骞庨悾灞界ウ闂佸湱澧楀妯肩矆閸愨斂浜滈柡鍐ㄦ肠閹烘绠繛宸簼閳锋垿鏌ゆ慨鎰偓鏇㈠几閹寸偟绡€闁靛繆鍩楅鍕カ缂傚倸鍊烽悞锕佸綘婵炲瓨绮嶇划鎾诲蓟閻旇 鍋撳☉娆嬬細缂佺姰鍎叉穱濠囶敍濡も偓娴滈箖姊婚崒娆掑厡缂侇噮鍨辩粭鐔肺旈崨顓㈡７闂佹寧绻傞ˇ鍗炵暤娓氣偓閹鏁愭惔鈩冪亶闂佸搫鎳忕换鍫ュ蓟瀹ュ牜妾ㄩ梺鍛婃尰缁嬫捇宕氶幒鏃€瀚氭繛鏉戭儐椤秹姊洪棃娑氱畾婵＄嫏鍥х濠电姵纰嶉埛鎴︽煕閹炬潙绲诲ù婊呭仱閺屾盯鎮╅搹顐㈢３闂佺硶鏅涢敃顏勵嚕閹绢喖顫呴柨娑樺楠炲牆鈹戦悩鍨毄濠殿喗鎸冲畷鎰板锤濡も偓閻鏌涢弴銊ュ闁告瑥绻愰埞鎴︽偐閹绘帩浼€闁汇埄鍨遍惄顖炲蓟閻旈鏆嬮柣妤€鐗嗗▓妤呮⒑閸︻厼甯剁紓宥咃躬閹即顢欓懞銉ュ妳闂佽鍎抽崢鏍ㄧ珶閺囩喓绡€闁汇垽娼у瓭濠电偠顕滅粻鎾诲箖閳ユ枼妲堥柕蹇ョ磿閸樺崬鈹戦悙鏉戠仴鐎规洦鍓熷鎼佸Χ閸モ晝锛滈梺缁橈耿濞佳勭闁秵鐓涢悘鐐靛亾缁€瀣偓瑙勬礋娴滆泛顕ｉ幘顔藉亹闁圭粯甯╅悗瀵哥磽閸屾艾鈧兘鎳楅崜浣稿灊妞ゆ牗绮嶅畷鏌ユ煕椤愶絿绠橀柡鍡畵閺屾盯顢曢敐鍡欘槰闂佹悶鍊曢澶愬蓟濞戔懇鈧箓骞嬪┑鍛嚬闂備胶绮换鎰不閹炬剚娼栧┑鐘宠壘绾惧吋绻涢崱妯虹劸婵″樊鍣ｅ铏规喆閸曨厹鍋為梺閫炲苯澧茬紒澶樺枛鐓ゆい蹇撴噺濞呭洭姊虹粙鎸庢拱闁煎綊绠栧畷鎴濐吋婢跺鎷烘繛鏉戝悑閻熝囧礆閺夋鐔嗛悹铏瑰劋閸犳ḿ鈧娲橀崹鍧楃嵁濮椻偓楠炲洦鎷呴悷鏉垮帪濠碉紕鍋戦崐鏍箰妤ｅ啫纾绘繛鎴欏灩缁犳椽鏌ｉ姀鐘冲暈闁抽攱鍨块弻娑樷攽閸℃浠惧┑鐘亾濞寸厧鐡ㄩ悡鐔兼煃閸濆嫸宸ラ柣蹇ョ畵閺岋絽鈽夐崡鐐寸亪闁句紮绲介妴鎺戭潩閻撳海浠柣搴ㄦ涧閻倿寮婚敐澶嬪亹闁告瑥顦遍埞娑㈡倵濞堝灝鏋熼柟姝屽吹缁晠鎮㈤悡搴″祮闂侀潧绻嗗褔骞忕紒妯肩閺夊牆澧介崚浼存煙鐠囇呯瘈妤犵偛妫濆畷濂稿Ψ閿旀儳骞楁俊鐐€栭幐楣冨磿閹邦儵鐔煎焵椤掆偓铻栭柣姗€娼ф禒婊呯磼缂佹﹫鑰跨€殿噮鍋婇獮妯肩磼濡粯顏熼梻浣芥硶閸ｏ箓骞忛敓锟�
闂傚倸鍊搁崐鎼佸磹閹间礁纾归柟闂寸绾惧綊鏌熼梻瀵割槮缁惧墽鎳撻—鍐偓锝庝簼閹癸綁鏌ｉ鐐搭棞闂囧鏌ㄥ┑鍡欏妞ゅ繒濮风槐鎺楀焵椤掍胶绡€闁稿本顨嗛弬鈧梻浣虹帛钃辩憸鏉垮暣閸┾偓妞ゆ巻鍋撴い鏇ㄥ幘濡叉劙骞橀幇浣瑰兊闁哄鐗勯崝宀勫几閹达附鈷戦柛婵嗗閺嗘瑩鏌ｅΔ鈧€氫即宕洪埀顒併亜閹达絾纭剁紒鎰⒒閳ь剚顔栭崰鏇犲垝濞嗘挶鈧礁顫滈埀顒勫箖濞嗘挻鍤戦柛銊︾☉娴滈箖鏌涢…鎴濇灀闁衡偓娴犲鐓ユ繛鎴灻鈺伱归悩娆忔噽绾惧吋銇勯弴鐐村櫣闁诲骏濡囬埀顒侇問閸ｎ噣宕戞繝鍥х畺闁冲搫鍟扮壕鍏间繆椤栫偞鏁遍悗姘偢濮婂宕掑▎鎴ｇ獥闂佺ǹ顑呭Λ婵嗙暦閹存績妲堥柕蹇娾偓铏吅婵＄偑鍊栭悧妤冪矙閹烘垟鏋嶉柣妯煎仺娴滄粓鏌￠崒娑卞劌婵炶偐鍠庨湁婵犲﹤瀚惌瀣煏閸パ冾伃妤犵偞岣块幑鍕姜閻楀牆濯伴梻鍌欒兌鏋い鎴濆暣瀹曟洟骞庨挊澶屽姦濡炪倖甯掗崰姘缚閹邦厾绠鹃柛娆忣槺閻帗顨ラ悙璇ц含妤犵偞岣块幏鐘绘嚑椤掆偓瀵劌鈹戦悩顔肩伇婵炲绋栨晶婵嬫⒑閸濆嫷鍎忛梺甯秮瀵鎮㈤崗鑲╁姺闂佹寧娲嶉崑鎾绘煛鐎ｎ偆銆掔紒杈ㄥ浮楠炴捇骞掗幘鍏呮樊婵犳鍠栭敃銈夆€﹀畡鎵殾闁圭儤鍨熼弸搴ㄦ煙鐎涙ḿ绠撴い顒€顦靛缁樻媴缁涘娈愰梺鍝ュУ閻楃娀骞冮妷鈺傚亗閹艰揪绲惧▓楣冩⒑閸︻厼顣兼繝銏★耿瀹曪繝骞庨懞銉у幗闂婎偄娲﹂崙褰掑吹濞嗘垹纾界€广儱鎷戦煬顒侇殽閻愭彃鏆欐顏冨嵆瀹曞ジ鎮㈡搴㈩€嶆繝鐢靛О閸ㄧ厧鈻斿☉銏″剹闁割偁鍎遍懜褰掓煟閵忕姵鍟為柍閿嬪灴閹綊宕堕妸銉хシ闂佹悶鍊涙禍顒傛閹炬剚鍚嬮柛娑卞櫘濡箓鎮楃憴鍕；闁告鍟块锝嗙鐎ｅ灚鏅濋梺闈涚墕鐎氼噣鎮峰┑瀣拻濞达絽鎲￠幆鍫ユ偠濮樼厧浜扮€规洘娲熷濠氬Ψ閿曗偓娴滄鈹戦悙鍙夘棞缂佸墎鏌夐妵鎰板箳閹惧厖绨甸梺纭呭閹活亞寰婃ィ鍐ㄧ疅闁绘挸绨堕弨浠嬫煟閹邦厽缍戞慨锝呮閺屾盯濡烽敐鍛瀷闂佸憡锕㈠ḿ褔鈥旈崘顔嘉ч柛鈩冿供濮婂潡鎮楃憴鍕闁轰礁鎽滈崚鎺楁晲婢跺﹦鐫勯梺閫炲苯澧存鐐茬墦婵℃悂鏁傞崜褏妲囬梻浣告啞娓氭宕抽鐣岊浄闁冲搫鎳忛埛鎴︽煕濞戞﹫鍔熷褜鍓熼弻锝呂旈崘銊愩垺銇勯弴顏嗙М妤犵偞锕㈤、娆撴寠婢跺鐩庨梻鍌欑閹诧紕缂撻崸妤€纾块弶鍫氭櫅缁躲倝鏌涢…鎴濇灀闁衡偓娴犲鐓ユ繛鎴灻鈺伱瑰⿰鍐﹀仮闁哄本绋掔换婵嬪礃閵娧傜礉闁诲氦顫夊ú婊堛€佹繝鍥﹂柟鐗堟緲缁犳娊鏌熼幆褏鎽犻柣婵囩墬娣囧﹪鎮欓鍕ㄥ亾閺囩姵宕查柟鎵閸嬪鏌涢弴銊ョ仩闁绘帒鐏氶妵鍕箣閿濆棛銆婂銈忚缁犳捇寮诲鍥ㄥ珰闁哄被鍎卞鏉课旈悩闈涗沪闁挎岸鏌ｉ敐鍥у幋鐎规洖鐖奸幊婊堝极鐏炵喎鍟犻弨浠嬫煥濞戞ê顏╁ù婊冦偢閺屾稒绻濋崘顏勨拰濡ょ姷鍋為崝鏍Χ閿濆绀冮柕濞у懎鐐婇梻浣烘嚀閸氬鎮鹃鍫濈鐎广儱顦壕濠氭煟閺冨浂鍟忕憸鐗堝笚閸嬪倿骞栨潏鍓хɑ闁规彃銈稿娲箮閼恒儲鏆犻梺鎼炲妼濞尖€愁嚕鐠囨祴妲堟俊顖炴敱椤秴鈹戦绛嬫當闁绘锕顐ｃ偅閸愨晝鍘介柟鑹版彧缁辨洘绂掑☉銏＄厽闁绘柨寮跺▍濠勨偓娈垮枦椤曆囶敇婵傜ǹ閱囨い鎰剁秵閳ь剙娲缁樻媴閸涘﹤鏆堥梺瑙勬倐缁犳牕鐣烽悧鍫熷劅妞ゎ厽鍨堕弲顏堟⒑閹稿海绠撴俊顐ｇ〒瀵囧焵椤掆偓閳规垿顢欓弬銈勭返闂佸憡枪濡嫰鍩㈠澶婎潊闁靛牆妫岄幏娲煟閻樺厖鑸柛鏂胯嫰閳诲秹骞囬悧鍫㈠幍闂佸憡鍨崐鏍偓姘炬嫹
婵犵數濮烽弫鍛婃叏閻戣棄鏋侀柛娑橈攻閸欏繘鏌ｉ幋锝嗩棄闁哄绶氶弻娑樷槈濮楀牊鏁鹃梺鍛婄懃缁绘劙婀侀梺绋跨箰閸氬绱為幋锔界厱闁靛ǹ鍎遍埀顒€顭烽獮澶愬箹娴ｇ懓浜遍梺鍓插亝缁诲嫰鎮烽弻銉︹拺缂佸灏呭銉╂煟閺嵮佸仮鐎殿喛顕ч埥澶愬閳哄倹娅囬梻浣虹帛钃辩憸鏉垮暞閹便劍鎯旈妸锔规嫼濠殿喚鎳撳ú銈夊焵椤掍緡娈滅€规洘鍨块獮姗€鎳滈棃娑樼哎婵犵數濞€濞佳囶敄閸℃蛋澶愬醇閻旇櫣顔曢梺鐟扮摠缁诲倿鎳滆ぐ鎺撶厱闁圭偓褰冨畵鍡樻叏婵犲啯銇濈€规洏鍔嶇换婵嬪川椤撗勵棨缂傚倸鍊搁崐鍝ョ矓閹绢喗鏅濇い蹇撶墛閸嬫ɑ銇勯弴妤€浜鹃悗娈垮枙缁瑦淇婇幖浣规櫆闁告搩鐏濋妶澶嬧拻濞达絽鎲￠崯鐐烘煙缁嬫寧顥㈢€规洏鍎甸弻銊р偓锝庝簽娴犲摜绱撴担铏瑰笡缂佽鍊块崺銏ゅ箻鐠囨彃鐎銈嗘煥瑜扮偤宕Δ鍛拻濞撴埃鍋撴繛浣冲洦鍋嬪┑鐘叉搐缁犳牠鏌涚仦鎯у毈闁搞倖娲栭埞鎴︽偐瀹曞浂鏆￠梺绋款儏鐎氫即寮婚敐澶婄闁诲繑妞挎禍顏勵嚕閹间礁纾奸柣鎰ˉ閹锋椽姊洪崨濠勨槈闁挎洏鍎插鍕礋椤栨稓鍘遍柣搴秵娴滄粓顢旈浣典簻闁靛牆鎳庨埀顒€鐏濋～蹇旂節濮橆剛锛滃┑鐐叉閸╁牆危椤曗偓濮婅櫣娑甸崪浣告疂缂備胶绮换鍌炴偩瀹勬噴娲敂閸曨収妲版俊鐐€栧Λ渚€宕戦幇鐗堟櫖婵炴垯鍨洪埛鎴︽煟閻斿憡绶查柍閿嬫⒒缁辨帡顢氶崨顓犱桓闂佽鍣换婵嬪箖閵忋倖鍋傞幖杈剧秵閸熷洦绻濋悽闈涘壋缂傚秴妫濆畷婊冣枎閹惧磭鍔﹀銈嗗灦閸庢娊鍩€椤掍焦绀€闁绘粌顭峰畷绋课旈埀顒傜不濞戙垺鐓熸俊銈傚亾闁绘绻樺畷銏ゆ濞戣鲸瀵岄梺闈涚墕濡瑩藟閸℃稒鐓曢悗锝庡亜婵秶鈧娲樺浠嬪极閹版澘鐐婇柨婵嗘噸婢规洟鏌ｉ悢鍝ユ噧閻庢凹鍘剧划鍫ュ礃閳哄啰顔曢梺鑲┾拡閸撴瑩寮稿☉銏＄厽婵炴垵宕弸鐔兼煙椤栨稒顥堝┑鈩冩倐閺佸啴鍩€椤掑嫭鍎岄柛鏇ㄥ墰缁♀偓闂侀潧楠忕徊鍓ф兜妤ｅ啯鐓犳繛鑼额嚙閻忥箓鏌ｅ☉鍗炴珝妤犵偞甯掕灃濞达絽寮剁€氳棄鈹戦悙鑸靛涧缂佸弶瀵ч悘娆撴⒑鐠団€虫灍闁搞劌婀卞Σ鎰板箳閹炬潙顎撻柣鐔哥懃鐎氼剟宕径鎰€垫繛鍫濈仢閺嬬喓鎲搁弶鍨殻闁靛牜浜濈€靛ジ寮堕幋锕€鏁规繝鐢靛█濞佳兠洪埡鍐╊偨闁靛骏绱曠弧鈧梺姹囧灲濞佳冪摥闂備焦瀵уú蹇涘磹濠靛绠栫憸搴ｆ崲濠靛鐐婇柕濞垮劙缁ㄧ敻姊绘担鍛婃儓婵炲眰鍔戝畷浼村幢濡⒈娲稿┑鐘诧工閻楀﹪鎮″▎鎾寸厸濠㈣泛锕︽禒銏°亜閿濆棗鈻曢柡宀€鍠栭、娆撳垂椤旂粯鐫忕紓鍌欐祰妞村摜鏁敓鐘茬畺闁冲搫鍟版す宕囩棯椤撶偞鍣抽柛瀣崌瀹曠ǹ螖娴ｅ搫骞愰梺璇茬箳閸嬫稒鏅舵禒瀣叀濠㈣泛顑冩禍婊勩亜閹板墎鎮肩紒鐘靛仦閵囧嫰濮€閳藉懓鈧潡鏌熼瑙勬珚鐎规洘锕㈠畷锝嗗緞鐏炰粙鍙￠梻鍌氬€搁崐鎼佸磹瀹勬噴褰掑炊椤掑鏅梺鍝勭▉閸樿偐绮ｅΔ浣虹闁规惌鍘界欢娑氱磽瀹ュ棛澧い顓℃硶閹瑰嫰鎼归崷顓濈礃缂傚倷鑳舵慨闈浳涢崘顔艰摕闁挎繂顦猾宥夋煕鐏炴崘澹樺ù鐘筹耿濮婅櫣绱掑Ο鍝勵潓闂佹寧娲╃粻鎾荤嵁婢跺瞼鐭欐繛鍡樺劤閹垿姊洪幖鐐插姉闁哄懏鐟х划顓熷緞閹邦厸鎷洪梺鐓庮潟閸婃洟寮稿☉銏＄厱閻庯綆浜峰銉╂煏閸℃ê绗氱紒缁樼箓椤繈顢橀悩鎻掑闂傚倷绀佹竟濠囧磻閸涱垱宕查柛宀€鍋涘Ч鍙夌箾閸℃绠氶柡鈧禒瀣叆婵炴垶锚椤忣亝绻涢崨顔界缂佽鲸甯楀ḿ蹇涘Ω閵夛箒鐧佹俊鐐€戦崹娲偡閿斿墽绱﹂柣锝呯灱閻瑩鏌涢…鎴濇灈鐎殿喖鍢查埞鎴炲箠闁稿﹥顨嗛幈銊╂倻閽樺锛涘┑鐐村灍閹崇偤宕堕澶嬫櫖濠电娀娼ч悧鍛姳閻戣姤鈷掗柛灞剧懅椤︼箓鏌熷ù瀣⒉缂佹鍠庤灃闁告侗鍘鹃悰銉モ攽鎺抽崐鎰板磻閹剧粯鐓冮悹鍥皺鏁堟繝娈垮枓閸嬫捇姊洪棃娑氬婵☆偄鐭傞獮蹇撁洪鍛幗闂佺粯锚閸樻牠鎳滈鍫熺厱闁哄倽鍎荤€氫即鏌嶇拠鑼ф鐐叉喘閹囧醇閵忕姴绠ラ梻鍌欑閹诧繝宕归鐐茬９闁哄稁鍋€閸嬫挸顫濋悙顒€顏�