专用短波接收机射频前端预选滤波器的设计与实现

为了得到性能较好的射频接收机前端，滤除接收机中的各种干扰信号，保留有用信号，必须在接收机前端适合的地方放置滤波器。尤其是放置于系统第一级的预选滤波器，它的性能好坏直接影响了整个接收机射频前端的噪声系数。通过分析N 级级联系统噪声系数方程可知，必须将预选滤波器的损耗降到最低，同时还必须使其具有系统需要的选择性。

1、预选滤波器的选择

由于预选滤波器处于整个射频前端系统的第一级，其性能对整个接收机系统产生极大的影响，考虑到系统的线性度（避免非线性误差带来噪声），预选滤波器中不应有任何有源器件，因此该滤波器应设计为无源LC滤波器^[1]。

同时，对于专用短波接收机系统来说线性的相位响应（相移）要比陡峭的衰减或幅度变化更为关键，而且线性的相移和陡峭的幅度变化是相互冲突的。综合考虑其相互影响并结合系统要求，文中设计选择了衰减曲线中波纹最小的最大平滑巴特沃兹（Butterworth）带通滤波器。

2、预选滤波器的设计与实现

2.1、预选滤波器的设计方法

目前，模拟带通滤波器的设计方法都是将要设计的滤波器的技术指标通过某种频率转变关系转换成模拟低通滤波器的技术指标，并依据这些技术指标设计出低通滤波器的转移函数，然后再依据频率转换关系变成所要设计的滤波器的转移函数^[2]。

模拟带通滤波器的4个频率参数是Ω_sl、Ω₁、Ω₃、Ω_sh，其中Ω₁、Ω₃ 分别是带通的下限与上限频率，Ω_sl是下阻带的上限频率，Ω_sh是上阻带的下限频率，首先要将它们做归一化处理。

定义Ω_BW =Ω₃ -Ω₁ 为带通的带宽，并以此为参考频率对Ω轴做归一化处理，即
η_sl =Ω_sl /Ω_BW，η_sl =Ω_sh /Ω_BW，
η₁ =Ω1 /Ω_BW，η₃ =Ω₃ /Ω_BW。

再定义Ω=Ω₁Ω₃ 为带通的中心频率，归一化的η=η₁η₃，从而可以得出其归一化的幅频特性H（jη）及归一化的低通幅频特性| G（jλ）|，进而可以得出η和λ的一些主要对应关系。在η₂ - η₃ 之间找一点η，它在λ轴上对应的点应在0 - λ_P 之间，由于η₃ =η /η₁，那么η在η轴上对应的点应是η/η，而λ在λ轴上对应的点应是-λ。这样又可找到η与λ的转换关系为

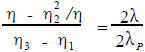（1）

由于η₃ -η₁ = 1，λ_P = 1，所以有

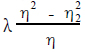（2）

从而实现了频率转换。利用所得到的低通滤波器技术指标λ_P、λ_s、α_P、α_s，可设计出滤波器的转移函数G（p）。由

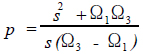（3）

可得

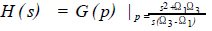（4）

这样，所需的带通滤波器的传递函数可以求出。

通过上述方法可以将巴特沃兹模拟带通滤波器的设计转化成巴特沃兹模拟低通滤波器的设计^[3]。注意，N 阶的低通滤波器转换到带通后，阶次变为2N。

给定模拟低通滤波器的技术指标α_p、Ω_p、α_s、Ω_s，其中αp 为通带内允许的最大衰减，α_s 为阻带内应达到的最小衰减，α_p、α_s的单位为dB，Ω_p 为通带上限角频率，Ω_s 为阻带下限角频率^[4]。

α_p、α_s 都是Ω的函数，它们的大小取决于|G（jΩ）|的形状，为此，定义一个衰减函数α（Ω），即

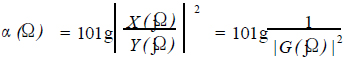（5）

这样，式（5）把低通模拟滤波器的4个技术指标和滤波器的幅平方特性联系了起来。

由于每一个滤波器的频率范围存在很大差别。为了使设计规范化，需要将滤波器的频率参数作归一化处理。设所给定的实际频率为Ω（或f），归一化后的频率为λ，对低通滤波器，令

λ =Ω /Ω_p（6）

令归一化复数变量为p，p = jλ，显然

p = jλ = jΩ /Ω_p = s /Ω_p（7）

巴特沃兹低通模拟滤波器的设计可以按以下3个步骤来进行。

1）将实际频率Ω归一化

得归一化幅平方特性

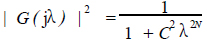（8）

由此可以看出|G（jλ）|²（或|G（jΩ |²）中只有2个参数C和N，N 是滤波器的阶次。

2）求C和N

由（5）式得

α（λ）= 101g（1 + C²λ^2N），（9）

则公式，

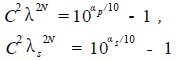（10）

因为λ_p = 1，所以

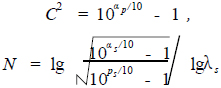（11）

这样C和N 可求。

若令α_p = 3 dB，则C = 1，这样巴特沃兹低通模拟滤波器的设计就只剩下一个参数N。

3）确定G（s）

因为p = jλ，有

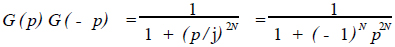（12）

由1 +（-1）^Np^2N = 0

解得

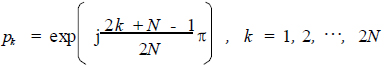（13）
 
这样，G（p）G（- p）的2N 个极点等分在s平面半径为一的圆上，相距为（π/N）rad。
 
为了保证所设计的滤波器是稳定的，应把左平面的极点赋予G（p），即
 
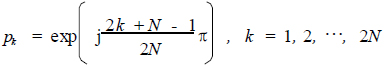（14）

这样

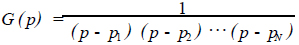（15）

若N 为偶数，G（p）的极点皆是共轭出现，即

p_k，p_{N +1 - k}，1 ≤ k ≤N /2 （16）

这一对共轭极点构成一个二阶系统，即

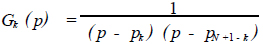（17）

总的转移函数应是N /2类型的二阶系统的级联，即

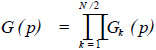，N 为偶数。（18）

若N 为奇数，它将由一个系统和（N - 1）/2个二阶系统相级联，即

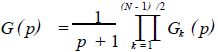，N 为奇数。（19）

这样，就得到了归一化的转移函数G（p）。利用式（7）关系，即得实际需要的G（s）。

为实现二端口梯形的转移函数G（s），重点在于利用G（s）求出z₁₁和z₂₂，然后实现z₁₁和z₂₂。转移函数的零点与z₂₁的零点相一致，所以不必求z₂₁。

推导z₂₁和z₂₂的基本思想是输入LC网络的平均功率应等于LC网络输出的平均功率。为此，定义辅助有理函数K（s）和K（ω²）使

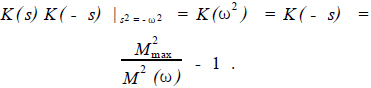（20）

式中：M（ω）= |H（jω）|是幅频响应，且Mm ax（ω）=是幅频响应的最大值。K（ω²）是ω的偶有理函数，K（- s²）是具有实系数的关于s的偶有理函数，且

K（ω²）≥ 0（21）

K（- s²）的复零点以象限对称的形式出现，即，s₁ =σ₁ + jω₁，s₂ =σ₁ - jω₁，s₃ = 2σ₁ + jω₁，s₄ = -σ₁ -jω₁，σ₁ 和ω₁ 是正实数。由于K（s）是具有实系数的有理函数，所以必须从s复平面的左半平面或右半平面选择复共轭零点对。

K（- s²）的实零点成对出现，即s₁=σ₁，s₂ = -σ₁。对K（s）只选择一个零点即可。

用于求二端口梯形实现的归H_n（s）为

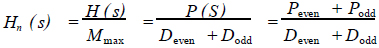（22）

式中：D_even是关于s的偶多项式，D_odd是关于s的奇多项式。P（s）由转移函数的零点决定，P_even是关于s的偶多项式，P_odd是关于s的奇多项式。

由式（22）可求出

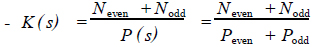（23）

式中：N_even是关于s的偶多项式，N_odd是关于s的奇多项式。采用K（s）的极点作为转移函数的零点。

可以看出

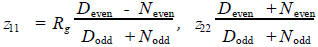
阻抗z₁₁可以由经典的福斯特法实现。

根据上述方法可实现系统所需求的巴特沃兹带通模拟滤波器。利用ADS对所设计的系统进行仿真，如图1所示。

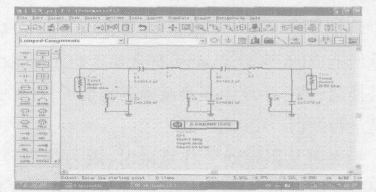
图1、利用ADS仿真LC滤波器

仿真结果如图2所示。

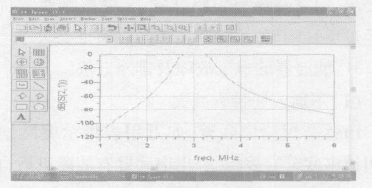
图2、LC滤波器频率响应仿真结果

2.2、预选滤波器的实现

2.2.1、电感元件的制作

通过以上分析可以设计出符合要求的LC滤波器，但是滤波器的实现却存在一定的难度。实现滤波器，主要是实现高精度、高Q 值、高自谐振频率以及寄生参量较小的电感。一般来说，对于电感值较小的电感，采用漆包线直接绕制空心线圈而成^[5]。

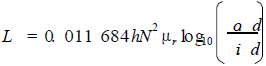（24）

式中：L 为电感值；h为磁环厚度；o d为磁环外径；I d为磁环内径；μ_r 为磁环磁感系数；N 为线圈轧数。

绕制成型后选择一50 pF左右的电容与其串联，根据LC振荡电路原理，利用矢量网络分析仪测出其并联谐振点。通过LC与谐振频率的换算关系，就可以得出L 的准确值。

2.2.2、预选滤波器的调整

滤波器装配完成以后，就要测量各项电特性。如果某些性能不能满足技术要求，就要进行调整，直到达到技术要求为止。

调整过程如下：

1）在印制板上进行调谐，谐振回路和其他元件断开，引线应尽量短，以使调谐准确。
2）调谐完成以后，把各点连接起来便构成滤波器。首先测量通带的反射衰减。如果调谐好的谐振频率已发生较大的偏移，要重新检查并调整谐振频率。如果反射衰减仅在个别点上稍低于要求值，可以微调衰减峰频率使之符合要求。 
3）如果通带衰减太大，一个原因是原件的Q 值太低所造成的。这时候，把不符合要求的元件找出来并替换之；另一个原因是衰减峰频率偏了，这时候要重新进行调谐。 
4）在测量阻带的工作衰减时，因为频率较高，如果遇到阻带要求高的滤波器，有时个别点会不符合要求。这时可微调衰减峰频率，使整个阻带特性符合要求。但衰减峰频率调过后，又会影响通带特性。需经过反复调整，才能使二者同时满足要求。

2.2.3、滤波器的常见故障及排除方法

（1）不通或通带衰减大

1）逐节短路串联臂。如万用表指示突然增大，表明该串联臂有故障。查出串联臂有故障以后，再按照上述方法检查该节哪些元件发生故障。 
2）如果串联臂经过检查后没有故障，就再检查并联臂。检查时要逐个断开并联臂，查出某节并联臂有故障后，再用同样的方法检查该节元件有无故障。 
3）通带中高频端衰减增大，可测上阻带的衰减峰频率和谐振衰减。低频端衰减增大，可测下阻带的衰减峰频率和谐振衰减。

（2）通带内衰减波动大

1）分别检查串联臂和并联臂的谐振频率。
2）检查电容器的绝缘电阻。
3）重新调谐或更换元件。

（3）阻带衰减下降

1）并联臂元件Q 值下降。测量电感、电容的Q值。
2）并联臂谐振频率有偏移。测量谐振频率。
3）接地端子接触不良。用万用表检查。

（4）非线性失真增大

1）磁芯受震移位，改变了磁路的气隙，造成磁饱和，使谐波增大。可用高、低电平分别测量电路的谐振频率，若谐振频率随电平高低而变，表明磁芯有磁饱和现象，应予更换。
2）电容元件接触不良，虚焊等形成活动性电阻，引起谐波增大。可用阻抗电桥测试电容器的接触电阻，用万用表检查原件接头的接触电阻。

（5）平衡滤波器的平衡衰减下降

1）串联臂元件变值或对地绝缘不良，造成上下不对称。应逐节测量平衡衰减以确定故障所在。
2）并联臂有对地短路现象。应检查并联臂元件对地绝缘程度。

（6）阻抗特性不好（反射衰减太小）

1）分别检查串联臂和并联臂的谐振频率。
2）检查元件值有无变化。

3、结束语

总之，专用短波接收机在设计和实现上越来越趋向高性能、高集成度方向发展。在性能上，接收机主要是向高线性、大动态范围、高灵敏度、高分辨率等方面发展。而要实现这些目标最重要的是实现接收机性能优良的滤波器。文中正是根据这样的需求，从理论算法的角度分析并实现了一种满足专用短波接收机射频前端系统指标要求的预选滤波器。

作者：陈国宇，韦金辰

参考文献：

[1]刘长军，黄卡玛，闫丽萍。射频通信电路设计[M]。北京：科学出版社，2005。
[2]胡广书,数字信号处理理伦、算法与实现[M]。第二版。北京：清华大学出版社，2003。
[3]ULR ICH L R DAV ID P.NEWKIRK. RF /Microwave circuit design forwireless[M]。北京：电子工业出版社，2004。
[4]M IROSLAV D，DEJAN V，BR IAN L.Filter design for signal processing using MATLAB and mathematica [M]。北京：电子工业出版社，2004。
[5]JOSEPH J.Secrets of RF circuit design[M]。北京：电子工业出版社，2001。