- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
射频微带滤波器基础理论
频率的提高意味着波长的减小,该结论应用于射频电路中,就是当波长与分立元件的集合尺寸相比拟时,电压和电流不再保持空间不变,以波的形式进行传播。经典的基尔霍夫电压和电流定律没有考虑电压和电流在空间的变化,则必须对普通的集总电路做重大的修改。
本章首先介绍了射频微带滤波器设计中所涉及的基本概念,然后介绍了二端口网络理论和谐振与耦合理论。
1、传输线理论
1.1、均匀传输线的概念和模型
频率提高后,导线中所流过的高频电流会产生趋肤效应,工程上常用趋肤深度δ来描述这种趋肤效应,δ为电磁波场强的振幅值衰减到表面值1/e所经过的距离,由于趋肤效应使得导线有效面积减小,高频电阻加大,而且沿线各处都存在损耗,这就是分布电阻效应;通高频电流的导线周围存在高频磁场,这就是分布电感效应;由于两导线之间有电压,故两线之间存在高频电场,这就是分布电容效应;由于两线间的介质并非理想介质而存在漏电流,这相当于双线间并联一个电导,这就是分布电导效应。基于上述的物理事实,便可得出双线传输线等效模型如图1所示。
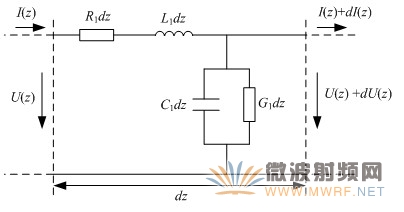
图1 双线传输线等效模型
图1中,R1为单位长度的分布电阻,L1为单位长度的分布电感,G1为单位长度的分布电导,C1为单位长度的分布电容。
1.2、均匀传输线相速与波长
相位速度是等相位面传播的速度,简称相速。在均匀传输线理论中等相位面是垂直于z轴的平面,相速Vp为
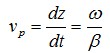 (1)
(1)
在一个周期的时间内波所行进的距离称为波长,波长λp为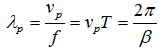 (2)
(2)
其中f为电磁波频率,T为振荡周期。
1.3、均匀传输线特性阻抗
入射电压与入射电流之比或反射电压与反射电流之比称为特性阻抗(即波阻抗),特性阻抗Z0为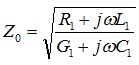 (3)
(3)
对于微波传输线由于频率很高,R1<
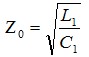 (4)
(4)
1.4、均匀传输线传播常数
传播常数γ表示行波经过单位长度后振幅和相位的变化,其表示式为
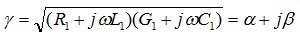 (5)
(5)
由于实际微波传输线的损耗R1、G1比ωL1、ωC1小得多,式(5)经变换后可得
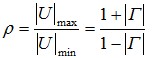 (6)
(6)
其中: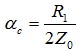 ——由导体电阻引起的损耗;
——由导体电阻引起的损耗;
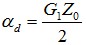 ——由导体间介质引起的损耗。
——由导体间介质引起的损耗。
αc、αd说明传输线上的信号衰减是由导体电阻的热损耗和导体间介质极化损耗共同引起的。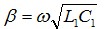 (7)
(7)
一般情况下,传播常数为复数,其实部α为衰减常数,单位为dBm;β为相移常数,单位为rad/m。
1.5、传输线的反射系数与电压驻波比
传输线上某处反射波电压(或电流)与入射波电压(或电流)之比为反射系数,用Γ(z´)表示
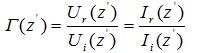 (8)
(8)
考虑到负载阻抗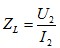 ,故式(8)可写为
,故式(8)可写为
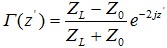 (9)
(9)
在传输线的终端(负载端)z´处,终端反射系数用Γ2表示,由式(9)得
 (10)
(10)
因此,
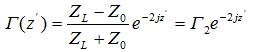 (11)
(11)
由式(11)可见,终端反射系数只与负载阻抗和传输线的特性阻抗有关。
当电磁波在终端负载不等于传输线特性阻抗的传输线上传输时,会产生反射波。反射波的大小除了用电压反射系数来描述外,还可用电压驻波系数VSWR(Voltage Standing Wave Ratio)或行波系数K来表示。驻波系数ρ定义为沿传输线合成电压(或电流)的最大值和最小值之比,即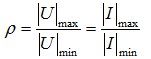 (12)
(12)
传输线上合成电压(或电流)振幅值的不同,是由于各处入射波和反射波的相位不同引起的。当入射波的相位与该点反射波的相位同相时,则该处合成波电压(或电流)出现最大值;反之两者相位相反时,合成波电压(或电流)出现最小值,故有
|U|max=|Ui|+|Ur|=|Ui|(1+|Γ|) (13)
|U|min=|Ui|-|Ur|=|Ui|(1-|Γ|) (14)
可得到驻波系数和反射系数的关系式为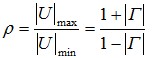 (15)
(15)
或者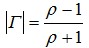 (16)
(16)
因此,传输线的反射波的大小可用反射系数的模、驻波系数和行波系数来表示。反射系数的范围为0≤|Γ|≤1,驻波系数的范围为1≤ρ≤∞。当|Γ2|=0、ρ=1表示传输线上没有反射波,即为匹配状态。
1.6、传输线的工作状态
传输线的工作状态指的是传输线上电压和电流的分布状态,传输线的工作状态取决于终端负载。
(1)当ZL=Z0(即负载匹配)时,终端反射系数Γ2=0,反射波电压和反射波电流均为零,称为行波状态。
(2)当ZL=0(即负载短路)时,终端反射系数Γ2=-1。
(3)当ZL=∞(即负载开路)时,终端反射系数Γ2=1。
在第(2)和(3)种情况下,反射波与入射波幅度相同(负号表示反射波与入射波相位相反),称为全反射状态。
在一般情况下,0<|Γ2|<1,称为部分反射。
1.7、均匀传输线输入阻抗
终端接负载阻抗时,则从距终端为z′处向负载方向看过去的阻抗为输入阻抗,定义为该点的电压U(z')与电流I(z')之比,并用Zin表示。
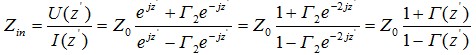 (17)
(17)
1.8、史密斯圆图
史密斯圆图是以保角映射原理为基础的图解方法,通过史密斯圆图,可以让使用者迅速的得出在传输线上任意一点阻抗,电压反射系数,VSWR等数据,简单方便,所以在电磁波研究领域一直被广泛应用。虽然随着各种微波CAD软件的发展,已经很少进行手工计算,但在利用软件对射频电路进行设计和分析时掌握史密斯圆图的意义仍然十分重要。
2、微带传输线理论
微带传输线是50年代发展起来的一种微波传输线。与金属波导相比,它具有体积小、重量轻、使用频带宽、可集成化并能构成各种用途的微波元件等优点,但损耗稍大,Q值较低,功率容量小。微带线一般用薄膜工艺制造,介质基片选用介电常数高、微波损耗低的材料,常用的介质基片材料有氧化铝陶瓷、氧化铍、蓝宝石、铁氧体、聚四氟乙烯等。导体薄膜应具有导电率高、稳定性好、与基片的粘附性强等特点。
2.1、微带传输线的结构
微带传输线一般制作工艺是将基片研磨,抛光和清洗,然后将基片放在真空镀膜机中形成一层铬-金层,再利用光刻技术制作所需的电路,最后采用电镀方法使导体带和接地板达到所要求的厚度(3~5倍趋肤深度),并装上所需要的有源器件和其他元件形成微带电路。因此,微带传输线可以看作是由双导体传输线演变而来的双导体微波传输线,图2所示为微带传输线结构示意图。
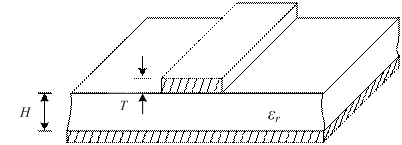
图2 微带线的结构示意图
图2中,εr表示介质基片的有效介电常数,H表示介质基片的厚度,T表示导体薄膜的厚度。微带线为开放式双导体微波传输线,传输的主模是横电磁TEM(Transverse Electric and Magnetic)波。在微带传输线中,导体与接地板之间填充有介质基片,而其余部分为空气,导体周围的填充介质分别由媒质A(基片)和媒质B(空气)两种媒质组成。
任何模式的电磁场除了应满足介质与理想导体的边界条件外,还应满足介质与空气交界面的边界条件。单独的TEM模式不能满足微带线边界条件的要求,因此,在微带传输线中传输的电磁波的模式含有横电TE(Transverse Electric)模和横磁TM(Transverse Magnetic)模。
一般而言,基片的介电常数大于空气的介电常数,因此电场强度E在基片中的分布比较大,而且基片相对于外部空气媒质而言较薄,磁场强度H在基片中的分布也大于在空气媒质中的分布,所以从电磁场的分布角度看,微带传输线中传输的电磁波可以近似认为TEM模,或者说,在微带传输线中传输的电磁波为准TEM模。微带中的能量大部分集中在中心导体下面的介质基片中进行传播。
2.2、微带传输线的特征参数
微带线的特性阻抗和有效介电常数是设计微带谐振器、滤波器、天线等微波无源器件时需要首先确定的参数。
当微带线传输TEM波时,其特性阻抗可表示为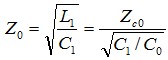 (18)
(18)
其中L1、C1分别为微带线单位长度的分布电感和分布电容,C0是空气全填充时单位长度分布电容。
求解C0和C1的问题是一个静态场的问题,其求解方法较多,常用的有保角变换法,谱域法,有限差分法和积分方程法。
惠勒给出了Z0的近似计算公式:
当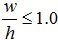 时
时
 (19)
(19)
当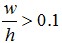 时
时
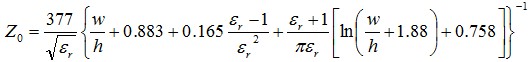 (20)
(20)
哈梅斯泰德给出的近似计算公式具有较高的精确度,并且对宽带和窄带均适应,Pucel也给出了近似计算公式。
2.3、微带传输线的损耗
微带传输线损耗是在设计微波滤波器、双工器、谐振器等微波无源器件时需要特别考虑的问题。
从图2中可以看出,微带传输线是半开放式结构。微带传输线的损耗包括导体损耗、介质损耗、辐射损耗等。微带传输线是半开放式结构,辐射损耗是微带线向外辐射电磁波引起的能量衰减。
除硅和砷化镓等半导体基片外,大多数微带线上的导体损耗远大于介质损耗,在实际应用中,介质损耗一般可以忽略。
谐振器的无载品质因数Qu是一个反映谐振器本身能耗情况以及选频特性的重要参量。一般情况下,谐振器的Qu值越大,该谐振器的能耗越小,其频率选择性也越好。显然,利用MgB2超导薄膜制成的高Qu微带谐振器设计的带通滤波器可以有效降低通带损耗,同时通过增加谐振器的阶数可以提高微带滤波器的选频特性。
2.4、微带谐振器
在本论文中主要用到的是矩形微带谐振器,如图3所示。
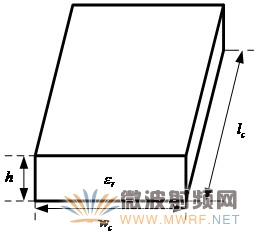
图3 矩形微带谐振器修正模型
图3中lc是矩形谐振器的线长,Wc是矩形谐振器的线宽,h是矩形谐振器的介质层厚度,εr是矩形谐振腔等效相对介电常数。
两端开路的矩形微带线,通过适当的激励可以在导带和接地板之间产生电磁振荡,形成矩形谐振腔。上下导体片看作理想电壁,谐振器四周看成理想磁壁。实际上,有部分电磁能量向外泄漏,腔内电磁场在各个方向上呈驻波分布,谐振器的纵向长度l必定是半波长的整数倍。
滤波器的中心频率以及微带线有效介电常数可以确定谐振器的谐振波长,通常用于制作微带滤波器的传输线长度为λ/2或λ/4,但是由于λ/4传输线需要在超导薄膜和基片上通孔以进行接地,一方面会引入很大的过孔损耗,另一方面在微带线上难以加工,所以在超导滤波器的设计中经常采用λ/2的传输线。
将λ/2谐振器进行各种变形可以减小超导微带滤波器的有效尺寸,几种常见的半波长谐振器结构如图4所示。
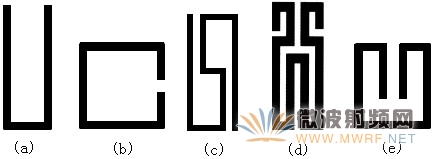
图4 几种常用的半波长谐振器
在图4中,(a)为标准发夹型半波长谐振器,(b)是半波长开环谐振器,(c)、(d)、(e)为发夹型谐振器的几种变形结构,均可用于滤波器的小型化设计。
2.5、超导滤波器制作工艺精度引起的问题
超导滤波器的滤波特性主要由导带宽度w、导带长度l、基片厚度h和介电常数εr等参数决定。超导滤波器制作过程中所涉及到的光刻精度,腐蚀程度,介质基片的一致性都会对滤波器滤波特性产生影响。通常采取灵敏度分析法,估算出给定加工误差条件下微带线传输特性的最坏情况,以此分析器件的性能。
3、二端口网络理论
网络理论是一种非常普遍的处理问题的方法,它把系统用一个由若干端口对外的未知网络表示。微波网络理论是微波工程强有力的工具,主要研究微波网络各端口的物理量之间的关系,实际的微波/射频滤波器也是用网络分析仪进行测量。微波网络分为线性与非线性,有源与无源,有耗与无耗,互易与非互易。
双口元件是在微波工程中应用最多的一种元件,主要有滤波器、移相器、衰减器等。与单口元件相似,双口元件一般采用网络理论进行分析,但是,值得指出的是元件的网络参数本身还是需要用场论方法求得,或者实际测量得到,从这个意义上讲,场论是问题的内部本质,而网络则是问题的外部特性。
几乎所有的微波元件都可以由一个网络来代替,并且可以用网络端口参考面上的变量来描述其特性(在传输线上端口所在的位置,与能流方向垂直的横截面通常称为"参考面")。选择参考面的原则是在该参考面以外的传输线上只传输主模。
微波网络有不同的网络参量:阻抗参量Z、导纳参量Y和A参量反映的是参考面上电压与电流的关系;散射参量S、传输参量T反映的是参考面上归一化入射波电压和归一化反射波电压之间的关系。在微波频率下,阻抗参量Z、导纳参量Y和A参量不能直接测量,所以引入散射参量S和传输参量T。利用S参数,射频电路设计者可以在避开不现实的终端条件以及避免造成待测器件损坏的前提下,用两端口网络的分析方法来确定几乎所有射频器件的特征,故S参量是微波网络中应用最多的一种主要参量。
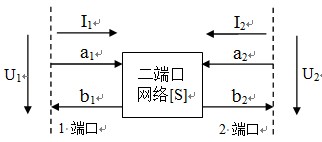
图5 二端口网络示意图
S参量是根据某端口上接匹配负载的情况下所得到的归一化波来定义的。设an表示第n个端口的归一化入射波电压,bn表示第n个端口的反射波归一化电压。
所谓归一化波,就是各端口的波用其对应端口的参考阻抗进行归一化后得到的波,它们与同端口的电压的关系为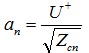 (21a)
(21a)
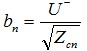 (21b)
(21b)
对于线性二端口网络(如图5所示),归一化入射波a和反射波b之间存在如下关系
b1=S11a1+S12a2 (22a)
b2=S21a1+S22a2 (22b)
式(22)写成矩阵形式为
b=Sa (23)
矩阵S称为二端口网络的散射矩阵或S矩阵,表示为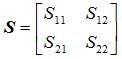 (24)
(24)
式(24)中的矩阵元素称为网络的散射参量,各项矩阵参量的物理意义为:
S11=b1/a1/|a2=0表示端口2匹配时,端口1的反射系数;
S22=b2/a2/|a1=0表示端口1匹配时,端口2的反射系数;
S12=b1/a2/|a1=0表示端口1匹配时,端口2到端口1的传输系数;
S21=b2/a1/|a2=0表示端口2匹配时,端口1到端口2的传输系数;
ai=0表示第i个端口接匹配负载,该端口不存在反射波。
有一点非常重要,就是所有的参量都是在对应负载匹配的情况下定义的,如果对应的负载不匹配,那么相应的反射系数和传输系数就不再等于S参量。
二端口网络有几个重要的特性参量,它们与散射参量也有着密切的关系。
滤波器可以等效为如图6所示的二端口网络。
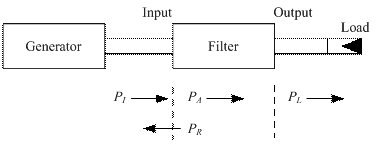
图6 滤波器等效二端口网络
图6中,PI表示入射功率,PR表示反射功率,PA表示吸收功率,根据能量守恒关系,有
PI=PR+PA (25)
通过滤波器的功率被负载吸收称为负载功率PL,显然PL≤PA;如果滤波器无损耗,则PL=PA;如果输入端又无反射,PR=0,则PL=PI。
从源得到的最大入射功率PI为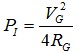 (26)
(26)
而反射损耗LR为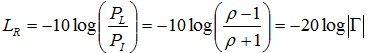 (27)
(27)
其中ρ为驻波系数,Γ为反射系数。
4、谐振与耦合
谐振器是微波滤波器的重要组成部分,微波谐振器与集总参数谐振回路在结构上不同,但是它们的物理本质却完全相同。谐振回路的品质因数Q0都可以定义为
 (28)
(28)
其中ω0为谐振时的角频率,PL为谐振时的功率损耗。
品质因数还可以表示为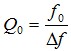 (29)
(29)
Q0越高,谐振器的选择性越好。Q0为无载品质因数,在考虑负载的情况下,即谐振器之间进行耦合时,必然导致系统的品质因数Q0降低。
在串联谐振电路中,负载等效为串联电阻,在并联电路中,负载等效为并联电阻。电路谐振时,损耗在该附加电阻上的功率记为Pe,外观品质因数Qe为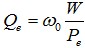 (30)
(30)
与谐振电路的品质因数的定义相类似,微波谐振器品质因数也定义为储能与功耗的比值。仍然用Q0表示空载品质因数,Qe表示外观品质因数,QL表示有载品质因数。微波谐振器谐振时,电储能的最大值We和磁储能Wm的最大值相同,都等于总储能。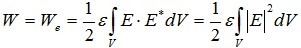 (31a)
(31a)
 (31b)
(31b)
其中ε为介质介电常数,μ为介质磁导率,V为谐振腔体积。
功率损耗包括介质损耗与导体损耗,介质损耗功率Pd为
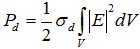 (32)
(32)
其中σd为有损介质的电导率。壁面导体损耗功率Pc为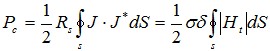 (33)
(33)
其中σ为电导率,S为腔内壁总面积,Rs为导体表面电阻,σ为趋肤深度。
若只考虑导体损耗时,Q0记为Q0c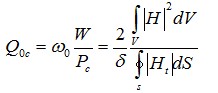 (34)
(34)
若只考虑介质损耗,Q0记为Q0d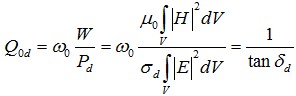 (35)
(35)
其中,tanσd为介质的损耗角正切。
同时考虑介质损耗以及导体损耗,Q0为: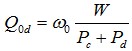 ,由此得出
,由此得出
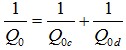 (36)
(36)
对于不同的谐振模式,场分布是不同的,Q值和谐振波长都有所不同,谐振器的Q值和谐振波长都是对于某一特定的振荡模式而言的。
5、本章小结
本章是本文工作的理论基础,介绍了射频滤波器设计涉及到的微波基础理论知识,包括微波传输线理论,微带线理论,二端口网络。在微波传输线理论中介绍了分布参数元件、特性阻抗、电压驻波比等重要概念。介绍了微带射频滤波器设计用到的微带传输线和微波谐振器。介绍了射频电路设计中重要的微波网络理论。

