fdtd非垂直入射问题

求一个用fdtd方法进行仿真的程序。
问题的已知条件是一个正弦波与法线成θ角从空气射入水中，现有的程序为垂直入射。我现在的思路是用坐标变换的方法去解决一维坐标转换便于绘图的问题。
现在解决不了的是当成θ角以后边界条件就不能像垂直入射的一样那么简单了吧。我想求各位大神帮忙教教我关于成角度的问题边界条件怎么加入。最好能有类似问题的程序参考下，谢谢！

 

额，完全没有明白楼主是想说明什么问题呢。
首先，如果你用fdtd来仿真计算的话，那么只不过是离散化成一堆网格，然后不同网格填充不同材料来计算而已。这个时候计算过程还是依赖麦克斯韦方程组（所谓的边界条件不就是积分的麦克斯韦方程组得到的嘛），那么完全没有什么必要去做什么特殊边界啊。
不管是什么角度入射，那也只是你入射的光源不同罢了，它传播中的迭代式还是一样的，不会改变。所以我没有理解你的边界条件是什么意思？
建议楼主如果真想弄明白的话将葛德彪的《时域有限差分算法》的前两章看看，这个结合基本的电动力学知识肯定就可以看懂了。没记错的话，你这个模型其实在光学书上都会有理论解，这种程序都是拿来练练上手才会写的吧。你如果时间充裕不妨自己试试，估计很少会有人特意去写这种程序。

 

fdtd分为一维二维三维，如果用一维的方法去解决斜入射（成角度）的问题就需要用到一些特殊的手段。因为正常的一维问题都是垂直入射的。这么说能听懂？

 

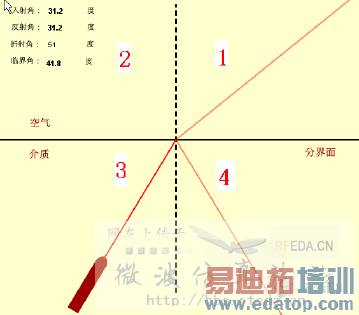
图的分界面应该是哪个虚线。

 

额，如果你有了一定的角度入射还能称之为一维问题吗？囧。这个传播方向都有了两个方向了吧，这个你还是用一维的情况来做的话实在不知道是否合理呢。毕竟你如果用一维的来做的话不管你的边界是如何假定，它都会有在另外两个方向的对称性吧（我的理解就是一维情况只是三维中的一种特殊对称而已），而这个已经不具有两个方向上的对称性了啊。
话说二维FDTD在葛德彪的书上第二章也有较为详细的介绍的，你能够写一维的话拓展到二维应该是不会花太多时间的。有什么问题可以在本站提提交流。

 

我的目的就是用一维的方法来做。

申明：网友回复良莠不齐，仅供参考。如需专业解答，请学习本站推出的微波射频专业培训课程。