关于ADC FFT仿真结果分析
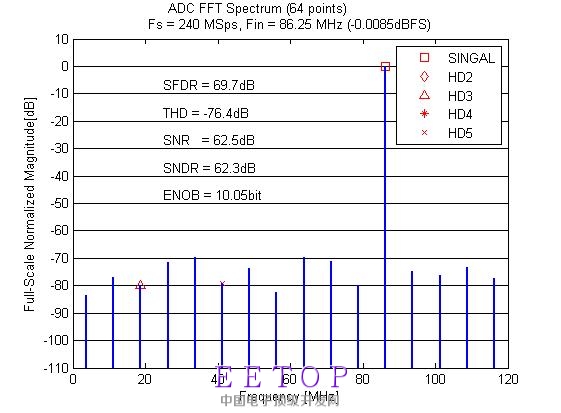
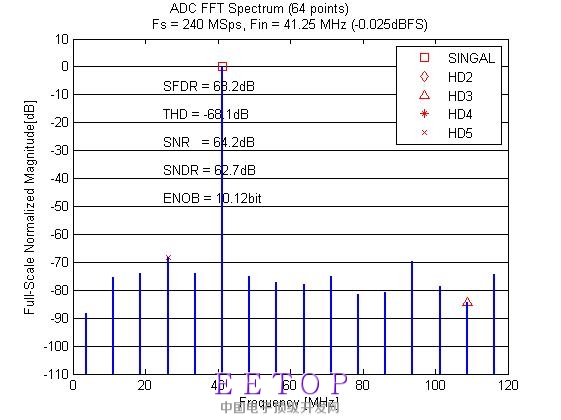
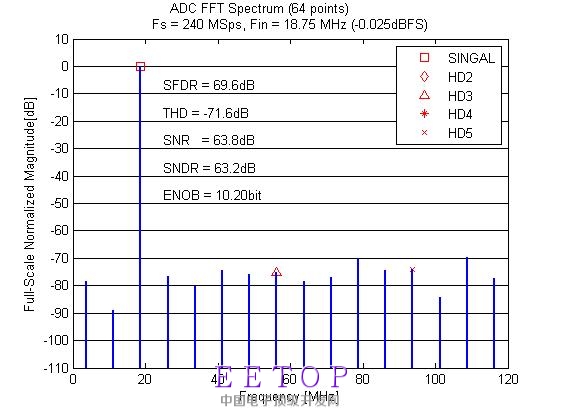
仿真时没有考虑IO pad的寄生影响,主要疑问有:
1、每次出来的ENOB都比10大,SNR值也比理想的要大
2、为什么有的谐波几乎为0,在cadence中我做了DFT,结果也是这样,部分谐波非常小
3、我用理想的8bit ADC做了实验,出来的结果部分谐波也是几乎为0。
下面贴出FFT的程序和理想10bitDAC代码。中间我也尝试着把span、spanh、spandc取了不同的值,但结果几乎一样。
第一次做,求大神指导。非常谢谢!
%***********************************************************************%
% The following program code plots the FFT spectrum of a desired test tone.
% Test tone based on coherent sampling criteria, and computes SNR, SNDR, THD and SFDR.
% This program is believed to be accurate and reliable.
% This program may get altered without prior notification.;
% Company: xxx Analog Mixed-signal Group
% Author:
% Date: 2016-01-09
%***********************************************************************%
%***********************************************************************%
% 采样时钟240MHz,输入信号频率86.25MHz,FFT点数64,ADC分辨率10bit,仿真时间400ns。
% 从cadence输出时间隔是4.16666667ns,共计97个点,从第20个点开始取64点做FFT。
% cadence输出的是归一化的结果范围是0-1.6V,需除以1.6再乘以1024,转换为数字码。
%***********************************************************************%
clear all;
clc;
datafile='ADC_result8.csv'
spectP_file='spec.csv';
%***********************************************************************%
% 输入采样时钟、样本点数、分辨率等变量
%***********************************************************************%
fs=240e6; %采样时钟
Data_Num=64; %样本点数
numbit=10; %ADC分辨率
data_start=20; %取点起始位置
fclk=fs/1e6; %x坐标轴数值显示
numpt=Data_Num;
fres=fclk/numpt; %Desired frequency resolution of FFT[MHz], fres=fclk/2^N
%***********************************************************************%
% 读取数据
%***********************************************************************%
d_in=csvread('ADC_result8.csv',1,1);
d_in=d_in/1.6*1024;
code=zeros(1,numpt);
code(1:numpt)=d_in(data_start:data_start+numpt-1);
%***********************************************************************%
% Plot output code
%***********************************************************************%
figure;
plot(code);
title(sprintf('ADC Digital Output'));
%***********************************************************************%
% Recenter the digital sine wave, for 2's complement code
%***********************************************************************%
m_ean=mean(code);
for hk=1:length(code)
code(hk)=code(hk)-m_ean;
end
%***********************************************************************%
% Display a warning, when the input generates a code greater than
% full-scale, for 2's complement code
%***********************************************************************%
max_code=max(code)
min_code=min(code)
if (max(code)>2^(numbit-1)) | (min(code)<(0-2^(numbit-1)))
%if (max(code)==2numbit -1) | (min(code)==0)
disp('Warning: ADC may be clipping!');
end
%***********************************************************************%
% Normalize input signal relative to full-scale
%***********************************************************************%
fin_dB=20*log10((max_code-min_code)/(2^numbit));
%***********************************************************************%
% 对数据样本加窗函数处理
%***********************************************************************%
% If no window function is used, the input tone must be chosen to be unique and with
% regard to the sampling frequency. To achieve this prime numbers are introduced and the
% input tone is determined by Fin = Fsample * (Prime Number / Data Record Size).
% To relax this requirement, window functions such as HANNING and HAMING (see below) can
% be introduced, however the fundamental in the resulting FFT spectrum appears 'sharper'
%without the use of window functions.
Dout=code';
Doutw=Dout;
% Doutw=Dout.*hanning(numpt);
% Doutw=Dout.*hamming(numpt);
% Doutw=Dout.*blackman(numpt);
%***********************************************************************%
% Performing the Fast Fourier Transform [FFT]
%***********************************************************************%
span=0; %Span of the input frequency on each side; span=max(round(numpt/200),5);
spanh=0; %Approximate search span for harmonics on each side
spandc=0; %Approximate search span for DC on right side
Dout_spect=fft(Doutw);
Dout_dB=20*log10(abs(Dout_spect)); %Recalculate to dB abs(Dout_spect)
spectP=(abs(Dout_spect)).*(abs(Dout_spect)); %Determine power spectrum
maxdB=max(Dout_dB(1+spandc:numpt/2));
fin=find(Dout_dB(1:numpt/2)==maxdB); %Find the signal bin number, DC=bin1
%***********************************************************************%
% Calculate SNR, SNDR, THD and SFDR values.
%***********************************************************************%
fw=fopen(spectP_file,'w'); %write the power soectrum to file
fprintf(fw,'%12.9e\n',spectP);
fclose('all');
%Find DC offset power
Pdc=sum(spectP(1:span));
%Extract overall signal power
idx1=fin-span;
idx2=fin+span;
if(idx1<=0)
idx1 = 1;
end
Ps=sum(spectP(idx1:idx2));
%Vector/matrix to store both frequency and power of signal and harmonics
Fh=[];
%The 1st element in the vector/matrix represents the signal, the next element represents the 2nd harmonic
Ph=[];
%Vector/matrix to store the sampling points responding to the harmonics
Nh=[];
%Ah represents signal and harmonic amplitude
Ah=[];
%Find harmonic frequencies and power components in the FFT spectrum
%For this procedure to work, ensure the folded back high order harmonics do not overlap
%with DC or signal or lower order harmonics , so it should be modified according to the actual condition
for har_num=1:5
tone=rem((har_num*(fin-1)+1)/numpt,1); %Input tones greater than fSAMPLE are aliased back into the spectrum
if tone>0.5
tone=1-tone; %Input tones greater than 0.5*Fsample (after aliasing) are reflected
end
Fh=[Fh tone];
%Check Nh to see the bin of the harmonics
Nh=[Nh round(tone*numpt)];
%For this procedure to work, ensure the folded back high order harmonics do not overlap
%with DC or signal or lower order harmonics
har_peak=max(spectP(round(tone*numpt)-spanh:round(tone*numpt)+spanh));
har_bin=find(spectP(round(tone*numpt)-spanh:round(tone*numpt)+spanh)==har_peak);
har_bin=har_bin+round(tone*numpt)-spanh-1;
Ph=[Ph sum(spectP(har_bin-spanh:har_bin+spanh))];
Ah=[Ah Dout_dB(har_bin)];
end
%Determine the total distortion power, it should be modified according to the actual condition.
Pd=sum(Ph(2:5));
%Determine the noise power
Pn=sum(spectP(1:numpt/2))-Pdc-Ps-Pd;
%Determine the next largest component
spur_max=max(max(spectP(spandc+1:fin-span-1)),max(spectP(fin+span+1:numpt/2)));
spur_bin=find(spectP(1:numpt/2)==spur_max)
%**********************计算动态特性结果**********************%
format; %设置输出格式
SFDR = 10*log10(max(spectP(1:numpt/2))/spur_max); %-fin_dB
THD = 10*log10(Pd/Ps); %+fin_dB
SNR = 10*log10(Ps/Pn); %-fin_dB
SNDR = 10*log10(Ps/(Pn+Pd)); %-fin_dB
ENOB = (SNDR-1.76)/6.02;
%disp('Note: THD is calculated from 2nd through 10th order harmonics.');
%*********************标示信号和谐波位置*********************%
%hold on;
%plot((Nh(2:10)-1).*fres,Ah(2:10)-maxdB+fin_dB,'rs');
% 标示信号
bins=(Nh(1)-1)*fres;
Ahs=Ah(1)-maxdB+fin_dB;
% 标示2次谐波
bin2=(Nh(2)-1)*fres;
Ah2=Ah(2)-maxdB+fin_dB;
% 标示3次谐波
bin3=(Nh(3)-1)*fres;
Ah3=Ah(3)-maxdB+fin_dB;
% 标示4次谐波
bin4=(Nh(4)-1)*fres;
Ah4=Ah(4)-maxdB+fin_dB;
% 标示5次谐波
bin5=(Nh(5)-1)*fres;
Ah5=Ah(5)-maxdB+fin_dB;
% 在FFT频谱图中追加标示
figure;
plot(bins,Ahs,'rs',bin2,Ah2,'rd',bin3,Ah3,'r^',bin4,Ah4,'r*',bin5,Ah5,'rx');
legend('SINGAL','HD2','HD3','HD4','HD5');
%**********************图表显示**********************%
ylabel('Full-Scale Normalized Magnitude[dB]')
xlabel('Frequency [MHz]')
title(sprintf('ADC FFT Spectrum (%g points)\nFs = %g MSps, Fin = %g MHz (%1.2gdBFS)', Data_Num,fs/1e6,(fin-1)*fres,fin_dB));
grid on;
box on;
ylim([-110 10]);
set(gca,'xgrid', 'off');
set(gca, 'GridLineStyle' ,'-');
set(gca,'yTick',[-110:10:10]);
%****************************************************%
%Display the results in the frequency domain with an FFT plot.
for i=0:1numpt/2-1)
hold on;
line([i*fres,i*fres],[-110,Dout_dB(i+1)-maxdB+fin_dB],'LineWidth',2);
hold off;
end
%***********************在图中打印结果***********************%
hold on;
s1=sprintf('SFDR = %4.1fdB\n',SFDR);
s2=sprintf('THD = %4.1fdB\n',THD);
s3=sprintf('SNR = %4.1fdB\n',SNR);
s4=sprintf('SNDR = %4.1fdB\n',SNDR);
s5=sprintf('ENOB = %4.2fbit\n',ENOB);
text(25,-10,s1);
text(25,-20,s2);
text(25,-30,s3);
text(25,-40,s4);
text(25,-50,s5);
hold off;
10bit DAC
`include "discipline.h"
`include "constants.h"
// $Date: 1997/08/28 05:54:36 $
// $Revision: 1.1 $
//
//
//--------------------
// dac_10bit_ideal
//
// - 10 bit digital analog converter
//
// vd0..vd9:
data inputs [V,A]
// vout:
[V,A]
//
// INSTANCE parameters
// vref = reference voltage that conversion is with respect to [V]
// vtrans = transition voltage between logic high and low [V]
// tdel,trise,tfall = {usual}
//
// MODEL parameters
// {none}
module dac_10bit_ideal (vd9, vd8, vd7, vd6, vd5, vd4, vd3, vd2, vd1, vd0, vout);
electrical vd9, vd8, vd7, vd6, vd5, vd4, vd3, vd2, vd1, vd0, vout;
parameter real vref = 1.6 from [0:inf);
parameter real trise = 0 from [0:inf);
parameter real tfall = 0 from [0:inf);
parameter real tdel = 0 from [0:inf);
parameter real vtrans = 0.45;
real out_scaled; // output scaled as fraction of 1024
analog begin
out_scaled = 0;
out_scaled = out_scaled + ((V(vd9) > vtrans) ? 512 : 0);
out_scaled = out_scaled + ((V(vd8) > vtrans) ? 256 : 0);
out_scaled = out_scaled + ((V(vd7) > vtrans) ? 128 : 0);
out_scaled = out_scaled + ((V(vd6) > vtrans) ? 64 : 0);
out_scaled = out_scaled + ((V(vd5) > vtrans) ? 32 : 0);
out_scaled = out_scaled + ((V(vd4) > vtrans) ? 16 : 0);
out_scaled = out_scaled + ((V(vd3) > vtrans) ? 8 : 0);
out_scaled = out_scaled + ((V(vd2) > vtrans) ? 4 : 0);
out_scaled = out_scaled + ((V(vd1) > vtrans) ? 2 : 0);
out_scaled = out_scaled + ((V(vd0) > vtrans) ? 1 : 0);
V(vout) <+ transition( vref*out_scaled/1024, tdel, trise, tfall );
end
endmodule
小编是用理想的behavior model 仿真得到的数据吗?如果是的话,FFT就是如图所示。你这里只取了64点做FFT, quantization noise不能视为均匀分布,会产生的tones。而且你这里没有加noise,所以看不到噪底 。如果增加点数,应该可以看到中间空白处出现新的 tone。关于ENOB的波动,应该还是采样点数太少造成的,因为ENOB = (SNDR - 1.76)/6.02 里面同样假设quantization noise是均匀分布的。
说点粗浅的看法:可能是fft长度不够的原因, 对一个随机信号的进行fft变换的结果应该也是一个随机信号, 所以fft变换的长度决定了fft变换结果的置信度, fft变换长度越长, 得到的频谱越准. 我一般用256点fft.
我做的理想8bit sar adc, 在经过去直流分量处理之后的enob大概是7.98, 12 bit 非理想sar adc模型在只考虑0.1%电容失陪时enob在11.5bit左右, 从没有过enob大于设计值的情况出现.
即使小编所有电路都是线性的, 只要输入信号的均值不是0, 那么不可能得到dc分量为0的输出信号.
小编做fft的时候不能从第20个点开始要从dc开始, 另外输入信号的bin点最好预先指定, 而不是在频谱图里找最大值, 因为这种做法无法展示系统的非线性(当系统是非线性时输入信号和输出信号的频率不同).
谢谢您的分析。1、不是Behavior model,设计里面DAC电容阵列由于单位电容太小,要靠版图寄生实现,所以前仿时用的电容是analog lib里的理想电容。其他模块都是自己设计的。
2、请问关于量化噪声有没有推荐的资料呢?
3、tran仿真的时间变长后,仿真得到的波形是错误的,是要自定义仿真时的step吗?请问该如何设置,所以暂时还没有做更多点的FFT
4、目前查的资料有的说是FFT取点太少造成的,有的说是span spandc spanh设置造成的,也有说是跟我的输入信号频率有关,还有说差零点几个dB很正常?。
请大神赐教,谢谢
谢谢您的分析。1、dc为0的原因是因为我对DAC输出做了归一化处理,把直流分量消除了。
2、看了频谱里的最大值和输入信号的频率是一致的
3、那个是从dc开始的,从第20个点取得意思是在DAC输出时,在cadence中导出数据时考虑到前几十ns的数据可能不准确,所以从第20个点开始取了64点,然后做的FFT,不知道这样做是不是有问题?
4、当tran仿真时间变长以后,得到的波形是错误的,我觉得可能需要自己设定仿真器的步长?不知道是不是这样,还不知道怎么设定step,所以只做了64点的FFT。
非常感谢您的回答。
看了walt Kester的一篇文章似乎懂了一点,要加上处理增益
1. 用输出信号-mean(输出信号)的方式去dc分量我也做了, 不过对摆幅在0-Vref之间的sine信号, 这种方法是不能完全去掉dc的
2. 从第20个点开始取值是正确的, 但前提是你的信号在第二十个点时已经稳定了
3. 仿真时间变长后, 得到波形错误, 这种情况我还没遇到过. 不过我遇到过瞬态仿真步长太小不能收敛的问题. 我想是不是你要查查你的电路?
4. process gain 影响噪底, 你取256个点试试.
您好,1、又思考了一下,感觉应该也不是process gain的问题,因为虽然会和输入信号频率有关,但是我计算信噪比时取的噪声还是0--fs/2之间的。所以应该是我的电路的问题。
2、做了256点的FFT结果还是一样
3、那个tran输出波形的确是我的step和maxstep取的不合理,修改之后可以得到正确波形了。
4、那个dc分量确实不为零,但是几乎为零了,由于显示精度的问题,所以看着几乎为零。
麻烦您了。
请教一下小编,
你去的信号频率96.25,41.25,18.75MHz,用240M信号采样64给点没有办法取到整数周期啊?
您好,不知道您是不是这样算的,18.75/240=5/64,正好在5个周期采了64个点,是这样的吗?
哦,我算错了。谢啦
我做了个ADC
算出来的SNR也是高于理想值的,跟小编的情况一样
我在仿真当中还没有加入噪声,所以应该不能用walter kester那个公式来解释
另外那个公式前提是信号有被滤波,带外噪声被压制了
仿真当中应该都是理想sin 没有被滤波吧
在论坛上也见其他人有相似的疑问,刚还发了一贴求助,期待大神回答,我的偶次谐波都非常小的,不知道您的是否有这样的情况?我用理想的AD+DA仿真了一下也得到了同样的结果。您说的那个应该是过采样的问题吧,需要再接一个滤波器把噪声限制在一定范围内才会用高于理想值的情况,可是我算的是0--fs/2内的噪声,也出现了这种情况,就不知道怎么解释了
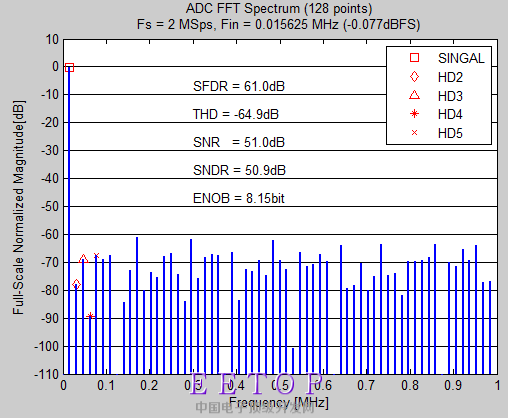
我的8bADC, 用你的matlab code跑的结果
只有加了窗函数我才会出现偶次谐波
你把输入信号频率提高试试,这频率太低了
我等下试试
频率低会有什么问题?
申明:网友回复良莠不齐,仅供参考。如需专业解答,请学习本站推出的微波射频专业培训课程。

