这个SC积分器的传递函数？

C2和C3明显是有区别的，最重要的一点就是C2的上极板在相位1和2中都要严格遵守电荷守恒，但是C3的上极板在相位1时不需要，因为连接点是真实地而不是虚地。我刚才按照电荷守恒推导得出的表达式和图上那个是一样的，你可以在试试看。

    您看一下我的推导哪里出错了，万分感激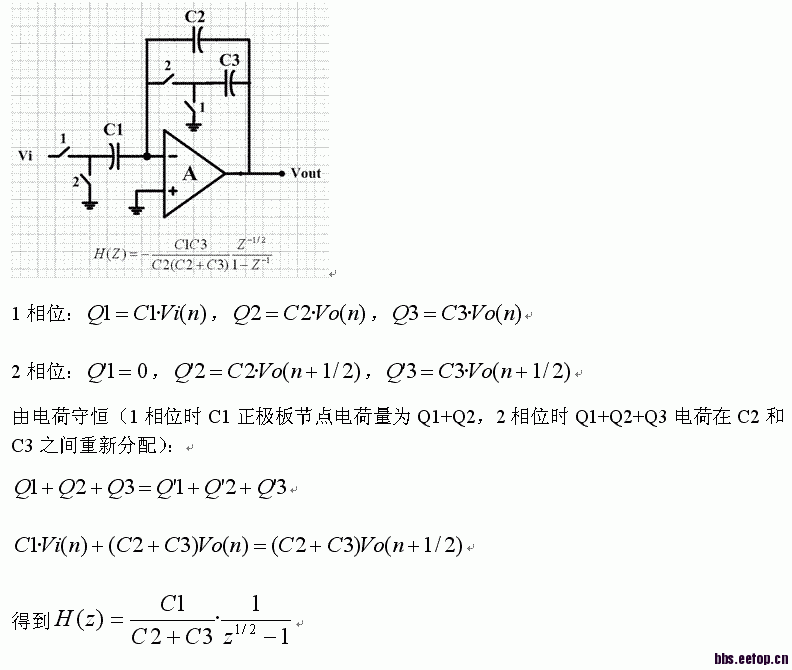

今天时间来不及了，要下班了。明天早上我给你贴个我的推导好吗

今天时间来不及了，要下班了。明天早上我给你贴个我的推导好吗

    谢谢谢谢！我自己总是找不出错误的原因

我也推不出，哎！ 电荷守恒

假设相位1是n-1到n-1/2，相位2是n-1/2到n
Phase 1: C1×Vin[n-1/2]+C2×Vout[n-1/2]=C2×Vout[n-1]
Phase 2: C1×Vin[n-1/2]+C2×Vout[n-1/2]+C3×Vout[n-1/2]=(C2+C3)×Vout[n]
把Vout[n-1/2]消去就能得到结果了。
你的那一步对相位2推导是对的，但是还要一个针对相位1的式子，那就是因为在相位1时C3的上极板切换到运放的输出端的，所以在运放输入端虚地点，C1和C2上极板的总电荷只能等于的C2上极板在上一个相位2时建立起来的电荷。

假设相位1是n-1到n-1/2，相位2是n-1/2到n
Phase 1: C1×Vin[n-1/2]+C2×Vout[n-1/2]=C2×Vout[n-1]
Phase 2: C1×Vin[n-1/2]+C2×Vout[n-1/2]+C3×Vout[n-1/2]=(C2+C3)×Vout[n]
把Vout[n-1/2]消去就能得到结果了。
你的那一步对相位2推导是对的，但是还要一个针对相位1的式子，那就是因为在相位1时C3的上极板切换到运放的输出端的，所以在运放输入端虚地点，C1和C2上极板的总电荷只能等于的C2上极板在上一个相位2时建立起来的电荷。

    谢谢您花这么多心思帮助。明白您的意思了

    是不是可以理解为，相位2到相位1时，由于C3的上极板连接到了实地，所以C3的上极板电荷被传输到地，并不参与电荷转移，因此虽然相位2时，运放的-端的电荷总数是-Vout(n-1)(C2+C3),实际上当相位1来的时候，只有C2的上极板进行了再分配。

对的

请问你这图是仕么论文/书上的啊，谢谢

楼上的推导，在phase1的时候是认为从（n-1）到（n-1/2）C3的电荷保持不变吗?

申明：网友回复良莠不齐，仅供参考。如需专业解答，请学习本站推出的微波射频专业培训课程。