技术牛人详解矢量信号分析仪原理

测量过程的第一个阶段称为信号调整。这个阶段包括几个重要的功能，对信号进行调整和优化，以便于模拟- 数字转换和 FFT 分析。第一个功能是AC 和 DC 耦合。如果您需要移除测量装置中无用的 DC 偏置，就必须使用这一项。接下来信号被放大或衰减，以达到混频器输入的最佳信号电平。混频器阶段提供信号频率的转换或射频到中频的下变频，并将信号最后混频为中频。

这一操作与扫描调谐分析中的超外差功能相同，将 FFT 分析能力扩展到微波频段。实际上，要获得最后的中频频率，可能需要经过多个下变频阶段。有些信号分析仪提供外部 IF 输入能力 ; 你可以通过提供自己的 IF，延展 VSA 的频率上限范围，从而与自己提供的接收机相匹配。

信号调整过程的最后阶段是预防信号混叠，它对于采样系统和 FFT 分析极为重要。抗混叠滤波执行这一功能。如果 VSA 测量没有对混叠做出足够的预防，那么它可能会显示不属于原始信号的频率分量。采样定律告诉我们，如果信号采样速率大于信号中最高频率分量的两倍，被采样的信号就可以被准确重建。最低的可接受的采样率称为奈奎斯特 (Nyquist) 采样率。

因此，ƒs > 2 (ƒmax)
其中 ƒs = 采样率
ƒmax = 最高频率分量

如果违反了采样定律，就会得到“混叠的”错误分量。因此，为了预防所给最大频率出现混叠结果，在 1/2 采样率以上不能有太大的信号能量。频率较高的波形违反了采样定律。

除非使用抗混叠滤波器，否则这两个频率在进行数字处理时将会混淆。为了预防混叠，必须满足两个条件 :

1. 进入数字转换器 / 采样器的输入信号必须是带限的。换句话说，必须存在一个最大频率 (ƒmax)，没有任何频率分量高于这个频率。

2. 必须以符合采样定律的速率对输入信号进行采样。

解决混叠问题的方案看起来很简单。首先选择前端硬件将要测量的最大频率 (ƒmax)，然后确保采样频率 (ƒs) 是该最大频率的两倍。这个步骤满足了条件 2，并确保 SA 软件能够对感兴趣的频率进行精确分析。接下来插入低通滤波器 ( 抗混叠滤波器 )，以去除高于 ƒmax 的所有频率，从而确保除了感兴趣的频率进行测量以为，其它频率都被排除。这个步骤满足条件 1，并确保对信号的带宽进行了限制。

有两个因素会导致简单的抗混叠方法复杂化。第一个也是最容易解决的因素是，抗混叠滤波器的滚降 (roll off) 速率是有限的。如图 6 所示，在实际滤波器的通带和截止带之间有一个过渡带。这个过渡带中的频率可能产生混叠。为了避免这些混叠分量，滤波器的截止频率必须低于理论频率上限 ƒs/2 。

解决这个问题的简单办法是使用过采样 ( 以高于 Nyquist 采样率的速率进行采样 )。使采样频率略高于 ƒmax 的两倍，也就是截止带实际开始频率的两倍，而不是要测量的频率的两倍。许多 VSA 的实现都使用保护带以防止显示混叠的频率分量。FFT 计算超出 50% ƒs ( 相当于 ƒs/2) 的频谱分量。保护带大约在 ƒs 的40% 至 50% ( 或 ƒs/2.56 至 ƒs/2) 之间并且没有显示，因为它可能被混叠分量破坏。不过当 VSA 软件进行逆 FFT 运算时，在保护带中的信号用于提供最精确的时域结果。高滚降率滤波器再结合保护带，会抑制潜在的混叠分量，并将它们衰减到远低于测量前端的底噪。

另一个致使混叠预防 ( 有限的频率分辨率 ) 复杂化的因素解决起来难得多。首先，为宽频扫宽 ( 高采样率 ) 设计的抗混叠滤波器不适用于测量小分辨率带宽，原因有二个 : 一是需要极大的样本数量 ( 内存分 )，二是需要惊人的 FFT 计算量 ( 长测量时间 )。例如，当采样率为 10 MHz 时，一个 10 Hz 分辨率带宽的测量将需要超过 100 万点的 FFT，也就是需要使用巨大容量的存储器和极长的测量时间。这是不可接受的，因为小分辨率带宽的测量能力是 VSA 的一大优势。

提高频率分辨率的一个方法是减小 ƒs，但代价是降低了 FFT 的频率上限，也就是最终分析仪的带宽。不过，这仍不失为一个好方法，因为它允许你控制测量分辨率和频率范围。当采样率降低时，抗混叠滤波器的截止频率也必须降低，否则就会发生混叠。一种可能的解决方案是对每个扫宽提供一个抗混叠滤波器，或提供一个可选择截止频率的滤波器。使用模拟滤波器实现这种方案的困难很多，而且成本高昂，但是有可能通过 DSP 以数字形式添加额外的抗混叠滤波器。

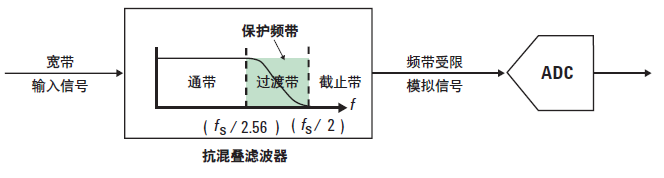
图 6. 抗混叠滤波器衰减高于 ƒs/2 的信号。屏幕上不显示介于 40% 至 50% ƒs 之间的保护带。

数字抽取滤波器和重采样算法提供了频率分辨率受限制问题的解决方法。 Agilent VSA 软件中就使用了这种方法。数字抽取滤波器和重采样执行必要的操作以允许改变扫宽和分辨率带宽。数字抽取滤波器同时降低采样率并限制信号的带宽 ( 提供混叠预防 )。输入数字滤波器的采样率为 ƒs; 输出该滤波器的采样率为 ƒs/n，其中“n”是抽取因子，为整数值。类似的，输入滤波器的带宽为“BW”，输出滤波器的带宽为“BW/n”。许多实现过程执行二进制抽取 ( 采样率按 1/2 的速度降低 )，这意味着采样率按 2 的整数幂改变，即步进值为 1/(2n) (1/2、1/4、1/8......)。通过“除以 2n”得出的频率扫宽称为基数扫宽。由于减少了 DSP 操作，通常在基数扫宽上进行的测量比在任意扫宽上进行的测量要快。

抽取滤波器允许采样率和扫宽以 2 的幂次改变。要获得任意扫宽，采样率必须是无限可调的。这由抽取滤波器之后的重采样或插值滤波器来完成。

尽管数字重采样滤波器在降低采样率的同时提供了混叠的预防，模拟抗混叠滤波器仍然是必要的，因为数字重采样滤波器本身也是一个被采样系统，必须被防止出现混叠。模拟抗混叠滤波器运行于 ƒs 上，保护最宽频率扫宽上的分析。在模拟滤波器之后的数字滤波器，为较窄的、用户定义的扫宽提供抗混叠能力。

当抗混叠涉及带限信号，并使用示波器作为 VSA 软件前端时，还必须采取额外的预防措施。

下一个限制小分辨率带宽分析的复杂因素来源于 FFT 算法自身的本质特性 ; FFT 实质上是一个基带转换。这意味着 FFT 频率范围从 0 Hz ( 或 DC) 开始，一直到某个最大频率 (ƒs/2) 结束。在小频段需要被分析的测量情况中，这可能是一个重大限制。例如，如果测量前端的采样率为 10 MHz，频率范围将从 0 Hz 到 5 MHz (ƒs/2)。如果时间样本数量 (N) 为 1024，那么频率分辨率将为 9.8 kHz (ƒs/N)。这意味着接近 9.8 kHz 的频率可能无法分辨。

如前所述，可以通过改变采样率来控制频率扫宽，但是由于扫描范围的起始频率是 DC，所以分辨率仍然受到限制。频率分辨率可以任意提高，但是付出的代价是最高频率的降低。这些限制的解决方法是带宽选择分析，又称为“缩放操作”或“缩放模式”。缩放操作使您可以在保持中心频率不变的情况下减小频率扫宽。这点非常有用，因为你可以分析和查看远离 0 Hz 的小频率分量。缩放操作允许你将测量焦点放在测量前端频率范围内的任意频率点处 ( 图 7)。

缩放操作是一个数字正交混频、数字滤波和抽取重采样的过程。感兴趣的频率扫宽与缩放扫宽中心频率 (ƒz) 上的复数正弦波与相混频，从而使频率扫宽下变频到基带 ; 然后针对该特定扫宽对信号进行滤波和抽取 重采样，移除所有带外频率。这就是在 IF ( 或基带 ) 上的频带转换信号，有时称为“缩放时间”或“IF 时间”。也就是说，它是信号的时域表示应为它出现在接收机的中频带。在本章结尾的“时域显示”部分我们将对缩放测量做进一步讨论。

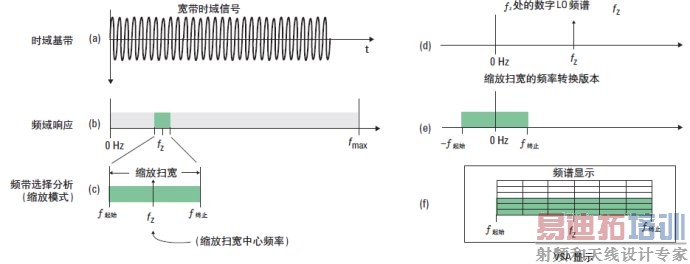
图 7. 频带选择分析 ( 或缩放模式 ): (a) 被测宽带信号，(b) 被测信号的频谱，(c) 选择的缩放扫

宽和中心频率，(d) 数字 LO 频谱 ( 位于缩放中心频率处 )，(e) 频率扫宽下变频到基带，(f) 显
示频谱注释经过调整，以显示正确的扫宽和中心频率

样本存储器

数字抽取滤波器的输出代表的是带宽受限的数字化的模拟时域输入信号。这个数字数据流被捕获到样本存储器中 ( 图 4)。样本存储器是一个循环的 FIFO ( 先进先出 ) 的缓存器，它收集单个的数据采样，形成被称作时间记录的数据块，再由 DSP 进行进一步数据处理。填充时间记录所需的时间长度与并联滤波器分析中的初始建立时间类似。样本存储器所收集的时间数据是用来产生各个测量结果 ( 无论是频域、时域或调制域 ) 的基础数据。

时域数据校正

为了提供更精确的数据结果，VSA 软件通过均衡滤波器进行时间数据校正。在矢量分析中，时间数据的精度非常重要。它不仅是所有解调测量的基础，还直接用于诸如瞬时功率随时间变化的测量中。时间数据校正是创建接近理想的频带限制信号过程中的最后一步。虽然数字滤波器和重采样算法提供了任意带宽 ( 采样率和扫宽 ) 的支持，但是时域校正决定信号路径的最后通带特性。如果模拟和数字信号路径是理想的，那么就没有必要进行时域校正。时域校正起均衡滤波器的作用，以补偿通带内的缺损。这些缺损来源于多处。射频部分中的 IF 滤波器、模拟抗混叠滤波器、抽取滤波器和重采样滤波器都会对所选扫宽内的通频段纹波和相位非线性特性有所贡献。

在设计均衡滤波器时，首先要基于测量前端的配置，从自校准数据中提取关于模拟信号路径的信息。使用这些数据产生频域校正输出显示结果。一旦计算出模拟校正矢量，结果将被修改以便把抽取和重采样滤波器的影响包括在内。

最后频率响应的计算在选定了扫宽后进行，因为它决定了抽取滤波阶段的数量和重采样率。复合的校正矢量充当适用于时间数据的数字均衡滤波器的设计基础。

FFT 假设将要处理的信号从一个时间记录到另一个是周期性的。但大部分信号不是按时间记录周期重复的，两个时间记录之间会出现不连续。因此，这个 FFT 假设条件对大多数测量是无效的，必须假设存在不连续性。如果信号不是按时间记录周期重复，那么 FFT 将不能准确估算频率分量。最终的效果是产生所谓的“泄漏”现象，就是能量从单一频率扩散到一段广泛的频率上。模拟扫频调谐信号分析在扫描速度对于滤波器带宽来说太快时将产生类似的幅度和扩散误差。

数据窗是解决泄漏问题的一个常用方法。FFT 并不是误差的起因，它能够对时间记录中的信号生成“精确”的频谱。导致误差的罪魁祸首是时间记录之间的非周期性信号特性。数据窗使用窗功能修改时域数据使其变成按时间记录为周期。实际上，它强迫波形在时间记录的两端变成零。这由给时间记录乘以加权的窗函数来实现。窗对时域中的数据进行变形，以改善其在频域中的精度。参见图 8。

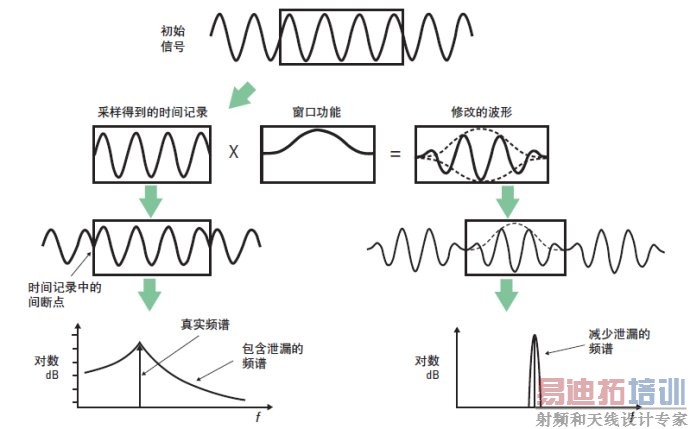
图 8. 窗功能通过修改时域波形，减少频域中的泄漏误差。