傅立叶变换的简易指南

让我们看看每个时间点：

在0时刻，每个周期函数都处于最大值，（4？？？）由4个周期函数（0Hz 1Hz 2Hz 3Hz）叠加而成，每个函数的幅值都是1，而相位角都为0（换言之， 1 + 1 + 1 + 1 = 4）。

在之后的时刻（t = 1， 2， 3），所有周期函数的幅值必须相互抵消。

下面是数值为0的秘诀：当周期函数的值处于对称轴的两端（南和北，东和西，等等。），它们的和为0（要是3个周期函数均匀的分布在0，120和240度，它们就能相互抵消）。

想象许多绕圈旋转的点。先面试每个点在每个时刻的位置：

　　时刻 0 1 2 3

　　------------

　　0Hz:0 0 0 0

　　1Hz:0 1 2 3

　　2Hz:0 2 0 2

　　3Hz:0 3 2 1

要注意，3Hz的周期信号从0开始，然后到了3，然后到了6（只有4个位置，6Mod，然后是9（9Mod4=1）。

每个周期长度为4个单位，周期函数在2个单位时的位置既不在一条线上（不同于0， 4， 8…），也不再相反的位置（不同于2， 6， 10…）。

好了。让我们看看每个时间点的情况：

时刻 0：所有的周期函数都处于最大值（其和为4）
时刻 1：1Hz和3Hz函数值相互抵消（位置1和3是相反的值），0Hz和2Hz函数值相互抵消。最后结果为0.
时刻 2：在0时刻，1Hz和3Hz函数值相等，在2时刻，0Hz和2Hz函数值相等（相反的值）。相加结果还是0.
时刻 3：0Hz和2Hz函数值相互抵消.1Hz和3Hz函数值相互抵消。
时刻4（重复时刻0的情况）：所有函数值相等。

秘诀在于让相互独立的函数相互抵消（0Hz 和 2Hz， 1Hz 和 3Hz），或是让同方向上数值和相互抵消（0Hz + 2Hz 和 1Hz + 3Hz）。

当每个周期属性相等，相位为0时，就可以对齐并消去后面的值。（我并不能很好的证明这一点——有人能吗？——但你可以自己看到其发生。试试［1 1］， ［1 1 1］， ［1 1 1 1］，你会注意到一个脉冲波峰：（2 0）， （3 0 0）， （4 0 0 0））。

这里直观的显示了怎么对齐，接下来是消去相反值：

　

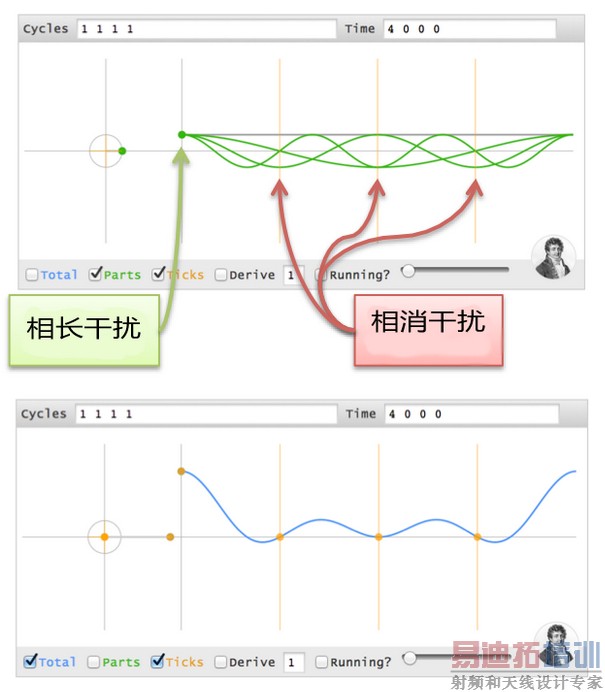
改变峰值时间

t=0时，什么都没有发生。接下来换到（0 4 0 0）？

应该和（4 0 0 0）看起来差不多，但是周期函数必须在t=1时（当前时刻的1s后）对齐。然后要考虑相位。

想象有4个人参与的赛跑。赛跑开始时，4个人都在起跑线上，（4 0 0 0）。没意思。

怎么能让每个人都同时到达终点呢？很简单。只要让他们不停的你追我赶就行了。也许奶奶在终点线前两英尺，Usain Bolt离线还有100米，他们可以拉着手一起穿过终点线。

相位变化，起始角度就是周期信号世界里的延迟。接下来要说怎么调整起始位置，来者每个周期都延迟1秒：

0Hz周期函数不发生移动，所以它已经对齐了

1Hz函数在4秒完成一次往复，所有延时一秒意味着1/4轮。相位延迟90度（-90），然后它在t=1时刻到达相位0，其最大值。

2Hz函数的变化速度是1Hz函数的两倍，所以要两倍的角度来满足要求（-180或180，分别沿着不同的方向）。

3Hz函数的速度是1Hz函数的3倍，所以要有3倍的移动距离（-270或90度的相位改变）

如果时间点（4 0 0 0）是由函数［1 1 1 1］产生，那么（0 4 0 0）则是由［1 1：-90 1:180 1:90］产生。（ 注意： 此处用1Hz来表示一个周期运动经过的时间）。

天呐——我们在脑子里算出了周期函数！

干扰可视化是与之类似的，除了要在t=1时刻进行对齐。
 

　　

试一下这个：你能想象出（0 0 4 0），即2秒延时时候的情况么？0Hz没有相位。1Hz是180度，2Hz是360度（也就是0度），3Hz是540度（即180度），结果为［1 1:180 1 1:180］。

完整的傅立叶变换

事实上：我们的信号只不过是一大堆脉冲信号的叠加！只要得到每个时刻组分，你就能知道整个信号的成分。

傅立叶变换通过频率得到“配方”：

把连续的信号（a b c d）分成不同的时刻：（a 0 0 0） （0 b 0 0） （0 0 c 0） （0 0 0 d）

任意频率（例如2Hz），试验配方是“a/4 + b/4 + c/4 + d/4“（每个尖峰的强度被除以频率数目）

等等！还要对每个脉冲设置延时（每一秒延时的角度取决于频率）。

每个频率真正的配方=a/4 （无延时） + b/4 （1秒延时） + c/4 （2秒延时） + d/4 （3秒延时）。
遍历每个频率就能得到完整的变换结果。

这就是从“数学文字”到真正数学的过程：
 

　　
 

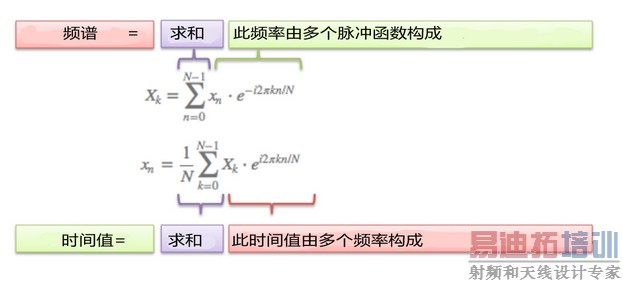
几个要点：

• N=时间样本的数量

• n=当前运算的样本编号（0 。。 N-1）

• xn=n时刻信号值

• k=当前频率（0Hz到N-1Hz）

• Xk=信号中频率k的值（幅度和相位，一个复数）

1/N被用于反变换（从时域信号转化为频域信号）。这是可以实现的，尽管我更喜欢用1/N进行正变换，它表示了脉冲信号的正真大小。你也在变换过程（正反变换中仍含有1/N）中使用1/sqrt（N）。

n/N是我们经过的时间比例。2πk是单位为弧度/秒的速度，e^-ix是反向经过的路径。合起来就是以当前时间和速度经过的实际路程。

傅立叶变换的原始方程只告诉你“加上复数”。很多变成语言并不支持直接使用复数，因此要把它们转化成直角坐标系，然后相加。


让我们开始吧

这是我遇到的最有挑战性的课题。傅立叶变换涵盖了几个要点（离散/连续/有限长/无限长）的高深数学（狄拉克δ函数），很容易遗漏掉一些细节。这真的很挑战我的认知。

但仍有简单的类比来说明这些——我拒绝用别的方式思考。无论是思暮雪还是Usain Bolt & Granny穿过终点线，都能让我们轻易的理解这一点。这个比喻是有缺陷的，但不算坏：它是一个木筏使用，一旦我们过河就把它们留下。

我意识到我自己的理解是如何薄弱，我没办法在自己的脑海里想出（1 0 0 0 ）的变换。对我来说，就像，我懂加法。但是，“1+1+1+1”到底等于几呢？为什么不呢？难道这些最简单的运算不该有个直观的展示么？