模拟电路设计(十四)OP增幅电路异常波动原因与对策
录入:edatop.com 点击:
前几篇曾经介绍只要施加负归返(return),就能够使OP增幅电路稳定动作,不过实施上OP增幅电路经常出现动作不稳定或是波动等现象,因此本文要探讨OP增幅电路容易发生动作不稳定的原因,以及如何进行有效对策。
增幅电路波动条件 ‧OP增幅器波动时的波形
图1是观察OP增幅器输出波形获得的结果,根据波形显示可以判断该OP增幅器可能发生波动现象,因为图1(a)显示输出信号中有相同的高频振盪波形重叠,而图1(b)则显示部份输出波形中则有振盪波形重叠;即使将图1(c)的ground作短路,也会出现大振幅的波动波形。
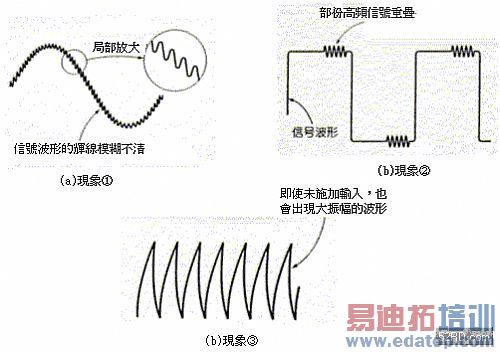 图1 OP增幅器波动时的波形
‧造成波动的条件 (Aβ=-1)
环绕归返loop一圈后的输出信号Vout,与元信号Vout1的level相等而且位相相同时,OP增幅器若施加负归返,就会产生如图2所示的波动,造成这种现象主要原因是元信号在归返电路被分压,接着信号折返OP增幅器的反相输入端子所致;反之若是正常状况,输出信号的位相会对元信号作1800旋转,不过输出信号的位相若旋转超过1800变成与元信号相同位相,而且是相同level的话,同样也会发生波动,此时必需切割归返电路并从外部施加Vout1,如此便可以输出Vout。由于位相与level两者相同,因此若将切割后的归返电路如果再度连接的话,即使未从外部施加Vout1,也会持续输出Vout进而引发波动。以上关系可用下式表示: Aβ=-1----------------------------------------(3)
A:OP增幅器的open loop gain。
β:归返率(return rate)。
式中的Aβ称为loop gain。从式(3)可知loop gain的大小为1,位相旋转-1800时就会产生波动。图2中的式(5)为波动的条件,虽然它是以-1800为基准,不过它是位相为高频延迟所造成;反之即使是+1800 (=1800+3600)就会造成任何不良影响,因此一般是以该值当作设计基准。 ●即使位相旋转1800在|Aβ|<1也不会波动
所谓负归返是指|Aβ|的位相旋转比1800更小时的动作模式(mode)而言,这种情况通常不会发生波动。值得注意的是位相旋转1800时的动作模式称为正归返(return),而不是上述的负归返,此时如果|Aβ|<1的话,正归返的信号则会逐渐衰减,因此即使类似over shoot 等暂时性的异常输出,也不造成电路波动。
●位相旋转1800而且|Aβ|≥1时,就会发生波动
位相旋转1800时,如果|Aβ|=1的话,OP增幅器就会发生波动;|Aβ|≥1时在OP增幅器内部会产生clip,gain,而gain A则大幅降低,其结果造成|Aβ|=1持续波动,图1(c)就是电路发生波动时的典型波形。 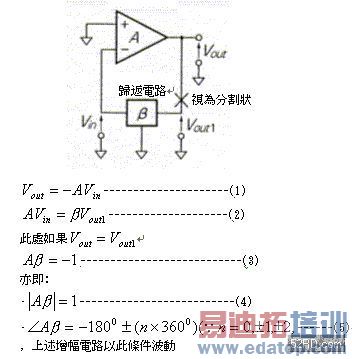 图2 OP增幅器的波动条件 设计不会波动增幅器的基本技巧
‧利用Vote判断是否会波动
具体方法是根据OP增幅器产生动增的条件,再利用图3所示的loop gain传达关数 的Vote线图,检视负归返环绕电路一周后的gain,藉此判断gain与位相是否有充分的裕度,负归返稳定度可以利用下列gain裕度与位相裕度作判定:
●gain裕度
如图3(a)所示,读者可以从位相变成1800的频率中,轻易找出有多少loop gain 因|Aβ|(1倍)变成负,该负值就是所谓的gain裕度。如果gain裕度是正的话,表示电路可能会产生波动现象。
●位相裕度
如图3(b)所示,读者可以从loop gain|Aβ|变成0dB(1倍)的频率中,找出有多少位相因-1800变成内环。上述位相与-1800的差称为位相裕度,如果位相与-1800两者的差大于-1800的话,表示电路可能会产生波动现象。 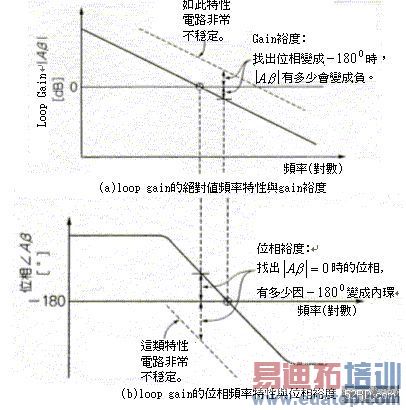 图3 OP增幅器的位相裕度与Gain裕度 ‧位相裕度与Gain裕度的最佳值
表1是位相裕度与Gain裕度的最佳经验值一览表。一般增幅电路要求位相裕度能够超过600,定电压电源则希望能够超过450以上。然而实际上裕度太小的话,电路的稳定度会降低,相反的如果裕度太大时,基于各种原因loop gain会变小,gain误差则变大,反应速度随着变慢。 | Gain裕度 | 位相裕度 | 特徵 | | 3dB | 200 | 发生严重的linking | | 5dB | 300 | 发生轻微的linking | | 7dB | 450 | 反应时间很短 | | 10dB | 600 | 一般适用值 | | 12dB | 720 | 频率特性无法出现peak |
表1 相裕度、Gain裕度与step反应
‧二次延迟电路容易发生波动
大部份的OP增幅器都属于二次延迟电路。前几篇介绍的OP增幅IC单体的open loop gain频率特性,大多属于近似性的一次延迟特性,然而实际上大部份的OP增幅IC的open loop gain为1,频率特性fr则属于二次延迟特性,即使是fr以下的频率因寄生阻抗(impedance)造成的延迟,它的频率也是属于二次延迟特性。由于一次延迟电路的位相回转角度最大值是-900,因此只要将两个一次延迟电路连接的话,就可以构成二次延迟电路,此时位相回转角度在无限大频率时会增加变成-1800 。
在有限频宽下动作的二次延迟电路,理论上只要施加负载就会变得非常稳定,不过因为有寄生阻抗造成的延迟问题,因此实际上电路仍然非常不稳定,这意味着电路有可能产生波动现象。
‧二次延迟电路负归返的反应
图4是可以显示二次延迟特性的增幅电路负归返时的传达关数。图中的![]() (zeter)称为制动系数,它是非常重要的参数(parameter)请读者务必牢记。传达关数 可根据图下方的公式整理成: (zeter)称为制动系数,它是非常重要的参数(parameter)请读者务必牢记。传达关数 可根据图下方的公式整理成:
![]()
由图4可知,一旦施加负归返不论是T或是![]() ,都会减少成为无归返的 ,都会减少成为无归返的![]() ,也就是说只要施加负归返,下列现象就会成立: ,也就是说只要施加负归返,下列现象就会成立:
(a).![]() 若变小时,输出就不易制动,电路变成不稳定的可能性相对变高。 若变小时,输出就不易制动,电路变成不稳定的可能性相对变高。
(b).T若变小时,2ΠT的关数亦即频宽就会变大。
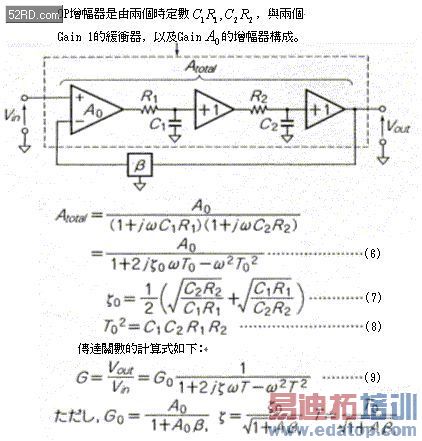 图4 可以显示二次延迟特性的增幅电路负归返时的传达关数
●![]() 与step的反应(response) 与step的反应(response)
图5是将![]() 视为参数(parameter),当loop gain变成1的时,频率fc附近的传达特性。图6是将step的反应与 视为参数(parameter),当loop gain变成1的时,频率fc附近的传达特性。图6是将step的反应与![]() 视为参数时的over shoot比率,它是将式(9)的传达关数jω设为s,再作Laplace转换获得的结果。 视为参数时的over shoot比率,它是将式(9)的传达关数jω设为s,再作Laplace转换获得的结果。
![]() =1时称为临界制动,它是未出现over shoot时的界限值,此时的频率特性在滤波电路称为vessel特性; =1时称为临界制动,它是未出现over shoot时的界限值,此时的频率特性在滤波电路称为vessel特性;![]() >1时称为过制动,虽然它不会出现over shoot,不过反应速度却很慢; >1时称为过制动,虽然它不会出现over shoot,不过反应速度却很慢;![]() <1时称为制动不足,此时会出现over shoot; <1时称为制动不足,此时会出现over shoot;![]() = =![]() 时虽然会出现over shoot,不过此时的gain频率特性最平稳,该频率特性滤波电路称为butter worth特性。 时虽然会出现over shoot,不过此时的gain频率特性最平稳,该频率特性滤波电路称为butter worth特性。
●根据step的反应判断频率特性
验证增幅电路的频率特性时,有时也会利用方形波,主要理由是图5与图6两者具有关连性,例如在step信号当t<0时电压会变成0,不过在方形波却呈连续状,因此可以忽略t<0的影响,利用频率进行观测。
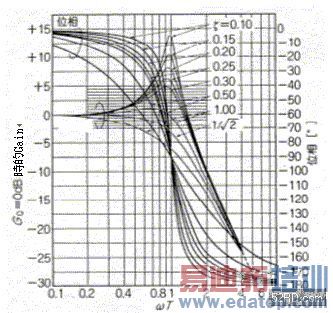 图5 loop gain变成1时频率特性附近的传达特性 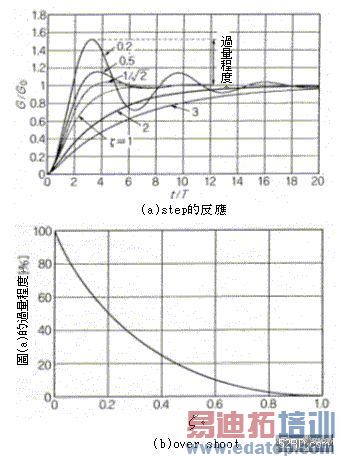 图6 step的反应与![]() 视为参数时的over shoot比率 视为参数时的over shoot比率
| | |
如何设计不会波动增幅器
(一).消除输入容量造成的不稳定动作
‧输入容量会使位相延迟,同时还会使电路的稳定度降低
如图7(a)所示容量C1若附加于OP增幅器的话,会立刻发生位相延迟现象;如图7(b)与7(c)所示,即使根据β与Aβ的Vote线图追加设置C1,电路依旧会出现二次延迟特性,同时变成不稳定状态。
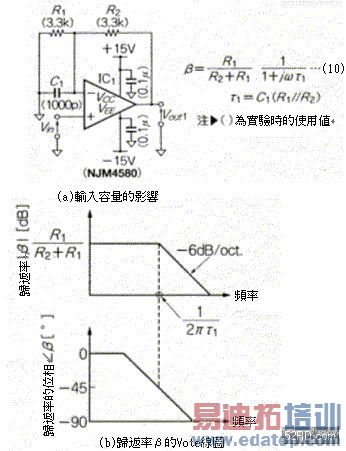
![]() 图7 容量C1附加于OP增幅器时的Loop Gain特性
‧使容量相同的电容归返并作补偿
图8(a)是位相延迟的补偿方法。假设:
R1:R2=Ccomp:Cin------------------------------(11) 如此一来位相延迟就可以获得完全补偿。接着使图7(a)与图8(a)的电路实际动作,藉此确认位相延迟的补偿效果。照片1是输入方形波的反应波形,由照片可知相较于未补偿的Vout1波形,已经补偿的Vout2波形over shoot几乎完全消失;如果Ccomp=100pF时,波形会变得非常迟钝,造成波形迟钝的主要原因是OP增幅器的特性所致;如果Ccomp=47pF时,波形迟钝会被over shoot抵消,虽然输出几乎没有任何的迟钝现象,不过却会出现少许的linking。 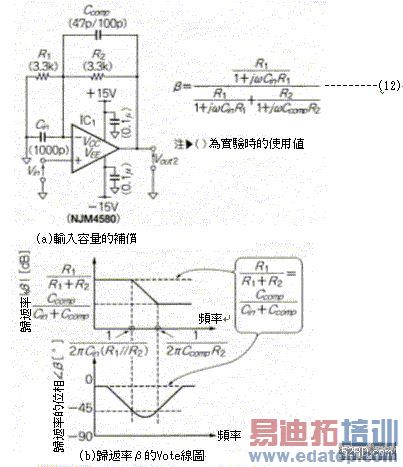
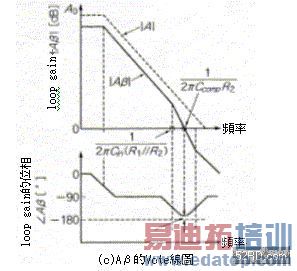 图8 输入容量的补偿方法与Loop Gain的频率特性 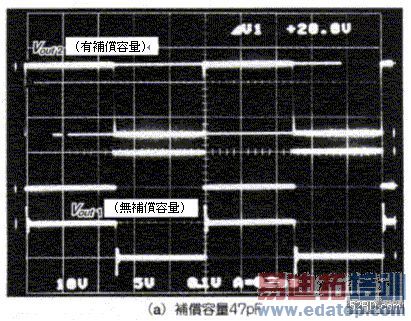
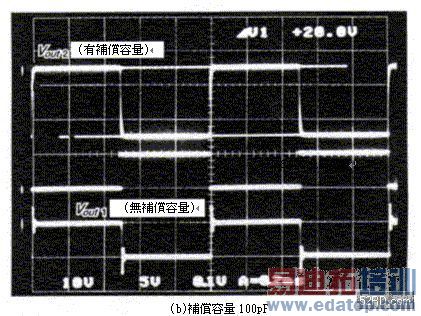 照片1 从step的反应观测输入容量的补偿效果
(0.2ms/div.,上方:5v/div 中间:1V/div., 下方:10V/div., )
(二).利用负载容量消除不稳定动作
‧追加设置电阻与电容作补偿
图9(a)是附加于OP增幅器的容量Cout造成的位相延迟典型范例;图9(c)则是追加设置电阻与电容作补偿的典型范例。
●利用模拟分析计算容量
图10(a)是将NJM072B当作OP增幅器,并加上图9(c)的定数模拟分析(simulation)构成的模拟分析用电路。根据NJM072B的资料表(data sheet)记载,图中的f0为16Hz,open loop gain为20万倍 ,等价输出阻抗为210Ω 。
根据图10(b)是频率特性分析结果可知,Cout=0.01µF,补偿容量Ccomp=200pF时,频率特性并未出现峰值(peak);图10(c)是step反应的分析结果,由图可知当Ccomp=300pF时,就不会再出现over shoot现象。
●未採用人工计算的理由
虽然市面上有许多有关OP增幅器方面的书籍,不过却很少介绍最佳补偿容量Ccomp计算方法,读者不妨计算图9(c)电路的传达关数,就可以发现它是由许多无意义,而且错综复杂的式子所构成,换句话说若是採用人工计算的话,势必耗费庞大作业时间,因此此处採用电脑模拟分析方式。不过必需提醒读者模拟分析只是佐证设计的工具,模拟分析本身并不具备电路设计功能。
●实验验证
接着使图9(c)的电路实际动作,藉此验证补偿效果。照片2是对电源施加0.1µF pass control,同时输入方形波时的波形。由图9(a)可知当补偿容量Ccomp=200pF时,会出现比模拟分析更大的over shoot,造成这种现象主要原因一般认为是图10的等价电路被大幅简化,而且实际上完全未考虑OP增幅器的寄生容量所致,因此当Ccomp=300pF时由于寄生容量已经补偿,所以不少出现over shoot现象。
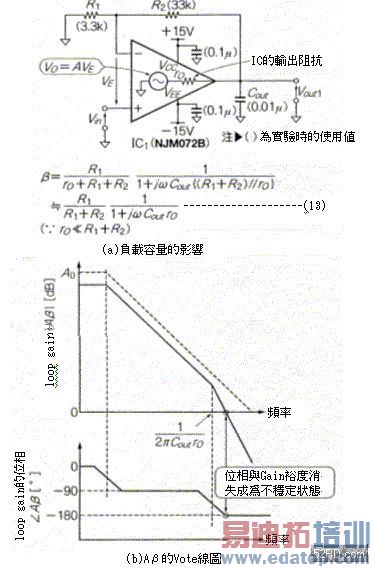 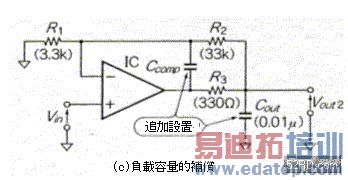 图9 负载容量的补偿与loop gain的频率特性 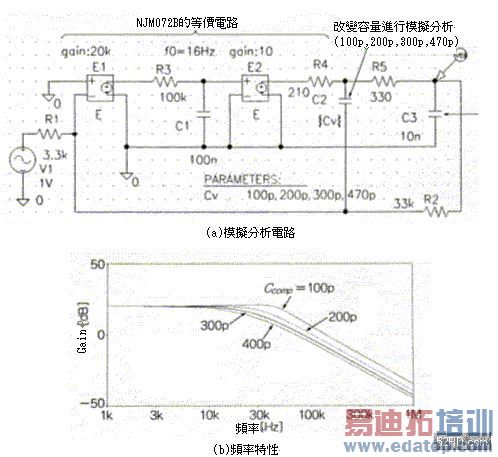 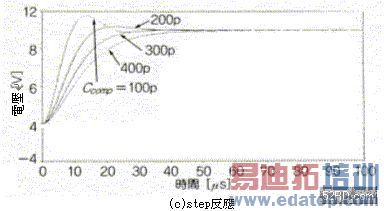 图10 模拟分析负载容量构成的补偿效果
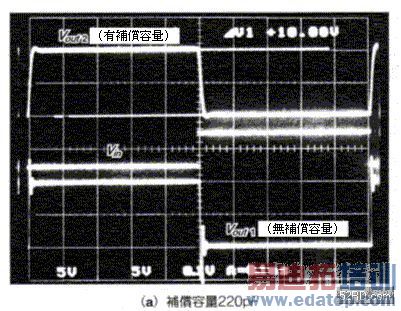 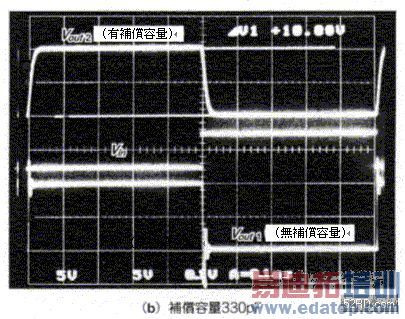
照片2 从step的反应观测输入容量的补偿效果
(0.2ms/div.,上方:5v/div 中间:1V/div., 下方:10V/div., )
| | |
如何支援微分电路
‧微分电路很容易发生波动
图11(a)是典型的微分电路。本电路设计上已经考虑波动问题,因此刻意使归返(return)电路具备OP增幅IC2特有的crossed loop gain G2一次延迟特性。本电路大量採用可变gain电路结构,例如图中的R3,R4都是可变电阻,因此gain的旋转角可作直线性变化。如果去除OP增幅IC2的话,本电路就变成T型归返电路,由于T型归返电路具有许缺点,所以一般会用OP增幅IC2加以消除。值得一提的是即使是差动增幅器的可变gain offset调整电路,也必需注意波动问题,此外图7(a)也是属于微分电路。
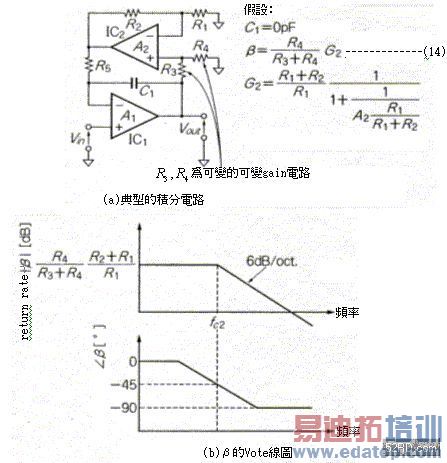
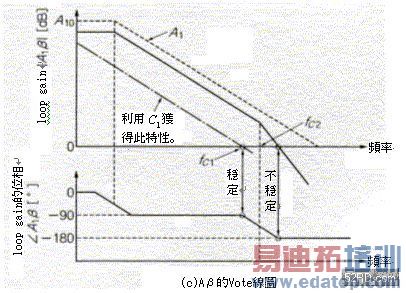
图11 可变gain电路的设计,结果变成微分电路的典型范例
‧如何对策抑制波动
图12(c)的实线是图11(a)的β,与图11(c)虚线的OP增幅器的open loop gain A1两者相乘的结果A1β,由图可知它属于二次延迟特性因此没有位相裕度,有鑑于此电路必需追加设置C1,同时降低OP增幅器IC1的实效性open loop gain A1,藉此使loop gain A1β变成图中1点锁线,如此就可以确保位相裕度,若以定量表示的话,下式就可以成立:
fc1<fc2
fc1是OP增幅器IC1的open loop gain变成1(0dB)时的频率;fc2是OP增幅器IC2的crossed loop gain变成-3dB时的频率。由此可知追加设置C1与R5,便可使归返率延迟的loop gain成为1,而更高的频率也能够发生反应,如此一来归返率的延迟在|A1β|=1时就不会有任何影响。
| | |
OP增幅以外的波动要因对策
‧追加emitter follower时必需设置电阻
根据以上的实验结果可知,只要设置电源pass control,由汎用OP增幅器构成的简易增幅电路,即使有微量的负载容量或是输入容量,电路也不会产生波动而且动作会非常稳定。然而实际上许多OP增幅器IC与电晶体或是FET的组合,却必需将OP增幅器IC以外的动态元件稳定度影响列入考虑,例如欲使输出电压变成±100V时,由于输出段的时定数非常接近OP增幅器IC的时定数,此时设计者必需绘制Vote线图进行检讨。
此外只想增加输出电流时,往往会将电路与连接emitter follower,此时必需注意emitter follower的时定数比OP增幅器IC小,虽然它对归返回路的稳定度几乎没有任何影响,不过base若未设置串联电阻的话,电路经常会产生波动,此外值得一提的是波动并不是归返loop产生波动,而是电晶体单体得寄生波动。
‧必需注意导线造成的位相旋转
随着增幅电路的频率范围改变,设计者必需将电路板组装时的导线影响也列入考虑。由于gain与频率特性并不是独立关系,因此若仔细观察gain的频率特性就可以了解位相的频率特性。如果是gain的话位相不会旋转;反之衰减倾度若是-6dB/oct时,位相会旋转成-900;若是-12dB/oct时,位相会旋转成-1800。
不过有些电路gain不会衰减,只有位相会旋转,这种电路属于传输线路的一种。它在低频时并不需要考虑信号的波长,不过当频率变高时就会出现影响。假设图12是无损失的传输线路,不过随着信号传输时间的增加,位相会开始回转。相当于一波长λ 的长度即使无衰减,位相也会回转3600;如果负归返loop的导线长度,是半波长λ /2的话,由于位相会回转1800,因此无法施加负归返。 位相的回转量在空气中大约是1.20/.MHz/m,换言之导线长度1m时,每1MHz位相会回转1.20;导线长度1m,频率为100MHz的话,位相会回转1200。如果有类似印刷电路板绝缘物时,由于诱电率的影响波长会缩短,因此位相的回转角度会更大,也就是说设计频宽超过数十MHZ的增幅电路时,必需将位相回转问题列入考虑。 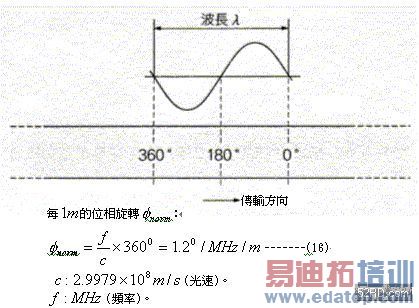
图12 频宽为数十MHz以上的增幅电路,必需考虑传输线路造成的位相旋转
|
|
上一篇:量测基础篇-DAQ基本要素与资料截取概念
下一篇:二极管的动作特性与应用





















