- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
量测基础篇-加速规原理
在开发感测器以用于测量加速度时,有几种实际的程序可供使用。在牵涉到飞行器(例如飞机和卫星)的应用中,加速规是以旋转质量(rotating mass)为基础,但是在工业界,最常见的设计是结合牛顿的质量加速定律和虎克的弹簧动作定律。本文将从弹簧质量系统、自然频率与阻尼、震动效果这几点切入,搭配范例介绍此原理。
弹簧质量系统
牛顿定律表示:如果一个质量m受到加速度a,那么必然有一个力量F作用于该质量上,可叙述为F = ma。虎克定律也指出,如果一个弹性常数为k的弹簧从它的平衡位置拉长(延伸)至Dx距离,那么必然有一个力量作用于弹簧上,表示为F = kDx。

图 5.23 基本的弹簧质量系统加速度规
在图5.23a中,我们看到一个质量,平放在基板上,没有滑动。这个质量用弹簧连接至基板,弹簧位于未延伸状态,未对质量施加力量。在图5.23b中,整个总成向左加速,如图所示。现在弹簧延伸,以提供将质量加速所需的力量。这种情形可以用牛顿定律和虎克定律的等式来加以描述:
ma = kDx (5.25)
其中 k = 弹簧常数(spring constant),N/m
Dx = 弹簧延伸,单位公尺(m)
m = 质量,单位公斤(kg)
a = 加速度,单位m/s2
等式 (5.25)将加速度的测量归纳为弹簧延伸量的度量(线性位移),因为:

如果加速作用的方向相反,同样的物理原则亦适用,只是弹簧是受到压缩,而非延长。等式 (5.26)仍然描述弹簧位移和加速度的关系。
弹簧质量原理适用于许多常见的加速规设计。将加速度转变为弹簧位移的质量称为试验质量(test mass)或振盪质量(seismic mass)。然后我们看到,加速度测量归纳为线性位移测量;大部份设计的差异处即在于如何进行这个位移测量。
自然频率和阻尼
仔细检视刚才描述的简单原则,就会发现弹簧质量系统的另外一项特性,使分析变得复杂。明确地说,一个包含弹簧和连接之质量的系统在某个特别的自然频率(natural frequency )下必然表现出摆动的现象。从之前的经验可知,如果我们将一个质量向后拉,然后放开它(在没有加速度的情况下)它会被弹簧拉回去,超过平衡点,然后来回摆盪。最后只有和质量和底座之间的摩擦力令该质量停止不动。一个位移测量系统会将这种摆盪现象视为实际发生了加速度。这个自然频率的计算方式为:

其中 fN = 自然频率,单位Hz
k = 弹簧常数,单位N/m
m = 振盪质量,单位kg
最后令质量停止的摩擦力由一个阻尼系数(damping coefficient)定义,它的单位是s-1。一般而言,摆盪的效果称为暂态响应(transient response),由一个週期性的阻尼讯号描述,如图5.24所示,其算式为:
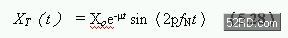
其中Xr(t) = 暂态质量位置
Xo = 巅峰位置,一开始
µ = 阻尼系数
fN =自然频率
等式(5.28)中的各项参数,自然频率,以及阻尼系数,对于加速规的应用有极大的影响。
震动效果
要描述自然频率和阻尼对于弹簧质量加速规的行为的影响,最好的方式是用施加振动的方式来形容。如果弹簧质量系统被振动的话,那么所造成的底座加速度可由等式 (5.23)得知:
a(t) = -w2xo sin wt
如果这应用在等式(5.25)中,我们可以知道质量运动是由下式提供:

其中所有的参数都已经说明过,而w = 2pf,使用/应用之频率。
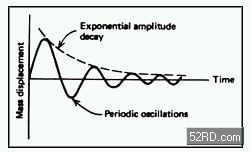
图5.24 A 受到推动刺激时,弹簧质量系统表现出自然摆盪现象。
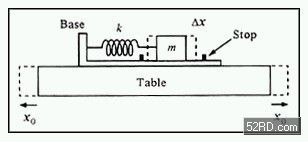
图5.25 A 弹簧质量加速规连接于一张桌子,这张桌子表现出振动的现象。桌子的运动极限是xo,质量运动为Dx。
为了说明等式(5.29)的预测,想像一下图5.25所呈现的状况。我们的模型弹簧质量加速度规是固定在一张振动中的桌子上。等式(5.29)中的xo是桌子振动的最大振幅,Dx 是加速规中的振盪质量的振动。因此,等式 (5.29)预测振盪质量振动峰值随着振动频率的平方而变动,但是与桌子振动振幅成线性关系。但是,这个结果并没有考虑到弹簧质量系统的自然振动。在将自然振动纳入考虑时,就会发生相当大的不同。
相关解决方案:
NI LabVIEW声音与振动工具组可以执行频率分析与频率反应
图5.26a显示实际的振盪质量振幅峰值与桌子振动频率的关系,再与预测中的简单频率平方做比较。你可以看到,当桌子频率等于加速规的自然频率时(也就是Dx的值经过峰值时),会出现一个共振效果。共振峰的振幅是由阻尼量来决定。振盪质量振动可由等式 (5.29)描述,最高约只能到达 fN/2.5。
图5.26b显示两个效果。第一个效果是实际的振盪质量运动受到加速器的实际大小限制。在共振时,它会击中总成内建的「停止」而限制其运动。这个图也显示出,对于远高于自然频率的频率而言,质量的运动与桌子运动峰值xo成正比,但是不与频率成正比。因此,它变成一个位移感测器。摘要而言:
1. f < fN – 就低于自然频率的施加频率而言,自然频率对于等式(5.25)和(5.29)所给予的基本弹簧质量响应的效果很小。最重要的原则指出,安全的施加频率上限是f < 1/2.5fN。
2. f > fN -就远比自然频率来得大的施加频率而言,加速规的输出值与施加频率无关。正如图5.26b所示,在这种情况下,加速规变成等式(5.20)的振动位移 xo 的测量。有趣的是,在这个例子里,振盪质量是静止的,而其外罩受振动驱使而绕着质量移动。一般性规则设定这个例子为f > 2.5 fN 。
一般来说,加速规不会使用在接近其自然频率的共振,因为输出值会呈现高度非线性状态。
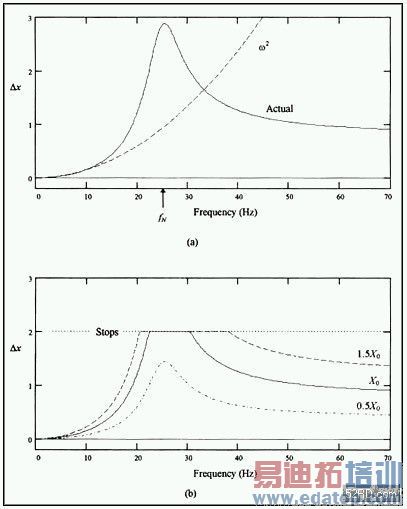
图5.26 在(a)中,弹簧质量系统对振动的实际反应与简单的w2 预测进行比较;
在(b)中,显示各种桌子运动峰值的效果
范例5.14
一具加速规具有振盪质量0.05 kg,弹簧常数为3.0 X 103 N/m。最大质量位移是±0 02 m(在质量到达停止点前)。试计算 (a) 可测量之最大加速度,单位g,以及(b)自然频率。
-解答-
当最大位移发生时,我们可以从等式(5.26)找到最大加速度。
a.

相关解决方案:
NI 4472动态信号撷取可同时将8条通道上的信号数字化,由DC转换为45kHz
或是因为

b.自然频率可由等式 (5.27)计算而得。

上一篇:HDTV带来高画质平面显示信号的量测挑战
下一篇:数字化电源的优势

