级联型逆变器相移PWM的相移量与输出谐波关系分析

摘要：阐述了相移PWM技术在级联型逆变器中的应用，并对相移PWM中各单体逆变器的相移与级联型逆变器输出频谱之间的关系进行了分析。当相移量为Ts/m时，输出谐波频率为原有的m倍。仿真和实验结果证实了分析的正确性。

关键词：级联型逆变器；多电平逆变器；相移

1    引言

    多电平逆变器由于可降低器件的开关应力，优化输出波形，提高转换效率等优点，目前在中大功率场合得到越来越广泛的应用。多电平逆变器目前主要包括二极管嵌位型、电容嵌位型、多单元级联型等^[1]。级联型逆变器将多个逆变单元串联起来，易于扩展，主要缺点是每个单元需要隔离的直流电源。为减少隔离电源数量，单元电路结构可以不完全相同。这种由不同单元串联而成的逆变器称为混联型逆变器。当电源电压不同时，可以增加输出电平种类^[2]。串联单元本身还可以是一个多电平逆变器，如二极管嵌位型逆变器^[3]。图1是一个由H逆变桥和五电平逆变器串联组成的混联型逆变器。级联型又可分为带隔离直流电源和带隔离输出变压器2种。分别如图2和图3所示。

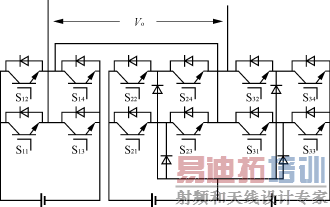
图1    混联型逆变器示例

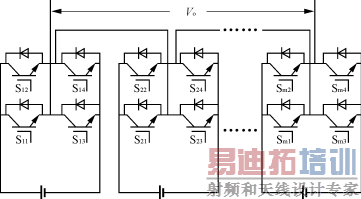
图2    带隔离直流电源的多重结构

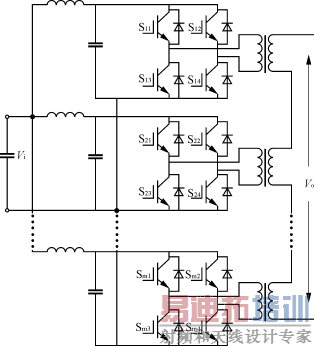
图3    带有输出隔离变压器的多重结构

    多电平逆变器输出正弦波的调制方法主要有2种，一种是基于基频的调制方法，使逆变器输出阶梯波逼近正弦波，可分为空间矢量控制和谐波选择消除，通过合适的选择阶梯波的时间和幅度，可有选择地减少或消除特定的开关谐波；另一种是基于高频的调制方法，通过高频调制，使得谐波频率更高，更易于滤除，可分为空间矢量调制和SPWM2种方式。

    多电平逆变器中随着级数的增加，空间矢量的个数呈几何次数增加，而数量较多的矢量可获得更好的控制效果。SPWM很易于从两电平方式扩展到多电平方式。多电平SPWM主要有多载波SPWM、相移SPWM和注入3次谐波提高母线电压利用率法。多载波SPWM将多个相邻三角波与正

    弦参考信号进行比较得到控制脉冲，适用于二极管嵌位和级联型逆变器。相移SPWM技术适用于级联型逆变器^[4][5][6]，通过将相位不同的载波信号与正弦参考信号比较得到触发脉冲。图4显示了一个三重级联型逆变器相移SPWM产生原理。相移SPWM可以提高输出波形中含有的谐波频率，从而使之更易于滤除。本文分析了各单体逆变器之间的相移与输出频谱之间的关系，并通过仿真和实验验证了分析结果。

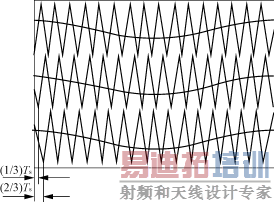
图4    三重级联型逆变器相移SPWM产生原理图  [p]

2    相移量与输出频谱之间的关系

    对于单体逆变器，其驱动信号产生原理与两电平SPWM逆变器完全相同。而对于不同的单体逆变器，输出的基波存在一个相位差。

    设逆变器由 m 个单体SPWM逆变器组成，第 i 个SPWM逆变器输出电压为 u _i，则串联输出总电压为

    u ₀= u _i（1）

    设单个逆变器输出单相双极性SPWM波，且波形正负半周期镜像对称，即

    u (ω t )=－ u (ω t +π)（2）

    为简化计算，设波形在正负周期内前后1/4周期以π/2为轴线对称，即

    u (ω t )= u (π－ω t )（3）

    则可用傅立叶级数表示为^[7]

    u (ω t )= a_n sin n ω t （4）

    设逆变器的一个开关周期为 T _s，各个逆变器输出时延为 T _s/ m ，则输出电压用傅立叶级数表示为

    u (ω t )= a_n sin（5）

由于

    sin=[sin n ωt cos( n ω )－sin( n ω )cos n ωt ]

        =sin n ωt cos( n ω )－cos n ωt sin( n ω )

        =sin n ωt cos( n 2π)－cos n ωt sin( n 2π)（6）

式中： T 为逆变器输出波形基波的周期，当基波为工频50Hz， T =20ms；

      T _s为开关周期，当开关频率 f _s为几十至几百kHz， T _s为几μs至几十μs。

    当 n =1时，可近似认为

    cos( n 2π)=m，

    sin( n 2π)=0（7）

    可见，串联后输出电压中基频成分为线性叠加。

    当 n =m时，有

    cos( n 2π)= m ，

    sin( n 2π)=0（8）

    可见，串联后输出电压中频率 f = mf _s的成分线性叠加。

    因此，我们可以得知， m 个输出依次时延 T _s/ m 的SPWM逆变器串联，其输出的基频成分幅值为线性叠加，输出含有 f = amf _s( a =1,2,...)的谐波，谐波的幅值亦为线性叠加。

    因此，若多重逆变器由 m 个单体逆变器组成，逆变器载波频率为 f _s，则第 i 个单体逆变器的时延为： [p]

    t =（9）

    可见，通过串联叠加，输出频谱中所含谐波成分更加高频化，可大大减小滤波电感的体积。

3    仿真与实验

3.1    基于MATLAB的仿真实验

    采用MATLAB对两个时延为 T _s/2的单相SPWM叠加得到双重SPWM波的情况进行仿真，条件为：开关频率 f _s=2.5kHz，调制比为0.8，时延 T _s/2。频域分析结果如图5所示。

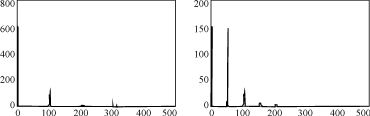
(a)    双重叠加输出电压的频谱分布    (b)    单个逆变器输出电压的频谱分布

图5    不同方式下输出电压的频谱分布

    可见叠加后的波形中开关谐波频率增加1倍，基频和谐波成份都得到叠加，证实了以上分析结果。

3.2    电路实验

    采用CM15-12H型的IGBT建立带高频输出变压器的单体全桥逆变器，逆变器为二重串联叠加结构，带小型滤波电感。控制方式采用相移PWM控制，采用ADSP2181为数字控制器，输出两路相互有时延的SPWM控制信号。输入电源由4节12V蓄电池串联提供，输出为220V，50Hz交流。

    当开关频率为12kHz，时延为 τ =42μs，负载为纯阻性，滤波输出波形如图6所示。波形的THD<3％。

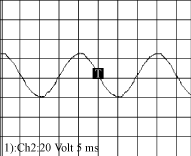
图6    实验的输出波形

4    结语

    本文对相移PWM的输出频谱进行了分析，得出了时延与输出频谱之间的关系。仿真与实验的结果证实了分析的正确性。