数字PID控制算法在温控系统中的应用

温度控制对于大型工业和日常生活等领域都具有广阔的应用前景。很多应用领域，需要精度较高的恒温控制，例如，根据外界变化，随时调节相应的LED亮度以达到所需色温值，可以实现更好的照明和装饰效果。在连续控制系统中，对象为一阶和二阶惯性环节或同时带有滞后时间不大的滞后环节时，PID控制是一种较好的控制方法。本文主要采用数字PID控制，通过单片机PID控制算法的程序实现。

1 数字式定时温控系统
    本文研制的数字式定时温控系统主要完成数据采集，温度、定时的显示，温度控制，温度定时的设定以及报警等功能。核心控制器由单片机完成，采用数字PID控制算法进行过程控制。加热器件选用热惯性小，温度控制精度高，速度快的电热膜，由单片机输出通断率控制信号进行控制。硬件框图如图1所示。

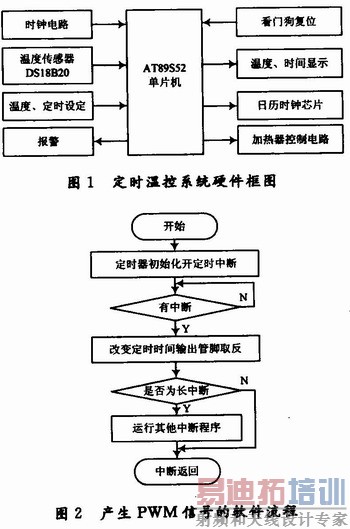
2 PWM功能的实现
    AT89S52内部有3个16位定时器：TO，T1，T2。用定时器T2实现PWM(脉宽调制)方式来对加热器件进行温度控制。设置T2CON中C／#T2=O(定时方式)，CP／#RL2=1且EXEN2=O时，T2是16位定时器。当计数溢出时，会设置T2CON中的TF2位，进而触发相关中断。用单片机系统实现，必须首先完成两个任务：首先是产生基本的PWM周期信号；其次是脉宽的调整，即单片机模拟PWM信号的输出，并且调整占空比。具体的设计原理：若想让它的负脉冲为2 ms，则正脉冲为20-2=18 ms，所以开始时在控制口发送低电平，然后设置定时器在2 ms后发生中断，中断发生后，在中断程序里将控制口改为高电平，并将中断时间改为18 ms，再过18 ms进入下一次定时中断，再将控制口改为低电平，并将定时器初值改为2 ms，等待下次中断到来，如此往复实现PWM信号输出。用修改定时器中断初值的方法巧妙形成了脉冲信号，调整时间段的宽度便可实现脉宽调整。实现其软件流程如图2所示。 [p]
    设n为定时器T2的初值，fi为单片机的系统时钟，本系统中fi=11．059 2 MHz定时方式下TL2寄存器每个机器周期(即12个晶振周期)增加1。这时PWM脉冲信号的“低”电平宽度为：
   
    通过改变定时器T2初值n，即可改变“低”电平的宽度tPWM-L，从而控制加热元件的加热时间，达到对温度进行控制的目的。当n=65 536时，P2．7引脚输出电平一直保持为“高”，加热元件一直处于断电状态；n=0时，P2．7引脚输出电平一直保持为“低”，加热元件一直处于通电加热状态。单片机根据从DSl8B20读取的温度值来确定n值，即确定加热元件的加热时间。

3 恒温控制算法
    PID基本算法是这样的：控制器的输出与控制器的输入(误差)成正比，与输入的积分成正比，与输入的微分成正比，为三个分量之和，其连续表达为：
   
    式中：TD为微分时间；e为测量值与给定值之间的偏差；Tl为积分时间；Kp为调节器的放大系数。
    对式(2)两边进行拉氏变换，可以得到PID调节器的传递函数为：
   
    采用不同的方法对式(3)的D(s)离散化，就可以得到数字PID控制器的不同算法。用矩形法数值积分代替式(3)中的积分项，对导数用后向差分逼近，得到：
   
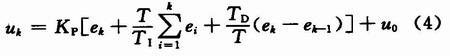
    式中：uo是由式(2)中的不定积分变为式(4)中的定积分所具有的积分常数；T为采样周期。式(4)就是数字PID控制器位置式算法的表达式，其输出控制量uk对应于系统的输出(位置)是全量输出。
    由式(4)可推算出控制量的增量为：
   
    式(5)就是数字PID控制器增量式算法的表达式，其输出为系统的△uk。
    采用增量式算法，系统中需增加一个积分装置，但在本恒温系统中，控制对象本身就具有积分作用，因此无需加积分装置。
    与位置式算法相比，在增量式算法中，计算误差对控制量影响小。这是因为位置式算法控制器输出的是全量，每次输出均与过去的所有状态有关。计算机的位数是有限的，当累加结果产生上溢出时，丢失一部分控制量；当采样周期短，误差很小时，计算机认为是零，不进行累加，这两种情况均会产生累加误差。而增量式算法在计算△uk时只用到最近的三次采样值，以前的状态不影响本次输出。
    为简化计算机的运算，把式(5)改为下面的形式：
   
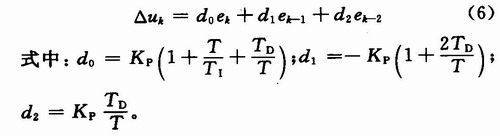
    可以根据式(6)编写程序，由计算机实现。Kp，TD，TI，T由参数整定确定。对于简单系统，可以采用理论计算的方法确定这些参数，但是稍微复杂一些的系统，采用理论计算的方法就困难了。因此几乎都是用工程的方法对参数进行整定。调节器参数的整定是一项繁琐而又费时的工作，因此，近年来国内外在数字PID调节器参数的工程整定方面做了大量的研究工作，归一参数的整定法是一种简易的整定法。
    根据大量实际经验的总结，人为设定约束条件，以减少独立变量的个数，例如取：
   
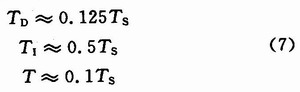
    式中：Ts是纯比例控制式的临界振荡周期。
    将式(7)代入式(6)中，可得数字PID控制器的差分方程为：
   
    对比式(6)和式(8)可知，对4个参数的整定简化成了对一个参数Kp的整定，使问题明显地简化了。
    采样周期T的取值，从数字PID控制器对连续PID控制器的模拟精度考虑，采样周期越小越好，但采样周期小，控制器占用计算机的时间就长，增加了系统的成本。因此采样周期的选择应综合考虑各方面因素，选取最优值。
    在恒温控制系统中，控制输出为定时器T2初值n(O≤n≤65 536)，误差为温度设定值Tset与DSl8B20检测值之差Tread。因为电阻丝的功率是有限的，初始温度低于温度设定值Tset较大时，可以不用数字PID控制。可以根据电阻丝的功率设定一个误差值emax，当e>emax时，一直加热，输出n=O；当e<0时，停止加热，输出为n=65 536。只有当O≤e≤emax时，才用数字PID控制。
    为保证温度控制的实时性，根据文献，温度控制程序采用定时中断方式，定时长为采样周期T，且中断优先级设得比其他中断高，用增量式算法其程序流程图如图3所示。 [p]

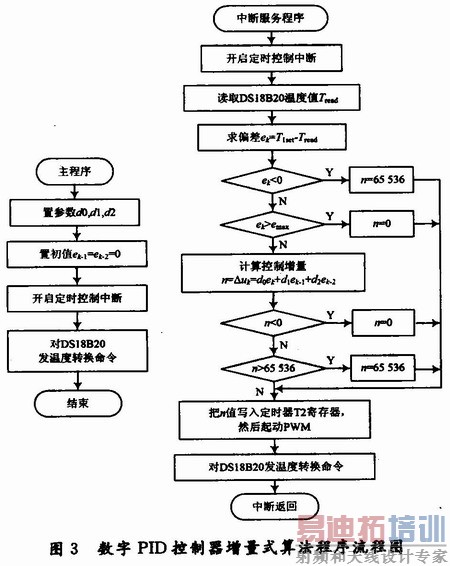
4 恒温控制结果
    根据温度控制精度和采样时间的要求，本设计对DSl8B20的温度转换结果选择12位，采样周期定为T=O．408 s。当加热元件功率选用100 W，温度设定值Tset=30℃时，用归一参数法整定数字PID控制器的参数，当参数Kp=150时，得到数字PID控制曲线如图4所示。

5 结语
    在介绍利用AT89S52单片机实现PWM功能的基础上，讨论了数字PID控制算法对恒温控制的应用。从控制结果来看，这种控制方法可以得到较理想的控制效果，温度波动均可控制在±O．125℃之内。该技术已应用于定时控温发酵器、保健垫等产品中，运行良好，获得了良好的社会效益和经济效益。现正在尝试用于无影照明系统的色温控制，实现更好的无影照明效果。