自适应滤波算法的仿真及工程实现

0 引 言
    自适应滤波理论是20世纪50年代末开始发展起来的。它是现代信号处理技术的重要组成部分，对复杂信号的处理具有独特的功能。自适应滤波器在信号处理中属于随机信号处理的范畴。对于随机数字信号的滤波处理，通常有维纳(Weiner)滤波器、卡尔曼(Kal-man)滤波器和自适应(Adaptive)滤波器。维纳滤波器的权系数是固定的，适用于平稳随机信号；卡尔曼滤波器的权系数是可变的，适用于非平稳随机信号。但是，只有在对信号和噪声的统计特性先验已知的情况下，这两种滤波器才能获得最优滤波。但在实际应用中，常无法确定这些统计特性的先验知识，或统计特性是随时间变化的，因此，在许多情况下，维纳滤波器或卡尔曼滤波器实现不了最优滤波，而自适应滤波不要求已知信号和噪声的统计特性，因而可以提供理想的滤波性能。当前，自适应滤波技术已广泛应用于自适应噪声对消、语音编码、自适应网络均衡器、雷达动目标显示、机载雷达杂波抑制、自适应天线旁瓣对消等众多领域。
    在一些信号和噪声特性无法预知或它们是随时间变化的情况下，自适应滤波器通过自适应滤波算法调整滤波器系数，使得滤波器的特性随信号和噪声的变化而变化，以达到最优滤波的效果。这里在对自适应滤波算法研究的基础上，给出了不同信噪比情况下，LMS算法的仿真实现及基于DSP的工程实现，并对两种实现方法的结果进行了验证、分析比较。

1 自适应滤波理论
    所谓自适应滤波，就是利用前一时刻已获得的滤波器参数等结果，自动调节现时刻的滤波器参数，以适应信号和噪声未知或随时间变化的统计特性，从而实现最优滤波。自适应滤波器由两个部分组成：一是滤波器的结构；二是调节滤波器系数的自适应算法。自适应滤波器的特点是自动调节自身的冲激响应，达到最优滤波，此算法适用于平稳和非平稳随机信号，并且不要求知道信号和噪声的统计特性。
1．1 自适应滤波器结构
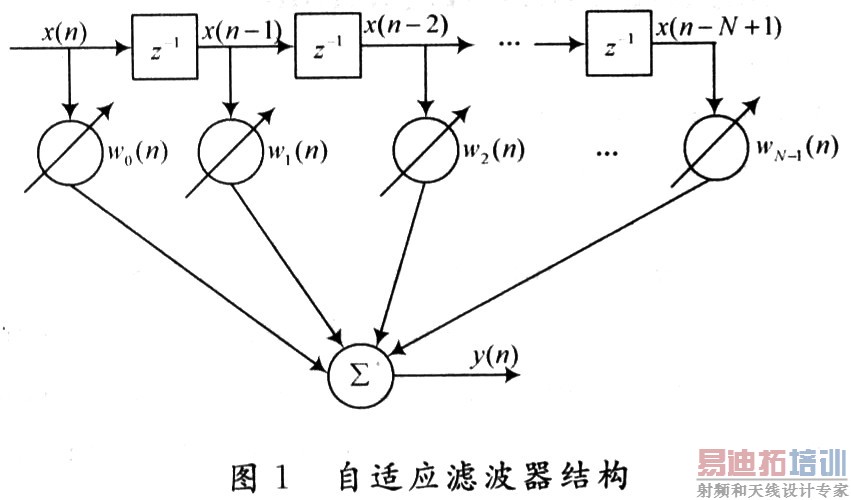
    自适应滤波器主要有无限冲激响应(IIR)和有限冲激响应(FIR)两种类型。滤波器结构的选择对算法的处理起着重要的影响；IIR型结构滤波器的传输函数既有零点又有极点，它可以用不高的阶数实现具有陡峭通带特性，缺点是稳定性不好，且相位特性难于控制。FIR滤波器是全零点滤波器，它是稳定的，且能实现线性的相位特性，因此，自适应滤波器的结构通常采用F1R型滤波器的横向结构，结构如图1所示。
   
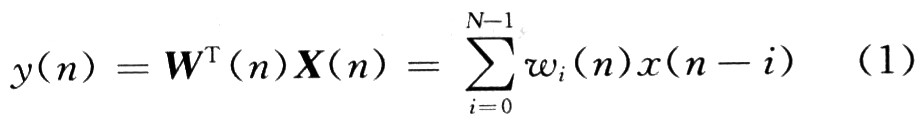
式中：n为时间序列；N为滤波器阶数；x(n)=[x(n)，x(n-1)，…，x(n-N+1)]T为输入矢量；W(n)=[ω0(n)，ω1(n)，…，ωN-1(n)]T为权系数矢量。

1．2 LMS自适应滤波算法
    LMS自适应滤波算法是根据最小均方误差准则进行设计的，LMS算法的目的是通过调整系数，使输出误差序列的均方值最小化，并且根据这个数据来修改权系数。误差序列的均方值ε表示为：
   
式中：d(n)为理想信号；e(n)为输出误差序列。将式(1)中的y(n)代人式(2)中有：
   
式中：R=E[X(n)XT(n)]为N×N自相关矩阵，表示输入信号采样值间的相关性矩阵。P=E[d(n)X(n)]为N×1互相关矩阵，表示理想信号d(n)与输入信号矢量的相关性。
    在均方误差最小时，最佳权系数应满足如下方程：

   
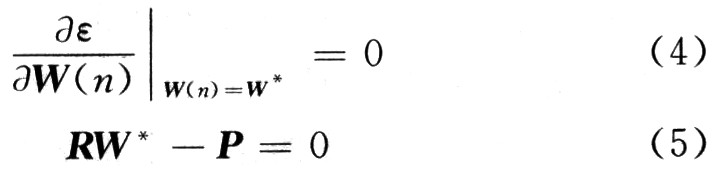
即：
    这是一个线性方程组，如果R矩阵为满秩矩阵，则有R-1存在，可得到权系数的最佳值满足：
   
    由式(6)可以知道，求出R和P就可以得到W*。由前几式可知，R是X(n)的自相关矩阵，P是d(n)与 X(n)的互相关矢量。
    LMS算法是以最陡下降法为原则的迭代算法，即W(n+1)矢量是W(n)矢量按均方误差性能平面的复斜率大小调节响应一个增量，即：
   
式中：u表示自适应步长；(n)为n次迭代的梯度，表示为：
   
    由式(7)产生了求解最佳权系数W*方法的两种方法，一种是最陡梯度法，其基本思路为：设定初始权系数W(0)，用式(7)迭代公式计算，迭代直到W(n+1)与 W(n)误差小于规定范围。其中(n)的E[]计算可用下面的估计值表达式来计算：
   
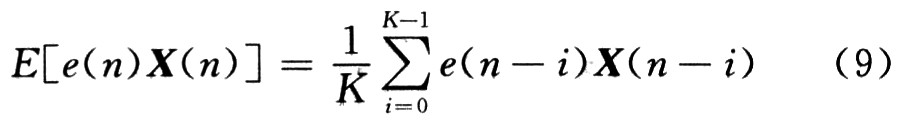
式中K取值应足够大。如果用瞬时-2e(n)X(n)来代替上面对-2E[e(n)X(n)]的估计运算，就产生另一种算法：随机梯度法，即Widrow-Hoff的LMS算法。迭代公式表示为：
   

[p]
2 仿真及工程实现
2．1 LMS算法的仿真实现
    假定输入信号由正弦波信号和高斯白噪声组成。其中正弦波信号的频率f0=1 000 Hz，幅度A=2，FIR滤波器的阶数N为128；当白噪声的均值为0，其方差δ分别为0．64，2，6．32，即信噪比(SNR)分别为5 dB，0 dB，-5 dB时，采用LMS算法进行滤波的结果分别如图2～图4所示。

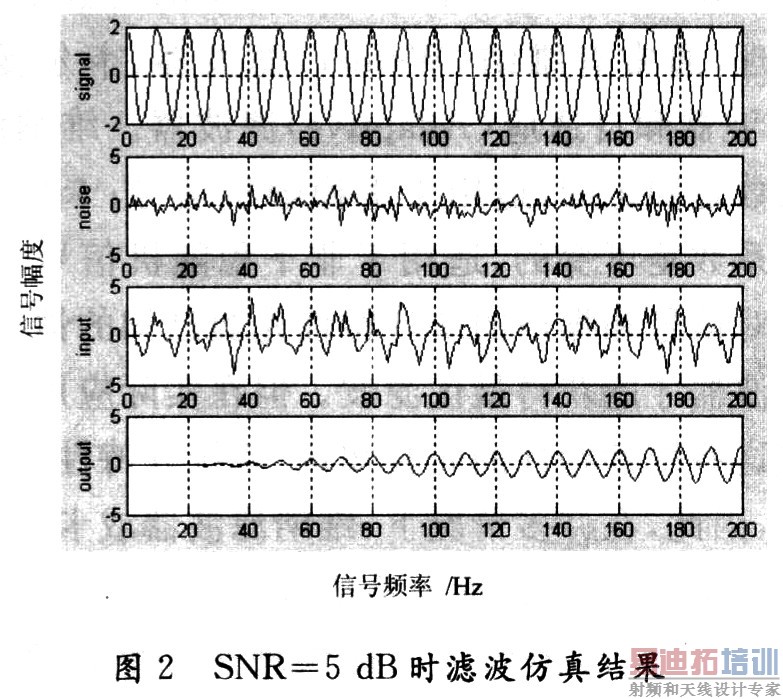
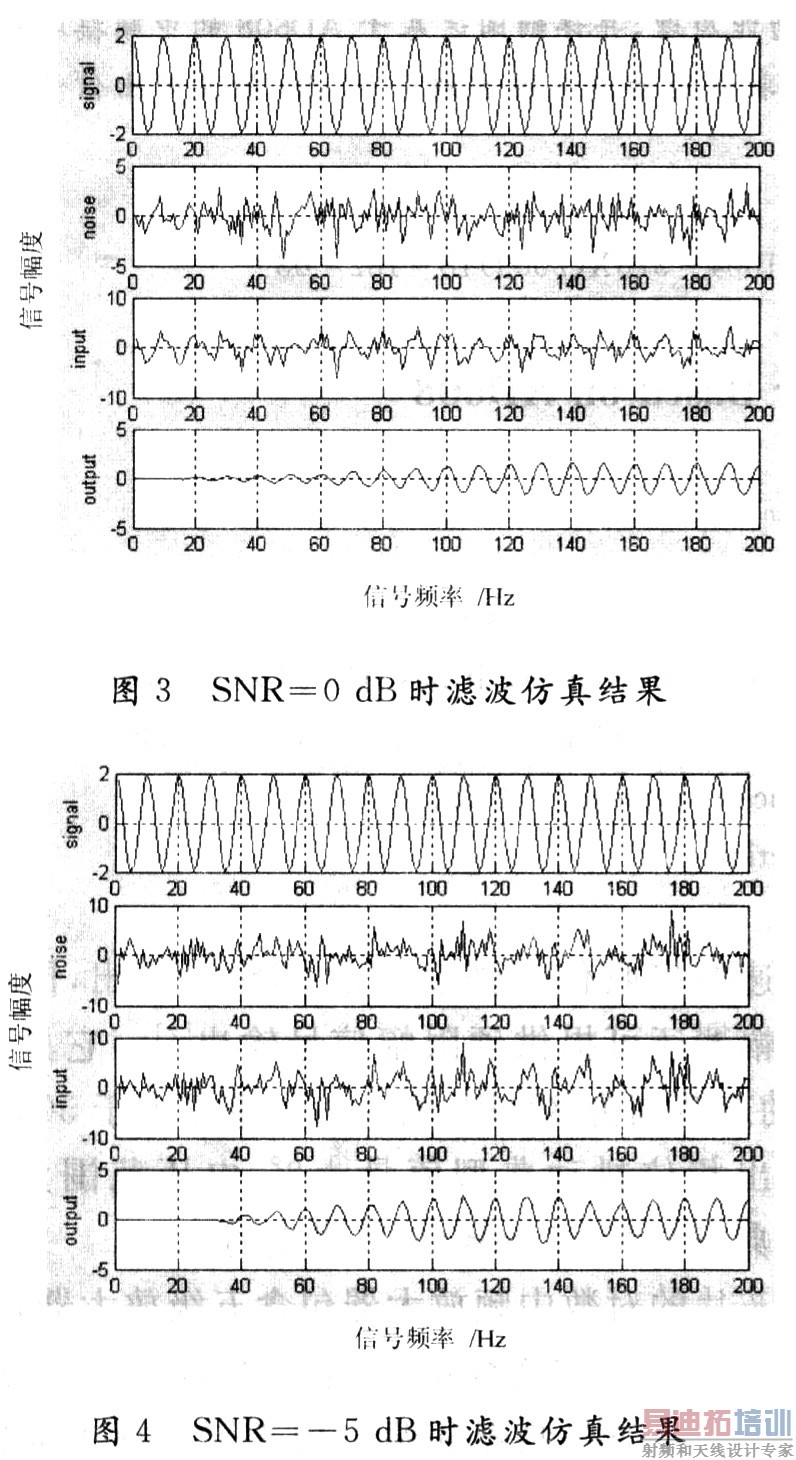
2．2 LMS算法的DSP实现
    设定采样数据的点数为1 024点，滤波器的全系数设定为128阶，自适应步长为5×10-5。设定输入信号为正弦波+噪声信号，其中正弦波的周期T=256 s，幅度A=200，正弦波信号功率Ps=20 000；噪声设定为零均值，方差δ分别为2 000，6 330，20 000，相应的信噪比 SNR=10 dB，5 dB，0 dB，根据自适应迭代公式(8)，使用DSP编程实现自适应滤波算法，由DSP的CCS开发环境图形分析工具得到测试结果如图5～图7所示。

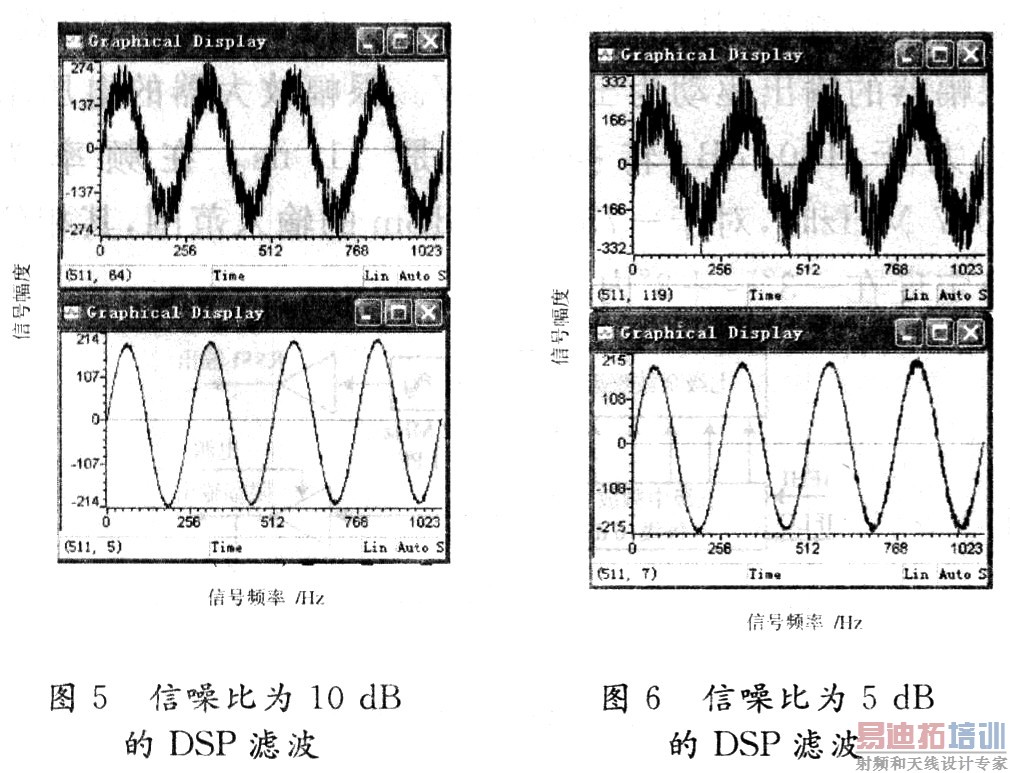
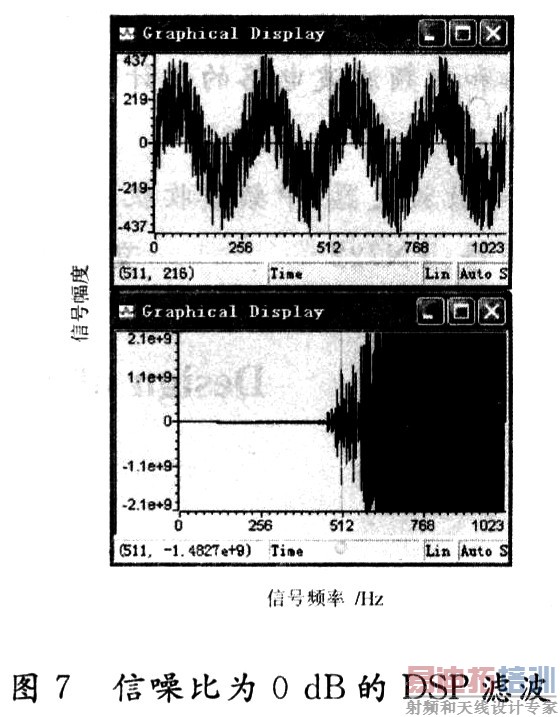
    根据图7比较分析可以得出：
    (1)无论是使用Matlab仿真方法还是使用DSP方法实现LMS算法，随着信噪比的降低，自适应滤波效果减弱。
    (2)在信噪比位于0 dB之上时，两种方法都可以取得较好的滤波效果。
    (3)在信噪比位于0 dB(或0 dB以下)，仿真方法可以取得较好的滤波效果，但工程上却不能实现，即当信噪比位于0 dB时，LMS算法已失去工程上的应用价值。

3 结 语
    这里在对自适应滤波理论研究的基础上，对LMS自适应滤波算法进行了研究，给出了不同信噪比条件下，LMS算法的仿真实现及基于DSP的工程实现，并对两种实现结果进行了分析比较，通过如图7所示，LMS算法在信噪比较高时，除噪效果非常显著，当信噪比较低的时候，仿真上可以得到的比较理想的滤波效果，工程上却无法实现。该结论对于指导自适应滤波理论的工程实践具有指导作用。