- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
抑制SSN的新型内插L-EBG结构
摘要:本文提出的是一种基于平面型EBG (Electromagnetic Bandgap)结构的创新型结构,对于同步开关噪声(Simultaneous Switching Noise, SSN)的抑制有更优秀的特性。我们设计的这款新型EBG结构,是在周期性L-bridge EBG结构的基础上,在一些单元内插小型的L-bridge EBG。通过仿真验证,此结构具有传统型L-bridge EBG结构所不具有的超带宽抑制能力和较大的抑制深度。然后我们运用电路模型和平行板谐振腔原理分析了该结构上下变频。另外,通过3-D仿真,得到结构的IR-Drop和直流阻抗。最后,通过眼图验证该结构的信号传输特性。
引言
近年来,随着电子系统的工作频率越来越高,边沿速率越来越快,供电电压越来越低[1],造成电压噪声容限下降,使得SSN已成为高速数字电路设计的难点之一。由于SSN会造成严重的信号完整性或电源完整性问题,为了保证系统正常工作,对SSN的抑制尤为重要[2-3]。
EBG结构是有效抑制SSN的方法之一。目前,已经发展出多种EBG结构,例如以蘑菇型EBG(Mushroom-type EBG)结构为代表的3D 嵌入式EBG结构[4-8]和以L-Bridge EBG结构为代表的共面型EBG(Coplanar compact EBG)结构[2,9-13]。
本文提出了一种新型L-bridge EBG结构。该结构每个单元的电源平面插入小型的L-EBG,地平面保持完整。并通过仿真,在抑制深度为-30dB时,带宽从461 MHz一直延伸到12GHz。
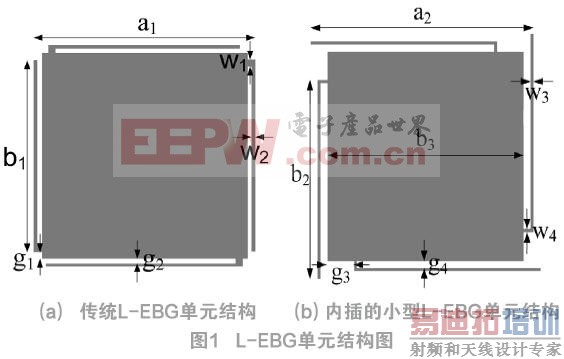
1 新型内插L-EBG结构方法的分析设计
新结构是在3×3单元组成的90×90×0.4mm3周期性L-Bridge EBG结构基础上,有选择性地在原单元中心区域挖空并插入小型L-Bridge EBG结构。其中L-Bridge单元结构如图1(a),内插的L-Bridge单元结构如图1(b)所示。此结构仅在电源平面进行开槽,地平面则保持完整。具体参数如下所示:a1=30mm,a2=15.9mm,b1=28.2mm,b2=14.3mm,b3=14mm,g1=0.3mm,g2=0.5mm,g3=0.9mm,g4=0.5mm,w1=0.2mm,w2=0.1mm,w3=0.2mm,w4=0.2 mm。介质为介电常数εr=4.4,耗散因子为tanδ=0.02的FR4材料。介质厚度为0.4mm,铜箔厚度为0.035mm。如图2所示,为验证此结构对于SSN噪声的抑制能力,共设定4个50Ω的集总同轴端口,各个端口的物理位置为:(30mm,30mm,0mm),(0mm,60mm,0mm),(-30mm,30 mm,0mm)和 (-30mm,0mm, 0mm),其中将Port1设为输入端口,剩余端口均设定为输出端口。
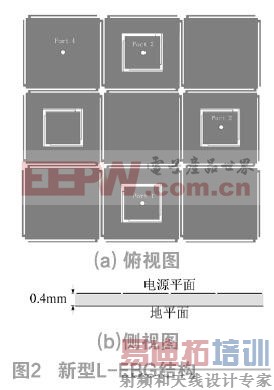
为得到所提出结构的电源噪声抑制能力,通过Ansoft HFSS 15软件对此结构进行了电磁仿真,最终得到所需端口间的S参数的幅值,如图3所示。从图3可以看出,在-30 dB抑制深度下,新型选择性内插式EBG结构的噪声抑制效果良好,阻带从461 MHz左右延伸到12 GHz并覆盖所有所设端口,具有超带宽抑制能力。
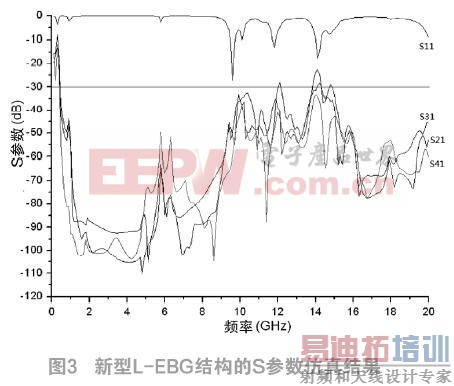
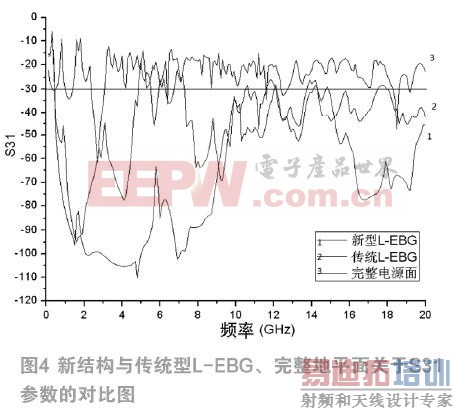
图4所示为新型L-EBG与传统的L-bridge EBG结构(没有内插的L-EBG结构,其他尺寸保持相同)、完整地平面的电源噪声抑制能力的对比。不难看出,在-30dB为参考标准的抑制深度下,提出的结构与传统的L-EBG结构下截止频率大致相同,但是很显然新结构的上截止频率相比于开槽型L-bridge EBG结构要大很多,增加了近7.2GHz。可见新提出的EBG结构具有较大的带宽优势。
2 上下边频估算
2.1 下边频估算
共面型EBG结构的下边频一般在几百兆频带内,而EBG结构单元的周期长度一般仅为数十毫米。EBG结构工作在这频率段内时,其几何长度与工作波长相比可忽略不计。因此在低频段,EBG结构在功能上等同于由多个集总电路元件组成的低通滤波器。这些元件由EBG单元的总体尺寸决定。这些集总元件包括平面电容Cp及宽导体方形平面回路电感Lp,桥连线电容Cb、电感Lb以及单元块间隙耦合电容Cg。这些参数的表达公式分别如下[14-15]:
![]() (1)
(1)
![]() (2)
(2)
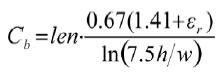 (3)
(3)
![]() (4)
(4)
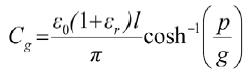 (5)
(5)
本文来源于中国科技核心期刊《电子产品世界》2016年第6期第52页,欢迎您写论文时引用,并注明出处。
[p]式中ε0、μ0分别为自由空间的介电常数和磁导率,εr为相对介电常数,S为平板正对面积,h为电源地平面介质厚度,len为传输线线长,w为传输线线宽,k为常数0.2nH/mm,l为EBG单元块方块边长,p为EBG单元块周期长度,g为相邻单元块间隙。
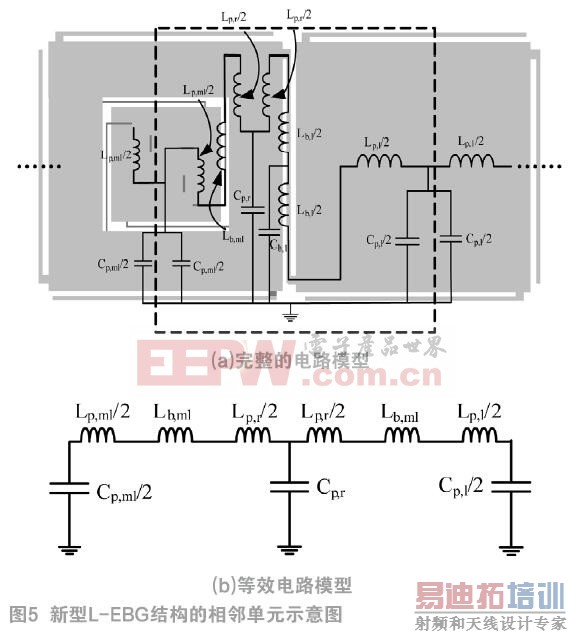
图5(a)中所标注的虚线框内是新提出的L-EBG内插L-EBG结构的任意两个相邻单元的等效电路模型[16]。为了简化分析,分三部分介绍该等效模型:第一部分,Cp,l和Lp,l分别为未内插L-EBG的电源层和地平面间等效电容和等效电感;第二部分,Lb,l和Cb,l分别为连接桥对地的等效电感和等效电容;第三部分,Cp,ml、Lp,ml和Lb,ml分别为内插单元结构的对地等效电容、回路电感和桥连电感,Cp,r和Lp,r分别是1/4正方环平板电容和回路电感。
由于Cb,l较大,可近似看成开路,等效时可以忽略,得到简化等效电路模型如图5(b)所示。易知该电路有两个并联谐振回路,其谐振点分别如下所示:
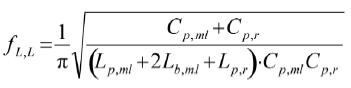 (6)
(6)
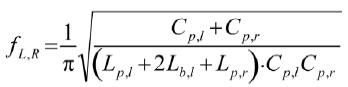 (7)
(7)
所以新结构有两个谐振频率点,我们可以得到该结构的下截止频率:
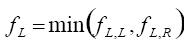 (8)
(8)
其中min( )为取最小值函数。
根据式(6)~(8)可以计算出fL,L=492 MHz,fL,R=434MHz,与实际仿真相差近80MHz,原因在于公式的估算以及电容电阻的忽略,在可接受范围内。
2.2 上边频估算
当截止频率到几GHz甚至几十GHz的时候,电磁波的工作波长与结构单元的尺度相当,所以不能使用上述的集总参数电路模型来计算上截止频率。本章节采用的是平行板谐振腔理论[17-19]来计算新结构的上截止频率fH,即单元结构中电源层与其正对面的地平面构成的谐振腔所产生的谐振主模频率。可以用式(9)来计算[17]:
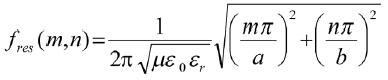 (9)
(9)
这里,fres(m,n)为平面谐振的频率,μ为自由空间导磁率,ε0为自由空间介电常数,εr为介质相对介电常数,a和b是金属平面的长和宽,m和n为长度和宽度方向上的谐振模式。在接近主模谐振频率时,发生的噪声耦合现象最为显著,因此,只需要关注主模频率,其表达式为:
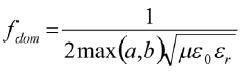 (10)
(10)
不同于下截止频率,新结构的上截止频率为谐振腔主模频率中的最大者,新型L-EBG结构的主模频率为:
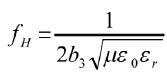 (11)
(11)
经计算,fH=10.71GHz,与仿真的12 GHz有一定的误差,但是如果选取-35dB为抑制深度,仿真的结果为10 GHz,原因在于计算-30dB与-35dB已无任何区别。
2.3 直流压降
直流压降(IR-DROP)即为直流电流流过一个导体时所产生的电压差。由于PDN阻抗的存在,使得电源的输出电压与芯片电源引脚之间存在电压差。本文提出的新型内插L-EBG结构较为复杂,当我们研究EBG结构抑制同步开关噪声的时候,IR-DROP是一个不得不考虑的问题。本文使用CST EM Studio分析新提出结构的IR-DROP。
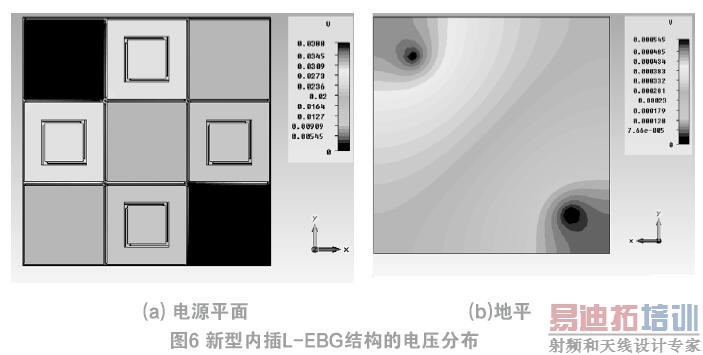
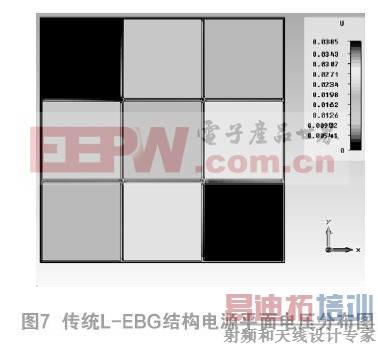
在CST中导入新结构的仿真模型,在电源平面的两个最远端口处添加辅助的理想电导体,因为距离最远,产生的压降最大,其中一端口加上1 A的直流电流激励,便可以看到电压在电源平面的分布情况。按照类似的方法,在地平面观察地平面的电压分布。仿真结果如图6所示,新结构的电源平面压降、地平面压降的最差情况分别为38.8 mV和0.545 mV,提供的直流电流为1 A,易得电源地平面阻抗,地平面阻抗分别为38.8 mΩ和0.545 mΩ。为了与传统L-EBG结构相对于,图7所示为传统的L-EBG结构电源平面电压分布图,易知其直流阻抗为38.5 mΩ,新结构增加了0.3 mΩ的阻抗,这是由于内插L-EBG的桥连线长度的增加,使得阻抗增加,但是增加的直流阻抗完全在可接受范围之内。
3 新结构的信号完整性分析
虽然本文所提出的选择性内插式EBG结构具有上述所提的超带宽SSN抑制特性,但是我们不得不承认如果传输线以刻蚀的电源平面为参考信号,相当于破坏了传输的返回路径。因此,对新结构的信号传输特性进行分析是非常有必要的。
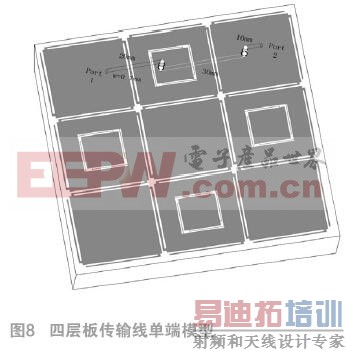
如图8所示,我们考虑一条长度为60 mm的传输线。此信号线通过两个过孔经由第一层传输到第四层并再次回到第一层。PCB的第二层和第三层分别为图形化电源平面和完整地平面,且相邻两层间的介质厚度为0.4 mm。Port 1、Port 2位于信号线的两端。
不返回零值(NRZ)的28-1伪随机序列(PRBs)作为端口1的激励,在端口2处监测信号的传输特性。发送的PRBs速率为2.6 Gb/s,摆幅0.5 V,125 ps的边沿速率。通过Ansoft Designer V4.0仿真,得到了传统L-EBG结构和所提结构的眼图,如图9所示。
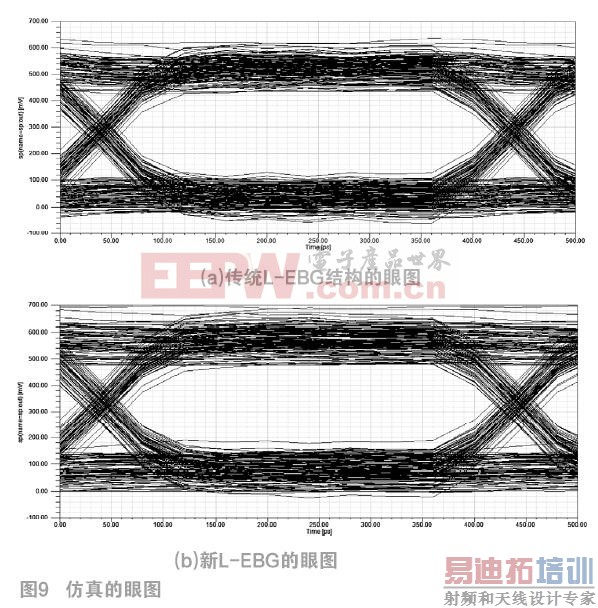
眼图的质量主要由最大眼高(MEO)和最大眼宽(MEW)两个参数决定。其中眼高指示电压噪声,而眼宽指示时序抖动。参考板的眼高为342mV,眼宽362 ps;新型EBG板的眼高为325 mV,眼宽为336 ps。可见所提出结构在接收信号的信号质量上相对传统型的L-EBG几乎没啥影响。
4 总结
本文提出了一种基于周期性共面EBG结构的选择性内插方法以增强对SSN噪声的抑制能力。相比于传统的L-bridge EBG,基于此方法设计的结构在阻带带宽和抑制深度上都有较大提高。同时,我们通过对该结构建立电路和谐振腔模型分别分析了所设计结构的上下截止频率,并分析了它的IR-Drop和直流阻抗。最后我们验证了该结构对信号传输的影响。
参考文献:
[1] H-R. Zhu, J-F. Mao, “Localized Planar EBG Structure of CSRR for Ultrawideband SSN Mitigation and Signal Integrity Improvement in Mixed-Signal Systems,” IEEE Trans. Compon., Packag., Manuf. Technol., vol. 3, no. 12, pp. 2092-2011, Dec . 2013.
[2]. Saketh Manukonda, K.Sridhar, and Samundiswary P, “UWB suppression of simultaneous switching noise using multi-slit L-bridge EBG structure,” International conference on Communication and Signal Processing, April. 2013, pp.447–450.
[3]. T. H. Ding and Y. S. Li, “Efficient method for modeling of SSN using time-domain impedance function and noise suppression analysis,” IEEE Trans. Compon. Packag., Manuf. Technol., vol. 2, no. 3, pp. 510-520, Mar. 2012.
[4]. L Li, B Li, H-X Liu, and C-H Liang, “Locally resonant cavity cell model for electromagnetic band gap structures,” IEEE Trans. Antennas Propag., vol. 54, no. 1, pp. 90-100, Jan. 2006.
[5]. J. Li, J. Mao, and M. Tang, “Mushroom-type ground plane structure for wideband SSN suppression in high-speed circuits,” IEEE. Microw. Wireless Compon. Lett., vol. 21, no.12, pp. 646-648, Dec. 2011.
[6]. C-D. Wang, and T-L. Wu. “Model and mechanism of miniaturized and stopband-enhanced interleaved EBG structure for power/ground noise suppression,” IEEE Trans. Electromagn. Compat., vol. 55, no. 1, pp. 159-167, Feb. 2013.
[7]. L. Peng, C-L. Ruan, and Z-Q. Li, “A novel compact and polarization-dependent mushroom-type EBG using CSRR for dual/triple-band applications,” IEEE. Microw. Wireless Compon. Lett., vol. 20, no. 9, pp. 489-491, Sep. 2010.
[8]. M. Kim, K. Koo, C. Hwang, Y. Shim, J. Kim, and J. Kim, “A compact and wideband electromagnetic bandgap structure using a defected ground structure for power/ground noise suppression in multilayer packages and PCBs,” IEEE Trans. Electromagn. Compat., vol. 54, no. 3, pp. 689-695, Jun. 2012.
[9]. P. H. Rao, and M. Swaminathan, “A novel compact electromagnetic bandgap structure in power plane for wideband noise suppression and low radiation,” IEEE Trans. Electromagn. Compat., vol. 53, no. 4, pp. 996-1004, Nov. 2011.
[10]. T-L. Wu, C-C. Wang, Y-H. Lin, T-K. Wang, and George Chang, “A novel power plane with super-wideband elimination of ground bounce noise on high speed circuits,” IEEE Microw.Wireless Compon. Lett., vol. 15, no. 3, pp. 174-176, Mar. 2005.
[11]. Y. Shi, W. Tang, S. Liu, X. Rao, and Y. L. Chow, “Ultra-wideband suppression of power/ground noise in high-speed circuits using a novel electromagnetic bandgap power plane,” IEEE Trans. Compon. Packag., Manuf. Technol., vol. 3, no. 4, pp. 653-660, Apr. 2013.
[12]. J. Qin, O. M. Ramahi, and V. Granatstein. “Novel planar electromagnetic bandgap structures for mitigation of switching noise and EMI reduction in high-speed circuits,” IEEE Trans. Electromagn. Compat., vol. 49, no. 3, pp. 661-669, Aug. 2007.
[13]. L. Li, Q. Chen , Q. Yuan, and K. Sawaya, “Ultrawideband suppression of ground bounce noise in multilayer PCB using locally embedded planar electromagnetic band-gap structures,” IEEE Antennas Wireless Propag. Lett., vol. 8, pp. 740-743, 2009.
[14] E. Bogatin, Signal and Power Integrity - Simplified, 2nd ed. NJ: Pretince Hall, 2009.
[15] K. H. Kim, J. E. Schutt-Aine, “Analysis and modeling of hybrid planar-type electromagnetic-bandgap structures and feasibility study on power distribution network applications,” IEEE Trans. Microw. Theory Tech., vol. 56, no.1, pp. 178-186, Jan. 2008.
[16] Ling-Feng Shi, Da-Li Zhou. Selectively Embedded Electromagnetic Bandgap Structure for Suppression of Simultaneous Switching Noise[J]. IEEE Trans. Electromagn. Compat., 2014, 56(6): 1370-1376.
[17]M. Swaminathan, A. E. Engin. Power integrity modeling and design for semiconductor and systems[M]. New Jersey: Prentice Hall, 2007: 17-29.
[18]D. M. Pozar. Microwave Engineering, 4th ed[M]. New York: Wiley, 2012: 48-110.
[19]李君. 系统级封装的电源完整性分析和电磁干扰研究[D] 成都: 西南交通大学, 2010.
本文来源于中国科技核心期刊《电子产品世界》2016年第6期第52页,欢迎您写论文时引用,并注明出处。
射频工程师养成培训教程套装,助您快速成为一名优秀射频工程师...
天线设计工程师培训课程套装,资深专家授课,让天线设计不再难...
上一篇:基于纹波注入滤波方案的超小纹波开关电源设计
下一篇:汽车电源设计挑战及解决方案

