基于Matlab GUI层次分析法的实现和应用

1.层次分析法基本原理

层次分析法(Analytic HierarchyProcess简称AHP)是将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。

层次分析法的主要流程分为四步：一是建立层次分析结构模型，二是构造成对比矩阵并计算权向量，三是做一致性检验，四是计算组合权向量(作组合一致性检验)。

层次分析法的基本思想是把复杂问题分解为若干层次，在最底层次通过两两对比得出各因素权重，通过由低到高的层层分析计算，最后计算出各方案对总目标的权数，权数最大的方案即为最优方案。

决策的实质是进行比较，通过比较做出选择，但是对于缺乏公度性的多目标决策问题来说，由于无法用统一尺度去衡量比较各个不同目标，因此，唯一可行的办法是进行两两比较。通过将两两比较后的结果填入判断矩阵的特征和特征向量，然后确定各目标重要性的加权值。

层次分析方法的基本假设是层次之间存在递进结构，即从高到低或从低到高递进。当复杂系统中某一层次既可直接地影响其他层次，同时又直接及间接受其他层次影响时，就不属于层次分析范围，需要用网络模型来描述。

层次分析的基本方法是建立层次结构模型。建立层次模型，首先要对所解决问题有明确的认识，弄清它涉及哪些因素，如目标、分目标、部门、约束、可能情况和方案等，以及因素相互之间的关系。其次，将决策问题层次化。将决策问题划分为若干个层次，第一层是总目标层，即要想达到的目标;中间层常称为分目标层、标准层、部门层、约束层、准则层等;最底层一般是解决问题的方案或者与问题有关的可能情况，常称为方案层或者措施层。

建立层次模型之后，可以在各层元素中进行两两比较，构造出判断矩阵。判断矩阵是定性过渡到定量的重要环节，再通过求解判断矩阵的特征向量，并对判断矩阵的一致性进行检验，检查决策者在构造判断矩阵时判断思维是否具有一致性。

通过一致性检验后，便可按归一化处理已经处理过的特征向量作为某一层次的加权值，然后从高层次到低层次逐层计算排序加权值，得出层次总排序。

最后是对总排序的一致性检验，通过检验，则其结果可以用于决策;否则，就需要重新调整判别矩阵。

2.Matlab GUI层次分析法软件包实现

虽然利用Matlab的程序语句命令也能实现层次分析法，但是不够简洁直观。结合Matlab GUI设计。编写应用程序，并设计相应的用户界面来实现层次分析法，可以使使用者更加方便快捷的应用层次分析法。

2.1 软件算法流程软件算法流程：开始→输入层数N→输入判别矩阵→一致性检验→(通过)输入准则层与方案层的关联→计算组合权向量→根据组合权向量决策→结束注：若一致性检验不通过，则直接结束。

2.2 关键编程要点

2.2.1 写入txt文件

由于层次分析法需要处理很多矩阵，如果一个个输入会相对比较麻烦，我们采取单独的txt文件形式进行保存。将所有结果保存为txt文件。

关键代码如下：

2.2.2 写入数据

写入所有操作的数据，以便层次分析法操作。

关键代码如下：

2.2.3 输入矩阵

由于层次分析法需要处理很多矩阵，当矩阵阶数小于7时，可以手动输入矩阵;当矩阵阶数大于7时，可以导入excel文件。

关键代码如下：

3.实例应用

根据1中的“选择旅游地”模型，继续求解，得到准则层的判别矩阵：

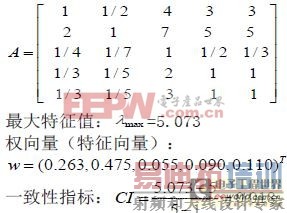
随机一致性指标RI=1.12(查表)一致性比率CR=0.018/1.12=0.0160.1结论：通过一致性检验。

最后用本软件输入数据，得到的结果如图1所示：

4.总结

本文应用实际例子，结合Matlab强大的数学算法功能和GUI的界面设计功能，来解决数学建模过程中的层次分析法问题。由于层次分析法的运用范围极广，如经济计划和管理，能源政策和分配，人才选拔和评价，生产决策，交通运输，科研选题，产业结构，教育，医疗，环境，军事等，说明该软件的应用前景很好。同时，我们的MatlabGUI设计存在着一些优点和不足。不足有：界面设计不够美观、代码不够精炼等。而优点则有：数据多时，矩阵可以利用Excel导入，避免了输入的繁杂;对数据采用文本录入方式，具备存储能力和纠错能力，这点还可以深入探讨。