有源滤波器的特点及分类详解

有源滤波器的频率范围是由直流到500KHZ，在低频范围内已取代了传统的LC滤波器。特别是在很低频率下不可能实现LC滤波器，但有源滤波器却能给出满意的结果。

1、有源滤波器它的输入阻抗高，输出阻抗极低，因而具有良好的隔离性能，所以各级之间均无阻抗匹配的要求。

2、易于制作截止频率或中心频率连续可调的滤波器且调整容易。

3、如果使用电位器、可变电容器，有源滤波器的频率精度易于达到0.5%。

4、不用电感器，体积小、重量轻，在低频情况下，这种优点就更极为突出。

5、设计有源滤波器比设计LC滤波器具灵活性，也可得到电压增益。

但是应当注意，有源滤波器以集成运放作有源元件，所以一定要电源，输入小信号时受运放带宽有限的限制，输入大信号时受运放压摆率的限制，这就决定了有源滤波器不适用于高频范围。目前实用范围大致在100KHZ以内，另一方面，在频率高于100KHZ时，无源滤波器的性能却比有源滤波器的好，当频率高于10MHZ时，无源滤波器则更显得优越。

有源滤波器按通带性能的分类

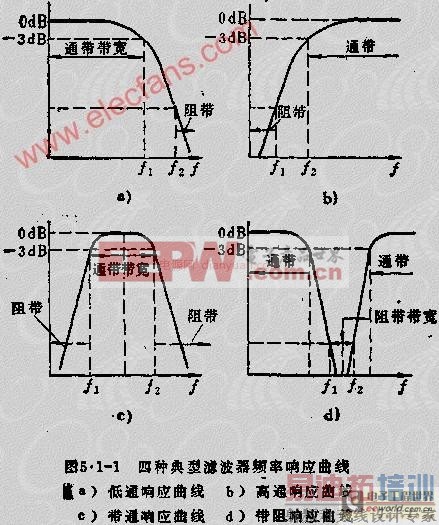
像无源滤波器一样，按通带性能划分有图5.1-1所示的四种类型。即低通滤波器（LPF）高通滤波器（HPF），带通滤波器（BPF），和带阻滤波器（BEF）。以上四种滤波器，又统称为选频滤波器。

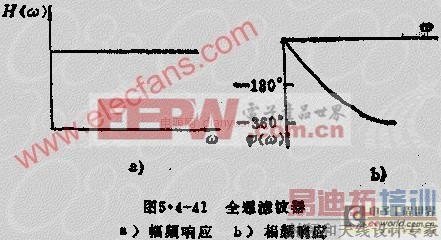
除了选频滤波器之外，还有以相位响应为主要特性的其他一些滤波器，如全通滤波器。它的输出幅度在全频城内是恒定不变的，但输出信号对输入信号的相移却是频率的函数。因此全通滤波器也称为相移滤波器。其幅频响应和相频响应如图4.4-41所示。

有源滤波器以传输特性分类

最平通带“巴特沃斯”响应

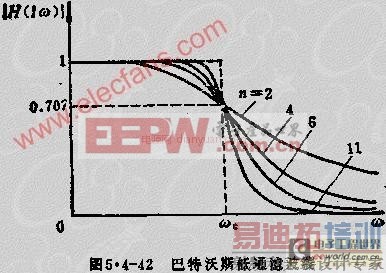
巴特沃斯滤波器的特点是在通带以内幅频曲线的幅度最平坦，由通带到阻带衰减陡度较缓，截止频率以后的衰减速率为6MDB/倍频程，相频特性是非线性的。对阶跃信号有过冲和振铃现象。巴特沃斯滤波器是一种通用型滤波器，又称为最平幅度滤波器，巴特沃斯低通滤波器特性如图5.4-42所示。

通事等波纹“切比雪夫”响应

切比雪夫滤波器的特点是在通带内，具有相等的波纹。截频衰减陡度比同阶数巴特沃斯特性更陡度比同阶数程时的衰减就超过6NDB。在阶数N一定时，波纹越大，截频衰减陡度越陡。相位响应也是非线性，但较之比巴特沃斯为差。切比雪夫低通滤波器特性如图5.4-43所示。

延迟平坦“贝塞尔”响应

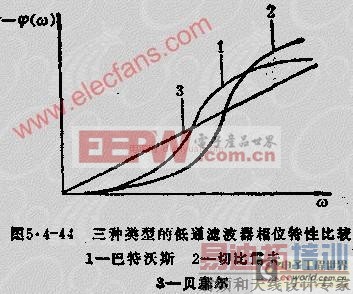
贝塞尔滤波器的特点是延时特性最平坦，幅频特性最平坦区较小，从通带到阻带衰减缓慢。贝塞尔滤波器的幅频特性比巴特沃斯或切比雪夫滤波器差，但从图5.4-44看出，贝塞尔滤波器的相位特性要好得多。贝塞尔滤波器又称为线性相移或恒定延时滤波器。

通阻带等波纹“椭圆函数”响应

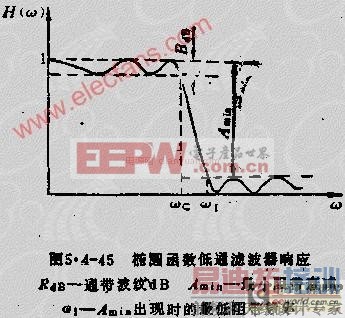
椭圆函数滤波器的特点是在通带和阻带内均出现相等的纹波。图5.4-45示出了椭圆函数低通滤波器响应的幅频特性曲线阻带纹波的出现使椭圆函数滤波器获得了从通事到阻带的最大的衰减速率。若给定滤波器的阶数N，椭圆函数滤波器较其他类型的滤波器具有最陡的截频衰减陡度。但它的延时特性不如前三种好。图5.4-46对上述四种低通滤波器的截频衰减陡度进行了比较。椭圆函数滤波器又称考尔滤波器。

有源滤波器按传输函数的极、零点分类

全极点型滤波器

以上介绍的巴特沃斯、切比雪夫、贝塞尔等三种滤波器，它们的共同特点是传递函数的零点在无限频处。也就是说，这些滤波器只有在无限频处才能给出无穷大的衰减，称之为全极点滤波器。

非全极点滤波器

如椭圆函数滤波器和反切比雪夫滤波器的共同特点是传递函中既含零点也含极点、这样就能在限频处获得无穷大的衰减。以上两种滤波器均是非全极点滤波器。上述滤波器均是非全极点滤波器。

上述滤波器，它们各有特点，在实际应用中，应该根据实际要求来选择滤波器的类型。

如果要求通带响应平坦，对截频衰减陡度要求不太高，阶跃响应允许有过冲的话，则应采用巴特沃斯滤波器。若对幅度平坦性要求不严，而对截止频衰减陡度要求较高的情况，应采用切比雪夫滤波器。而对那此在不失真地再现信号这一要求比衰减特性更重要的场合下，则应采用贝塞尔滤波器。由于椭圆滤波器比其他类型滤波器，才使用椭圆滤波器。对于中等程度要求的滤波器来说，全极点滤波器是完全能满足要求的。