Boost型DC／DC变换器的预测无差拍控制器设计

摘要：为了提升电流模式控制下Boost DC／DC变换器的动态响应速度，采用电流预测和无差拍控制理论对控制器进行设计。给出了线性外插的预测方法和无差拍控制策略，分析了电压环路小信号模型并设计了其控制器。采用前缘调制的预测无差拍峰值电流模式控制，电感电流可以在两个周期内调整到参考量；当占空比超过0．5时，变换器不存在次谐波振荡问题，省去了斜率补偿设计。实验结果表明，与经典电流模式控制器相比，预测无差拍控制器在控制电压上跳变2 V时，能够缩短约22．6％的调节时间；在控制电压下跳变2 V时，能够缩短约9．4％的调节时间。
关键词：控制器；电流模式；预测电流控制；无差拍控制

1 引言
Boost DC／DC变换器的控制问题一直是国内外学术界的研究热点。由于受控对象传输函数的非线性和时变性，传统的控制方法有时不能达到预期效果，故需寻找适合Boost DC／DC变换器的先进控制理论，这包括：模型预测控制、滑模变结构控制、预测电流控制等。
此处采用无差拍控制思想，结合线性外插的预测方法，对Boost DC／DC变换器的电流环进行优化设计，该设计简单可靠，对系统参数不敏感，便于数字方式实现。仿真和实验结果表明，优化后的变换器具有良好的静、动态性能。

2 电流模式控制BOOSt DC／DC变换器
Boost DC／DC变换器是一种能够实现升压的开关电源。电流模式控制通过对电感电流的控制，提升了环路响应速度。对于理想的电流模式控制，环路传输函数已经不包括电感了，因此也就不再有LC双重极点，这就简化了电压环的补偿设计。电流模式控制方式中，峰值电流模式以其具有快速的限流作用而得到广泛应用，因此后面的讨论均基于峰值电流模式。经典的电流模式控制是将电感电流用作脉冲宽度调制器(PWM器)的斜波输入，如图1所示。

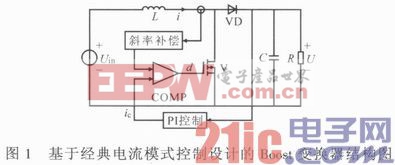
其中，d是占空比，V是开关，VD是二极管，i是电感电流，ic是控制电流。反馈电压通过PI控制器产生ic，与经过斜率补偿的i相比较，进行PWM。经典的峰值电流模式控制存在次谐波振荡的问题，这可通过斜率补偿解决。要保证补偿后的上升斜率大于下降斜率，因此补偿斜率为：

经典电流控制需要采样到连续的电感电流，不便于控制器的数字方式实现；此外，斜率补偿会增加控制电流与电感电流之间的误差，从而降低变换器的动态性能。

3 电流环的预测无差拍控制设计
预测无差拍控制作为一种离散控制理论，是指通过已知状态信息计算出下一时刻控制量，并在数个时钟周期内让目标达到控制量的一类控制方法。由于占空比的计算需使用下个周期的电流和电压状态信息，所以必须对它们进行预测。[p]
3．1 预测方法
预测电压和电流的方法有很多，为便于变换器的数字方式实现，必须采用一种简单有效的预测方法。线性外插的预测方法不仅计算量小，每次预测过程至多需要两次乘法和一次加法，而且对变换器寄生参数不敏感，可得到较精确的预测量。线性外插的预测过程如图2所示。图中，iB1T1，iB1T2为采样电流；upre，ipre分别为预测电压、电流；uB1T1，uB1T2为采样电压。

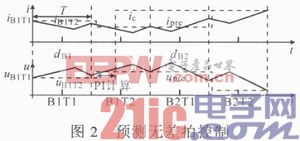
线性外插法的预测方式可表示为：
ipre=2iB1T2-iB1T1，upre=2uB1T2-uB1T1 (3)
该方法需采样两个电流值进行预测，考虑到延迟，在采样第二个值后已经不能计算当前周期的占空比，这决定了每个控制节拍必须包含两个开关周期。
3．2 控制策略
预测电压经过PI控制器得到控制电流，根据控制电流与预测电流之间的误差就可计算出下个节拍的占空比。Boost变换器电感两端的电压在开关导通期间为Uin，在开关关断期间为U-Uin，因此，经过两个相同占空比的周期，电感电流的变化量为：

与经典的峰值电流模式控制相比，预测无差拍控制可在两个开关周期内将电流调整到控制量，提升了动态响应速度；此外，采用前缘调制的变换器不存在次谐波振荡的问题，节省了斜率补偿设计；最后，线性外插的预测方法不仅计算量小，便于变换器的数字方式实现，而且对系统参数不敏感，具有很好的鲁棒性。

4 电压环控制设计
电流模式通过对电感电流的控制，改变了系统的极点，受控对象的传输函数由二阶变成了一阶，因此电压环的补偿变得简单，一般采用经典的PI控制。应用在Boost变换器中的无差拍控制结构如图3所示。

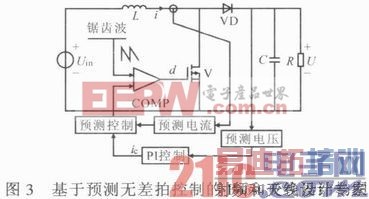
图中，用线性外插法得到预测电流和预测电压，用预测电流与控制电流的误差计算下个控制节拍的占空比。环路中各模块的传输函数为：G1(s)为从i到U的传输函数，G1(s)=(1-d)(-sLeq+R)／(RCs+2)；G2(s)为ic到i的传输函数，G2(s)≈1；H(s)为PI控制的传输函数，H(s)=(KpTis+Kp)／(Tis)；

由于电压环包括：电压预测器、PI控制器、采样器和变换器，因此其开环传输函数为：
L(s)=Hs(s)Hpre1(s)H(s)G1(s) (6)[p]
当穿越频率fc远低于开关频率且远高于RC极点时，式(6)在fc附近可近似为：

将fc设在1／5的右半平面零点处，令式(7)的模值为1，相位裕度为63°，即可算出Ti，Kp。因为L(s)亦即理想电流模式控制下的环路传输函数，所以这样的设计同样适用于经典电流模式的PI控制。

5 仿真结果
以Boost变换器为控制对象，仿真模型参数为：Uin=6 V，U=12 V，f=50 kHz，L=250μH，C=66μF，R=40 Ω。可得到PI控制器参数：Ti= 0．000 25，Kp=1。当控制电压由11 V阶跃到12 V时，控制电流和电感电流的响应如图4a所示；采用相同的PI控制参数，设计预测无差拍控制器和经典电流模式控制器，仿真得到输出电压响应如图4b所示。

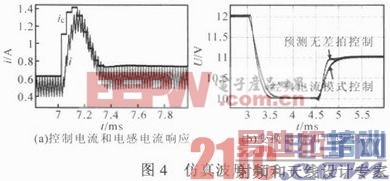
当控制电压由12 V阶跃到10 V时，预测无差拍控制器需要约0．5 ms的调节时间，而经典电流模式控制器需时约0．7 ms；当控制电压由10 V阶跃到11 V时，预测无差拍控制器需要约0．3 ms的调节时间，而经典电流模式控制器需时约0．5 ms。

6 实验结果
按照上述仿真参数构建实验系统。图5示出两种控制方式下，控制电压跳变2 V时，变换器输出直流电压U和交流电压u的响应。

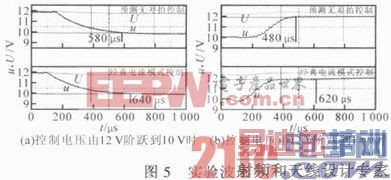
取阶跃量的5％为误差容限，则响应达到并保持在终值0．1 V波动内所需的时间就是调节时间。由图5a可知，当控制电压下跳变2 V时，预测无差拍控制器需要580μs的调节时间，而经典电流模式控制器需要640μs的调节时间。
由图5b可知，当控制电压上跳变2 V时，预测无差拍控制器需要480μs的调节时间，而经典电流模式控制器需要620μs的调节时间。实验结果表明，相比经典电流模式控制器，预测无差拍控制器在控制电压上跳变和下跳变2 V时，分别能够缩短约22．6％和9．4％的调节时间。

7 结论
此处设计了预测无差拍控制，并与经典电流模式控制进行了对比。仿真和实验结果表明，预测无差拍控制器可以改善系统动态性能。该设计方法简单可靠，对系统参数不敏感，便于数字方式实现。