- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
高频和微波功率基准及其应用研究----微量热计基本理论研究( 二)
2.3.1升温方式微量热计
起初的升温方式微量热计,热电堆安放位置和量热计相同,都在热敏电阻座的外面,后来的设计做了改进,将它移到与热敏电阻座紧密连接的波导法兰盘处。这样更容易在不妨碍热电堆工作的前提下,移走热敏电阻座,从而减少误差。
根据定义和式(2-12),直流替代功率可表示为
其中Psub代表直流替代功率,VRFoff和VRFon是在加入高频和微波功率前和加入高频和微波功率后,电桥平衡时热敏电阻两端电压,R是由电桥设置的热敏电阻的直流工作电阻值。
根据经典理论,理想情况下的直流替代功率等于热敏电阻吸收的高频和微波功率,有效效率可表示为
与2.2.1中介绍的量热计理论一样,设K为热电堆对热敏电阻功率座吸收功率的响应系数,电压e2和e1分别是,当输入高频和微波功率和不输入高频和微波功率时,热电堆的电压,则有
热敏电阻座壁的损耗为
由式(2-15)至式(2-18)四式可推导出如下公式计算有效效率ηeff
式(2-19)是升温方式微量热计测量有效效率的基本公式,实际的微量热计系统,还需要考虑隔热传输线损耗对热电堆输出的影响,以及热电堆对直流功率和微波功率响应系数的差异,一般需要对式(2-19)的结果乘以一个修正系数。由于热电堆输出电压和热敏电阻两端电压的测量误差较小,因此测得隔热传输线损耗对热电堆输出的影响和评价热电堆对直流功率和微波功率响应系数的差异成为设计和实现升温方式微量热计的技术关键。
2.3.2等温方式微量热计
等温方式微量热计的结构和2.2.2中介绍的等温方式量热计类似,也是保持量热体温度不变的自动反馈方式,此时的量热计是热敏电阻座体。图2-6是等温方式微量热计的结构示意图。
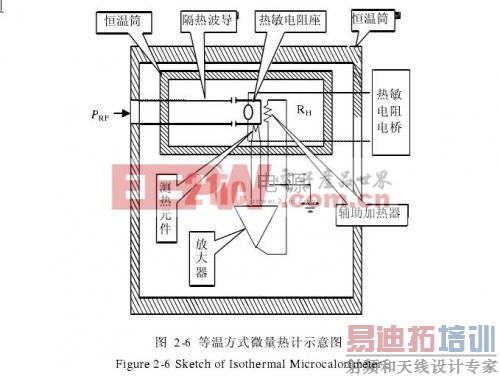
图2-6中的测热元件用来检测热敏电阻座的温度变化,再将变化放大后输入辅助加热器,通过调整直流辅助加热功率,保持座体温度不变。
设计和实现等温方式微量热计的技术关键是保持热敏电阻座体温度不变和消除隔热传输线损耗对直流辅助加热功率的影响。
2.4经典理论的不足和完善
前面介绍的微量热计经典理论的主要不足之处在于,当将热敏电阻功率座用作量热体时,没有考虑热敏电阻本身的有源特性对量热的影响,特别是与微量热计中其他无源部分的相互影响,只是简单的将量热计的理论直接用于微量热计的热分析,根据经典理论建立的微量热计会带来一项新的系统误差——热等效误差。
2.4.1热敏电阻功率座
将热敏电阻功率座有效效率的定义式(2-14)改用符号表示如下
其中Psub为直流替代功率,是加入和关闭高频和微波功率后热敏电阻上的直流功率差,分母Pnet是加入高频和微波功率后损耗在热敏电阻功率座中的总的高频和微波功率。
热敏电阻座的效率也可以根据式(2-13)改用符号表示如下
其中P TRF是热敏电阻吸收的高频和微波功率。
一直以来有效效率被看作对热敏电阻座自身特性的描述,与热敏电阻座的工作条件无关,基于这一特点,人们在微量热计中测量得到热敏电阻座的有效效率后,热敏电阻座被取出用作工作标准,根据其有效效率测量微波功率。
但比较式(2-20)和(2-21)可以看出,效率的定义只与热敏电阻功率座结构有关,有效效率的定义不仅与热敏电阻座的特性有关,还依赖于直流替代功率。在后面的分析中,我们会发现式(2-20)并不能保证有效效率值的唯一性,有效效率不仅与所加功率时间有关,还与热敏电阻功率座自身及所在传热环境的换热特性有关。
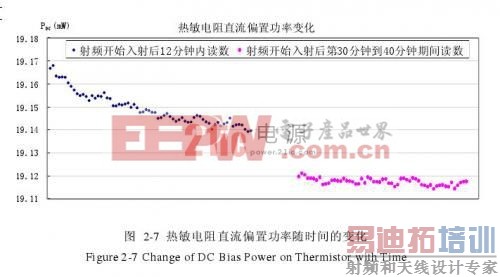
图2-7给出了某商用热敏电阻功率座在加入10mW微波功率30秒后的直流偏置功率变化情况。由图可知,热敏电阻的直流偏置功率从19.17 mW开始下降,在11.5分钟后为19.14 mW,相应的直流替代功率增加了约29μW;39.5分钟后热敏电阻的直流偏置功率基本不再下降,约为19.115 mW,直流替代功率又增加了约25μW.若假设该热敏电阻座在第30秒时刻直流替代功率为10mW,根据式(2-20),座的有效效率在微波功率输入的第12分钟和第40分钟时,相对于第30秒时刻分别增加了0.29%和0.54%.
这无疑给功率测量带来了很大的混乱,因为无法判断何时的有效效率是正确的。实际上,重新考察式(2-20)和(2-21)可以发现,混乱的来源是直流替代功率的定义。对应式(2-21),式(2-20)中的Psub应为加入微波功率时热敏电阻上对高频和微波功率的直流替代功率。为区别于人们一直采用的式(2-20),这里定义了一个新的量——真有效效率,其定义式如下其中ηteff代表真有效效率,PRFsub为加入高频和微波功率时热敏电阻上对高频和微波功率的直流替代功率。
为区别于人们一直采用的式(2-20),这里定义了一个新的量——真有效效率,其定义式如下
其中 ηteff代表真有效效率,PRFsub为加入高频和微波功率时热敏电阻上对高频和微波功率的直流替代功率。
相应的,不再使用热敏电阻功率座的替代效率,而采用热敏电阻的替代效率ηsub,则有这样,真有效效率和效率的关系为
由于目前使用在热敏电阻座中的热敏电阻均是珠状结构,直径约为0.05毫米,且表面并没有封装,高频、微波和直流信号在热敏电阻中分布不同导致的误差很小,NIST的研究表明这项误差小于0.01% ,本文中始终认为ηsub =1,所以ηteff=ηs。因为研究表明,在采取适当的措施后泄漏的微波功率可以忽略不计,所以Pnet可表示为
其中Ploss是损耗在功率座内壁上的高频和微波功率。
从热敏电阻座的直流替代原理来看,由直流平衡电桥偏置着的热敏电阻在高频和微波功率入射后经历了两个过程,真有效效率和有效效率分别描述了热敏电阻座在两个不同过程内的特性。
1)过程1:高频和微波功率进入功率座,由于热敏电阻的热容极小,直流平衡电桥的时间常数很小,如图2-8所示,用于美国NIST的N型同轴热敏电阻功率座对高频和微波功率输入的响应平衡时间小于6ms.在如此短的时间内其他因素的影响可以忽略不计,平衡电桥在很短时间内达到重新平衡,平衡时PRFsub =Psub,ηteff =ηeff =ηs。
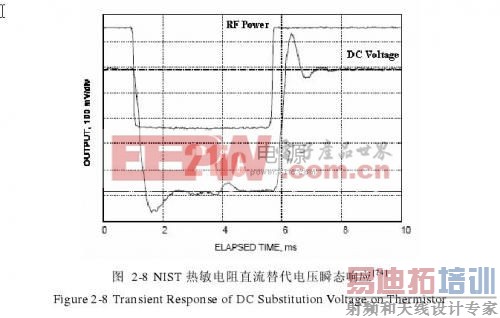
2)过程2:在过程1完成后,功率座壁等热敏电阻的周围环境与热敏电阻的热交换的影响开始显现,PRFsub≠Psub,有效效率开始偏离真有效效率,ηteff≠ηeff,图2-7显示的就是这一过程。
从以上分析可以看出:
1)由于时间短,在过程1不能进行高准确度的测量,也就不能直接测量得到真有效效率或效率。
2)在过程2中,有效效率和真有效效率有偏差,偏差会随时间变化。
为此,需要分析热敏电阻座的传热特性,研究有效效率和传热特性的关系,解决在过程2中有效效率与真有效效率的偏差问题,这里的传热特性是指在量热计分析时已经用到的热导、热阻和热容等描述物体热传递特性的物理量。为避免混淆,在后面的分析中,将用效率代替真有效效率作为评价有效效率的参考。
图2-9是热敏电阻功率座传热结构示意图。
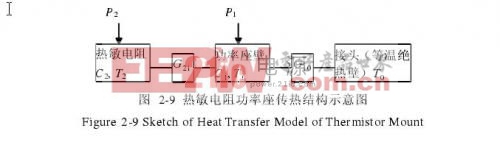
其中C2,T2分别是热敏电阻的热容和温度,C1,T1分别是功率座壁的热容和温度;G21和G10分别是热敏电阻与功率座壁之间、功率座壁与所连接传输线之间的热导;T0是热敏电阻功率座所连接传输线的温度,由于热敏电阻功率座总是连接在等温绝热壁上(等温绝热壁采用绝热的大热容设计或恒温设计)或有大热容和大热导的传输线上,可以认为T0始终不变。P2和P1分别是作用在热敏电阻和功率座壁上的总功率,包括了直流功率P2DC、P1DC和高频、微波功率P2RF、P1RF。
根据传热学原理,描述该系统热平衡过程的方程式为
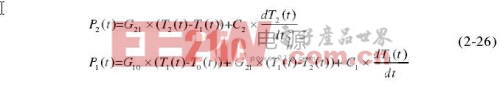
根据热敏电阻功率座的工作原理,可以将其功率测量过程分成两个阶段,第一阶段是直流偏置阶段,第二阶段是高频和微波功率替代阶段。第一阶段由平衡电桥提供直流功率,达到平衡状态后,热敏电阻被偏置在一个固定的直流电阻下,其温度也保持不变;由2.4.1可知,第二阶段实际包括了两个过程:首先在第一阶段平衡状态的基础上,加入高频和微波功率,在平衡电桥的作用下,直流偏置功率减小,迅速达到重新平衡,完成了热敏电阻上高频和微波功率对直流功率的替代;第二过程是在前一过程平衡的基础上,功率座壁与热敏电阻的热交换开始影响直流偏置功率。因为前一过程时间很短,可以将两个过程作为一个阶段处理。在下面的推导中,该阶段的直流偏置功率均是指过程1完成后的直流功率,而且认为T2始终不变。
令第一阶段电桥平衡后的直流偏置功率与第二阶段的直流偏置功率之差为ΔP2DC,ΔP2DC即直流替代功率Psub。由于直流偏置功率受热敏电阻与功率座壁热交换影响而随时间变化,所以Psub也是第二阶段时间的函数。在下面的推导中,将用Tij表示第i个位置第j个阶段达到稳态时的温度,用PiDCj表示第i个位置第j个阶段达到稳态时的直流功率,位置0、1、2分别指所接传输线、功率座壁和热敏电阻。
2.4.2 微量热计中的有效效率
由2.3可知,微量热计有两类工作方式,等温方式和升温方式。下面针对两类方式分别进行分析。
2.4.2.1等温方式
等温方式微量热计的结构如图2-10所示。
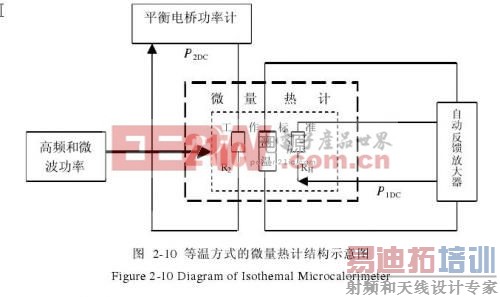
[p]
所谓等温是指由测温元件、直流辅助加热器和反馈控制组成反馈控温环路,在加退高频和微波功率过程中始终保持T1不变。
在直流偏置阶段,未加入高频和微波功率,只有直流功率,P2 =P2DC(t),P1 =P1DC(t)。达到初始平衡后,P2 =P2Dc1,P1 =P1Dc1,有
在高频和微波功率替代阶段,加入高频和微波功率后,P2 =P2RF +P2DC(t),P1 =P1RF +P1DC(t),则有
将式(2-27)代入式(2-28),可得
其中P2RF和P1RF分别是热敏电阻和功率座壁上吸收的高频和微波功率,即式(2-25)中的PTRF和Ploss。
由于热敏电阻平衡电桥和反馈控温环路的作用,T2始终不变,T1也始终不变,令第一阶段电桥平衡后的辅助加热功率与第二阶段的辅助功率之差为ΔP1DC,化简式(2-29)有则
有效效率为
即有效效率始终与效率相等。
2.4.2.2升温方式
升温方式微量热计的结构如图2-11所示。
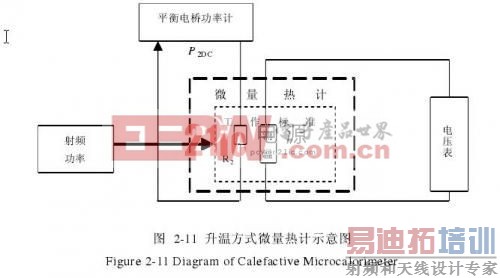
所谓升温是指在这种设计中,没有反馈控温环路,加入高频和微波功率会导致T1的变化,由于T1稳态温升与P2DC及Ploss的比例系数可以求得,就可以根据加入高频和微波功率后的稳态温升计算Ploss。
在直流偏置阶段,没有输入任何功率时,热敏电阻、功率座壁和等温绝热壁的初始温度相等,为T0;当加入功率时,只由热敏电阻平衡电桥提供直流功率,P1 =0;达到初始平衡后,P2 =P 2DC1,则有
由此得到功率座壁在本阶段的稳态温升为
在高频和微波功率替代阶段,加入高频和微波功率后,P2 =P2RF+P2DC(t),P1 =P1RF,由式(2-26)得
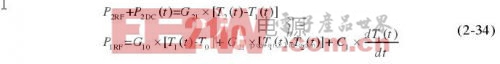
式(2-32)和式(2-34)联立,可解得在本阶段功率座壁温升的表达式

及
则有效效率为

有效效率与效率之差为

达到稳态后,有效效率为
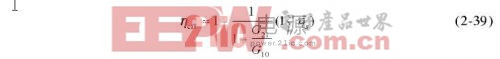
有效效率与效率之差变为

根据式(2-40)计算得到的有效效率与效率偏差曲线如图2-12所示。
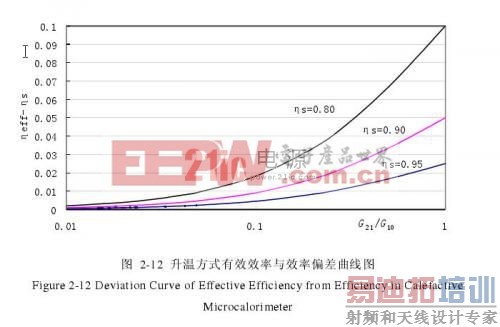
其中从低到高依次是效率ηs为0.95、0.9、0.8时有效效率与效率的偏差随G21/G10变化的曲线,由图2-12可见采用升温方法测量的有效效率总是大于效率,对ηs较小的功率座,两者差异较大;对同一个功率座,ηs和G21固定,G10是影响二者差异的原因。
式(2-37)是升温方式有效效率的理论表达式,但不能用于有效效率的测量,因为在测量时能够获得的测量数据只有ΔP2DC(t)和ΔT1(t),无法使用式(2-37)计算有效效率,还是需要达到稳态才能计算出稳态时的有效效率。
达到稳态后,功率座壁在本阶段的稳态温升可由式(2-35)可求得。
式(2-34)变为

即得
则有效效率的稳态表达式式(2-39)也可以写为
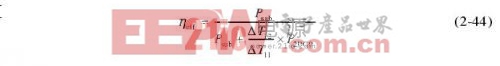
根据式(2-44)就可以使用实际测量结果计算有效效率的稳态值
射频工程师养成培训教程套装,助您快速成为一名优秀射频工程师...
天线设计工程师培训课程套装,资深专家授课,让天线设计不再难...
上一篇:基于MOSFET设计优化的功率驱动电路
下一篇:高频和微波功率基准及其应用研究----微量热计基本理论研究(
一)

