为什么功率最大意味着灵敏度最低？

　　对于各种滤波器设计和网路理论问题进行深入探讨是值得关注的话题。本文在此讨论的主题为採用双端接LC梯型滤波器的拓朴结构。首先，我必须将来源电阻和负载电阻设置为相同的值。由于电感器和电容器构成的网路具有两个‘埠’，以供讯号进入和离开网路。在我们的滤波器中，输入埠从具有特定电阻值的来源处获得讯号（一般无法变更），输出埠则连接到由另一个电阻构成的‘负载’（通常可以加以控制）。

　　图1显示的是範例滤波器。其输出端设计採用与来源电阻值一样的电阻端接。图2显示的是非常良好且平坦的通带响应。图3显示在移除端接电阻后的较差响应。

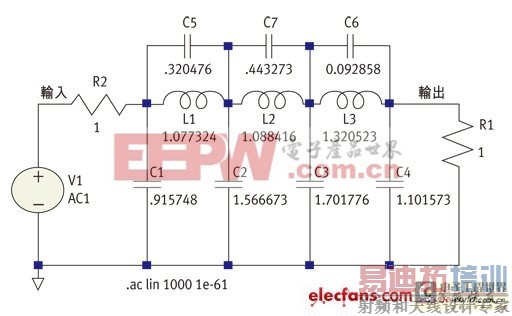
　　图1： 双端接低导通滤波器网路範例。

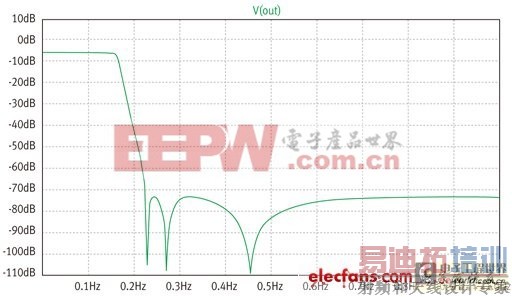
　　图2：图1元件在具有负载电阻时的电压增益。

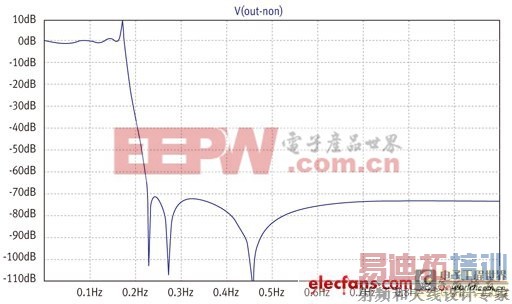
　　图3：图1元件在无负载电阻值时的电压增益。

　　我们可以看到，对于本文所用的特定元件值，低涟波平坦响应只有在加入负载电阻的情况下才会出现。但这并非是具有两个电阻的结果。图4是在无负载电阻情况下产生同等振幅响应（图5）的网路值集合。其电压增益为0dB，而非6dB。但你是否真的会在大多数实际情况中使用该滤波器？答案不言而喻，因为响应相同，而增益更大，而且可以节省一个元件，谁不喜欢呢？

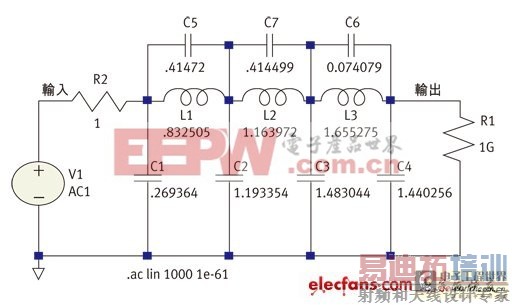
　　图4：无负载电阻的各种元件值组合。

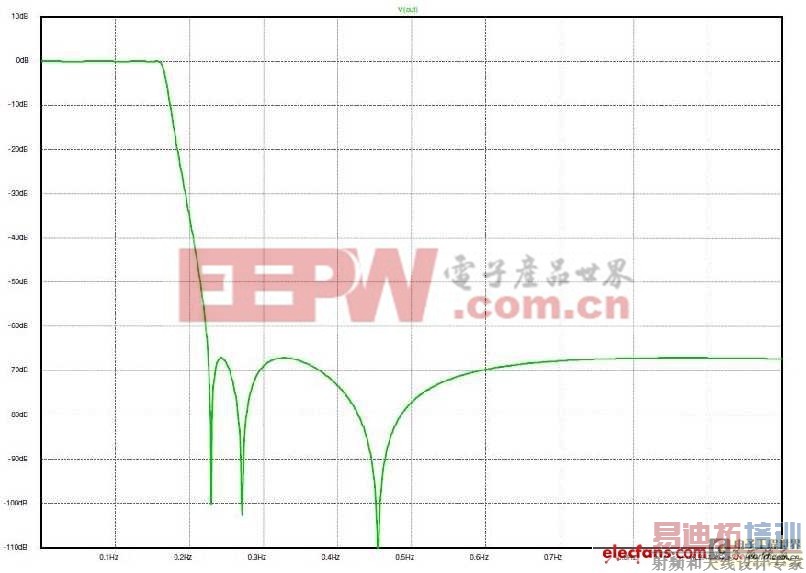
　　图5：无负载电阻时，响应依旧非常出色且平坦。

　　图6和图7说明了我们抗拒採用‘单端接’诱惑的塬因。这两张图是元件值在±5%允许範围内变化时，100个响应曲线叠加在一起的状况。我们可以清晰地看出双端接滤波器更能够适应所使用元件值的小幅度变化。在下文中还可以看到当我们使用某些扩展技巧时──在不使用这些电感器的情况下，以这些网路为‘塬型’构建主动滤波器──这种特性仍然得以保留。

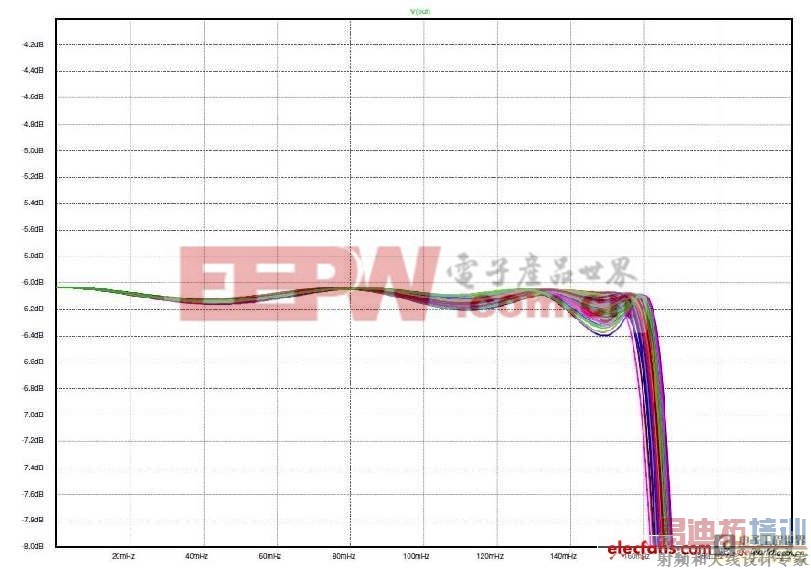
　　图6：对图1值的蒙特卡罗分析。

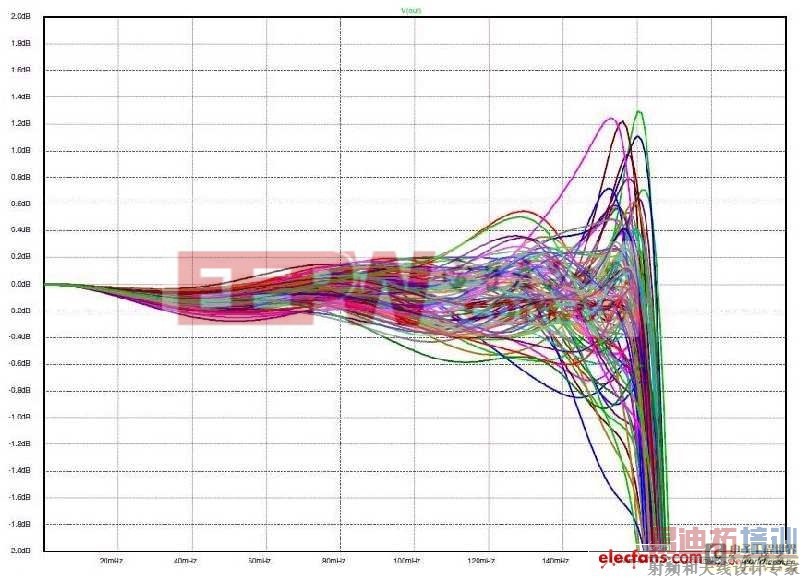
　　图7：对图4值的蒙特卡罗分析。

　　双端接滤波器有什么特别之处呢？要回答这个问题，我们必须考虑当讯号从来源电阻通过LC网路到负载电阻时时，到底发生了什么？

　　稍微岔开一下话题。想像一下你正在面试一个类比设计职务，并要求回答下面的问题：

　　“你有一个50欧姆输出阻抗的正弦波产生器，开路的情况下可以输出1Vrms的电压。客户给你一个输入阻抗为3.3K欧姆的黑盒子；如果该黑盒子要能正常工作，需要至少3Vrms的50KHz输入讯号。你必须让系统工作，但却没有电源。你在实验室唯一能够使用的电子元件是双导线的被动元组件。请说明如何解决上述问题及其工作塬理。”（案例1）

　　那么这个挑战就在于没有电池或太阳能电池，也没有电晶体或整合电路，而且肯定也没有变压器。在继续读下去之前（特别是你準备参加面试的情况下）请先好好想想。也许我们可以从图2找到一些灵感。想到了吗？这裡有个适用的解决方案：

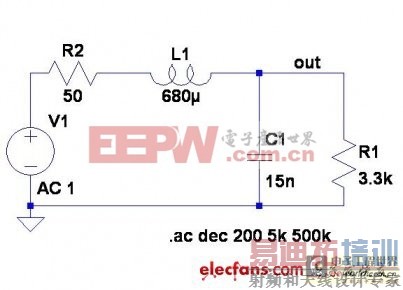
　　图8：适合案例1的解决方案。

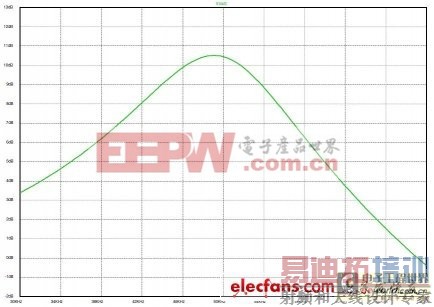
　　图9：图8解决方案的频率响应

　　我们只使用被动双导线元件构建一个高Q值的低导通滤波器。图9显示的是讯号产生器上设置为1Vrms开路输出到黑盒子电压的全频段状况。我们明确地实现了让系统在规定频率上工作的电压增益。那么，哪儿可找得到免费的午餐呢？

　　当然什么地方都不会有。但我们可以问个问题：“我们能够从这类解决方案中得到的最大电压增益值是多少？”要得到结果，首先要认识到，虽然从这样的元件组合中得到电压增益是常见的，但不可能得到功率增益。这就是理解这些被动滤波器网路的关键所在：功率进入网路，然后离开网路。如果来源能在特定输出电阻上提供特定的输出电压，对于连接的负载而言，能够耗散的功率有严格的上限。你可能在学校中学习过最高功率塬理（Maximum Power Theorem），但却未曾多加注意。但对被动滤波器而言，这个塬理非常重要，今后请予以相当的关注。

　　你可能已经想起来了，实现最高功率传输的条件是负载电阻和来源电阻相等。你可以使用大学？媥ガ鴘漪燥无味的微积分来证明。先用一个叙述来表达负载电阻上耗散的功率，根据负载电阻RL计算该功率的导数。将导数设为0，然后求解RL。

　　是不是一下子就豁然开朗了？你首先想到的是用变压器。这是让负载电阻与来源电阻匹配的传统方法。在理想的情况下，变压器可以把功率从来源无损地传输到负载，不过它一般用于电压、电流不同的情况下。使用适当的匝数比（turns ratio），不论负载电阻值是多少，都可以在理想的情况下在负载电阻上获得相同的耗散功率。

　　这就是我们对图8的LC滤波器网路採用的措施：我们导入了一个变压器。所有进入LC网路的功率又出去了。在採用正确元件值的情况下，我们可让所有功率在特定频率上全部到达负载上，而无论负载的值是多少。

　　如果我们可以使用变压器或者变压器的等效LC线路，我们可以计算出50欧姆来源和3.3K欧姆负载之间能够获得的最大电压增益。所需的电压转换等于阻抗比的平方根，在本例中为8.12倍。将该比例与我们在等效电阻端接例子中的电压增益0.5相乘。所以在任意LC值下可以得到的最大增益为4.06倍，或者大约12.2dB。图10显示以我们自製的变压器任意选择1，000种不同的L和C值得到的结果。响应曲线的峰值从未超过预计值。至于为什么不是每个频率下所有功率都耗散在负载上？那是因为部份功率被反射回来源。

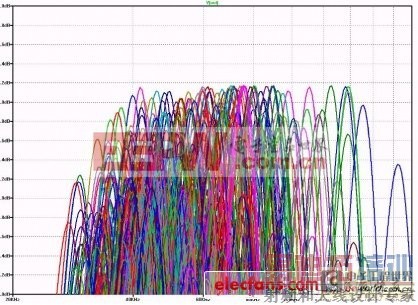
　　图10：响应曲线的峰值从未超过预计值。

　　所有射频工程师都开始不耐烦地打哈欠了，因为这对你们来说相当稀鬆平常。设计LC网路，确保让所有来源的功率传输到负载，是一项称之为阻抗匹配的核心射频技术。这确实像两个不等效电阻之间的滤波器设计（每种设计方案都有其伴随的想像部份需要加以考虑）。一般是用L和C来完成的，而非体积庞大、成本高昂的变压器。除了微波频段外，其中的变压器体积不大、价格也不高，不过当导体靠得太近的时候，就会造成谐振波峰。

　　现在回到我们最初讨论的问题。为什么一个（正确设计的）双端接滤波器具有如此优越的‘灵敏度’特性？这是因为对于滤波器通带内的一个或者有时多个频率，它工作在功率传输的最大可能点上。请再次观察图6和图7。在双端接滤波器情况下，元件值的任何变化只会让功率传输（随之为电压增益）下降而非上升。在被称为反射零点的特定关键频率上，滤波器响应的‘灵敏度’与网路中每个反应元件呈抛物线函数的下行关係。这样就很难让网路的响应比没有应用功率传输约束时更差。后者状况指的是单端接的时候，或者任何滤波器的设计响应未能满足最大功率增益值的时候。要得到最高功率增益值，可以抛开滤波器，使用变压比较为合适的理想变压器。

　　还有一个问题。我们在开始的时候曾经比较过两种滤波器，其中一种滤波器的负载电阻与来源电阻相等，另一个则没有负载电阻。我们能否针对在特定来源电阻和负载电阻的比率下成功设计出低灵敏度、相同频率响应的滤波器？有时候是可行的，但至于我们的低导通滤波器案例则不能。对于特定的响应，我们需要平坦的响应，让DC增益与那些‘触点’最大值相等。这就意味着在该极低灵敏度的滤波器中，来源电阻和负载电阻必须等值。对于更加普遍的情况而[p] ，如果不需要对通过的0频率或者无穷频率施加特定的衰减，通常可以设计出任意两个阻抗间的最低灵敏度（即最匹配的）滤波器。至于如何实现，其方法足够写上几本书，不过初学者就不用看了。

　　我想你现在已经感受到最高功率传输的神奇，以及它如何为设计某些高阶且可实际製作的滤波器找到了可行途径。未来我们还会就这个问题做进一步的讨论。