- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
集成运放组成的电压比较器电路
集成运放组成的电压比较器电路:
1. 功能及应用:主要用来判断输入信号电位之间的相对大小,它至少有两个输入端及一个输出端,通常用一个输入端接被比较信号Ui,另一个则接基准电压VR 定门限电压(或称阀值)的UT。输出通常仅且仅有二种可能即高、低二电平的矩形波,应用于模-数转换,波形产生及变换,及越限警等。
2. 运放的工作状态:开环和正反馈应用:运放在线性运用时,由于开环增益一般在105以上,所以其对应的输入的线性范围很小,Ui数量级,为了拓宽其线性范围就必须引入负反馈,降低其开环增益。二比较器则希望其输入的线性范围越笑越好(即比较灵敏度越高)采用开环或使开环增益更高的正反馈应用。在儿有必要重复展现运放开环电压传输特性。见图8.2.1,请注意横、纵坐标标度的不同
(1) 从途中可化称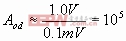
(2) 若Ui发出变化,使Uo从负波饱和值突变到正饱和值,只在经过极窄的线性区时,才遵循在线性工作时才特有的“虚短”,其它时刻“虚短”不复存在。
(3) 若横坐标采用与纵坐标相同的标尺,则线性部分特性与纵轴合拢。
(4) 若用正反馈使Aod↑,则可缩短状态的转换时间。
3. 分类:
(1) 单限比较器
(2) 迟滞比较器(Schmitt)
(3) 双限比较器(窗口比较器)
二. 单限比较器
1. Ui与UR分别接运放两输入端的开环串接比较器,见图8.2.2
ΔUi>UR Uo=+Uom
ΔUiR Uo=-Uom
ΔUi=UR Uo发生翻转(或称突变)
UT=UR 门限电压或阀值,若UR=0称为过零比较器
Δ当Ui与UR互换位置,此时Uo以Ui=UR为对称轴与交换量对称。
2. Ui与UR并联在运放同一输入端时的开环并接比较器 见图8.2.3 [p]
[p]
Δ在同相端可作Therenin等效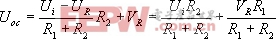
当Uoc>0时,即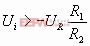
Uo=+Uom
当Uoc
可见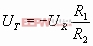
Δ若把运放的同相端
与反相端互换,则与图8.2.2(b)类同
三. 迟滞比较器(正反馈比较器)
其特点
抗干扰能力较强。在单限比较器种,如果Ui受到干扰,在阀值附近回出现Ui+ΔUi(干扰信号多出现在阀值电压上,下波动,以致出现条纹误翻转,而迟滞比较器利用其传输特性的回差电压,输入的干扰信号不能使状态误翻转。
1. 两种迟滞比较器的传输特性 见图8.2.4
动画演示
Δ同相型:Ui接运放同相端
反相型:Ui接运放反相端
Δ均由二根传输特性(1),(2)合成,同相型. 当Ui从低值↑≥UTH,Uo从UOL↑UOH;当Ui从高值↓≤UOL时,Uo从UOH↓UOL。反相型则类同。
Δ UTH,UTL为二个阀值,ΔUT(回差)=UTH-UTL
Δ |UOH|=|UOL|或|UOH|≠|UOL|根据输出是否有箝位电路而定。
2. 二种基型迟滞比较器
(1) 反相型迟滞比较器 见图8.2.5
Ui=U-,Uo被箝位在±UZ,避免运放计入过饱和。
假设Ui在足够低时,Uioff=+UZ (始终稳定)
此时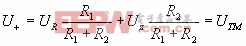
Δ当Ui从低值↑ 若Ui≥U+时,Uo从+UZ↓ -UZ
此时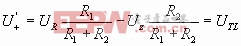
Δ当Ui从高值↓至Ui≤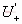
,Uo从-UZ↑+UZ
Δ门限宽度ΔUT=UTH-UTL=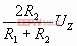
Δ当UR=0时,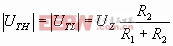
ΔUi无论从足够低或足够高单调增加或单调减少,Uo仅翻转一次,即过了阀值后就维持在一种稳态。
(2) 同相迟滞比较器 见图 8.2.6 [p]
[p]
UR=U-
设Ui足够低,使U+R,Uo=UoL=-UZ (初始稳态)
若要使Uo从-UZ↑+UZ,必须使Ui↑,以致使U+≥U-=UR才行,此时对应的Ui=UTH
Δ当Ui从低值↑,使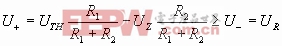
即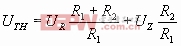
此时Uo从-UZ↑+UZ
Δ当Ui从高值↓,使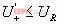
时所对应的Ui=UTL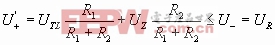
即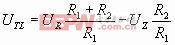
此时Uo从+UZ↓-UZ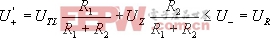
同上面反相型类同,Ui单调升或单调降,Uo只改变一次状态,过了阀值后只维持在一种稳态上。
四. 双限比较器 (窗口比较器)
其特点是Ui单调升或单调降,Uo均有两次突变,与单限比较器和迟滞比较器有区别,因此它可以判别Ui是否在两个电平之间。它实际上由二个单限开环比较器组成,D1,D2作用为隔断,Uo1,Uo2连接通路,避免Uo1,Uo2极性相反时,互为对方提供低阻通路而造成运放损坏。
ΔUiRL(RH)
ΔUi>URH(>URL)
ΔURLiRH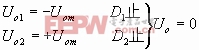
Δ采用上面窗口比较器可以区分三极管β是否在需要范围内,比如记为合格范围为 50100均要取出,则可用发光二极管亮表示一种越限极警,不亮记为可通过即β合格。
Δ改接一下上述输入输出回路即方便可得
要区分β=50,100 找出时应得URL及URH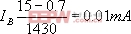
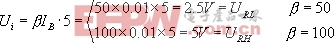
对应图 8.2.7(b) 传输特性可画出β与Uo的关系
即
射频工程师养成培训教程套装,助您快速成为一名优秀射频工程师...
天线设计工程师培训课程套装,资深专家授课,让天线设计不再难...
上一篇:技术分析:智能化的网络UPS系统
下一篇:boost升压电路工作原理

