脉冲变压器的磁学

摘要:详细阐述脉冲变压器的应用及高频脉冲变压器设计所需了解的磁学参数、变压器的综合等效电路和变压器的测试方法。

Abstract: This paper explains in details the application of pulse transformer, the magnetic parameters to be learnt before designing high frequency pulse transformer, the integrated equivalent circuit of transformer and the measurement of transformer.

关键词:脉冲变压器磁学频率响应特性

Keywords: Pulse transformer， Magnetics， Frequency response characteristics

1引言

变压器通常有电源变压器和信号变压器两大类。

磁性元件是电源开关变换器和信号变压器中的必备元件。由于磁材料特性的非线性，其特性对温度、频率、气隙的依赖性使得磁材料参数测量较为困难，因此在进行磁元件设计时，需要对磁元件的参数、一般特性和设计方法有一定的了解。首先，本文的主要部分叙述变压器磁学的基本理论和磁学定理、参数的含义和解释。其次，叙及变压器的性能模型和等效电路，对变压器的各种参数和术语进行解释。还对设计高频开关电源时遇到的高频电流效应问题作一简介，最后对变压器测试时所用到的变压器等效电路参数的测量方法作一些叙述。

为了领会实际变压器在应用时的性能，在纯电阻负载的情况下，用变压器宽带信号的频域响应特性，推导出实用的一般等效电路模型。

时域响应特性曲线最能说明等效电路参数对加在其上脉冲波形的上升沿、峰值和下降沿的影响。对采用高重复率数字脉冲信号的局域网（LAN）和长途通信来说，变压器对这种脉冲信号的响应是应特别重视的。

2变压器磁学的基本原理

2.1法拉弟定律

电和磁相互之间有着紧密的联系。磁场是电荷（电流）运动的结果。反之，如果把一根导体放在随时间变化的磁场里，在导体上就会产生感应电动势(emf)。法拉弟定律指出这个感应电动势是和磁通量的变化率成正比的。

e=－dψ/dt=－NdΦ/dt(1)

式中e—感应电动势（单位：V）

N—绕组匝数

t—时间（单位：s）

Φ—磁通量（单位：Wb）

ψ—磁链（单位：Wb）

理想变压器就是按照法拉弟定律把加在输入绕组的电能通过磁场传递给输出绕组。

2.2理想变压器

原边和副边绕阻的匝比为1:n的简化变压器如图1所示。

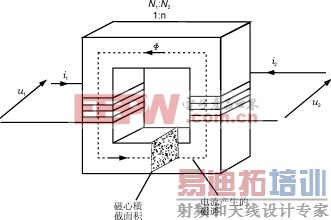
图1理想变压器

在变压器原边加一随时间变化的电压u1，它会产生一个流过原边绕组的电流i1。这个电流就会在磁心中产生一个磁通Φ，假设Φ全部通过磁心并全部通过副边绕组。则磁心中的磁通Φ就会在变压器副边绕组感应出一个电压u2和电流i2。

上述关系可用式（1）表示为：

u1=－N1dΦ/dt和u2=－N2dΦ/dt(2)

因此U1/U2=N1/N2=1/n

2.3磁通密度

在图1所示的理想变压器中，磁通Φ全部通过

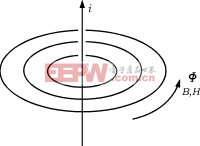
图2电流与磁场

磁心，如磁心的横截面积为A，则磁心内部的磁通密度定义为：

B=Φ/A(Wb/m2)(3)

2.4磁场强度

安培定律指出：(A)（4）

即在一个闭合磁路中，各段磁通路径长度li和相应磁场强度Hi乘积的总和等于施加的安匝数NI。

对于一个理想的磁路，即磁路中各点的磁场强度是一常数时，则NI=Hl，因此

H=NI/l(A/m)(5)

2.5材料的磁导率

磁感应强度（B）是磁场强度（H）的函数。它们之间的关系是：

B=μH（6）

式中μ—磁导率（单位：H/m）[p]

B—磁感应强度（单位：T）

H—磁场强度（单位：A/m）

在空气隙中的磁导率μ是一常数（μ=μO=4π×10－7

H/m）。其它材料B－H关系曲线的一般形式如图3所示。初始磁导率μi[1]是磁性材料磁化曲线始端磁导率的极限值，即：2.6B－H曲线

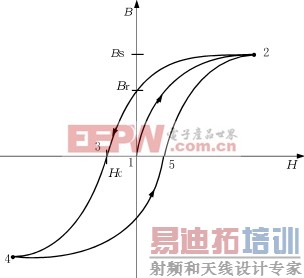
图3B－H曲线

图3展示的B－H曲线是一磁滞回线[2]，在B和H的增量很小范围内，磁导率μ可以认为是一常数。

如果导磁材料曲线起始部分磁场强度H值增加，则对应的B值就沿着曲线1→曲线2增加。在B和H是零的那一点曲线的斜率称为初始磁导率。当H值增加,到达点2以后，B值就不再随之增加。称此点为饱和点,它对应的B=BS。此时如减小H值，B和H关系曲线的轨迹变为2→3→4。当H减小到零时（2与3点之间），B有一剩余值，B=Br。当H反向后，B又逐渐减小，在点3，B值再次等于零，此时称为矫顽力,H=HC。反向H作用下的点4也是饱和点。如果此时H增加，对应曲线的轨迹是4→5→2。此时曲线不再通过1点。

在纯交流电的状态下，B－H曲线每一周期的轨迹都是2→3→4→5→2的环状曲线。

B－H曲线的磁滞回线与磁心损耗有联系，磁心损耗与磁滞回线环的面积成正比。

2.7相对磁导率

磁性材料的相对磁导率定义如下：

μr=μ/μo(7)

式中μr—材料的相对磁导率

μ—材料的绝对磁导率

μ0—真空磁导率[3]

2.8磁阻

根据图1理想变压器，应用式（4）可写出：

Ni=N1i1－N2i2和∑Hili=Hl=Bl/μ=lΦ/Aμ

磁阻Rm=l/Aμ(H－1)(8)

N1i1=ΦRm＋N2i2(9)

式（9）等式右边表示输出可得到的有效安匝数，要比等式左边的输入安匝数小ΦRm，这一项相当于在磁心内部建立起磁场所需的磁势，称它为磁心的励磁。

在理想情况下，当μ→∞Rm→0，则

i1/i2=N2/N1=n(10)

2.9自感

线圈的自感是线圈电流所产生的磁场在线圈上所形成的电感。它的定义如下：

e=－Ldi/dt(11)

式中L—自感（单位：H）

e—电感上电压（单位：V）

t—时间（单位：s）

各种几何形状电感的计算中，如包含有和安掊定律有关的H及I的求和/求积计算时，要求出它的电感量是比较复杂的。举一简单实例，求一环形磁心上理想

线圈的电感（见图4）。

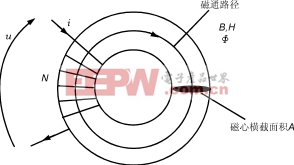
图4环形磁心上的电感

从法拉弟定律可得：

u=NdΦ/dt=NAdB/dt，于是

u=NAμdH/dt(12)

从安培定律可得：

Ni=Hl（13）

由式（12）和（13）可得：　　于是可求出电感为：

L=N2Aμ/l(14)

2.10互感

对于变压器和其它耦合线圈还应考虑副边（和其它）线圈对原边线圈所产生磁场的影响。两个线圈之间耦合磁通的影响所导致的电感称之为互感。

我们考虑两个线圈在同一个磁心上的情况。在一般情况下，不是所有磁通和所有线圈都耦合，如图5所示。

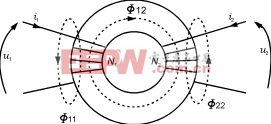
图5耦合线圈

按照安培定律可以写出：

Φ12=a(N1i1＋N2i2)

Φ11=bN1i1

Φ22=cN2i2[p]

式中a、b和c表示有效的比例常数。

按照法拉弟定律可以写出：

u1=N1d(Φ11＋Φ12)/dt

u2=N2d(Φ22＋Φ12)/dtu1=N12(a＋b)＋N1N2au2=N22(a＋c)＋N1N2a

又可以写出：

L1=N12（a＋b）—线圈1的自感

L2=N22(a＋c)—线圈2的自感

M=N1N2a—两个线圈之间的互感

在完全耦合的情况下Φ11=0、Φ22=0和b=0、c=0。因此，对于完全耦合的线圈可以认为：(15)

2.11耦合系数

耦合线圈在实际情况下，不是所有磁通都从耦合绕组的中间穿过。在2.10节中的常数b和c不再为零。表示线圈磁通耦合情况的另一种方法是用线圈的耦合系数k：M=k(16)

式中0≤k≤1

2.12同名端

简单变压器常规电路的同名端符号如图6所示。

每一绕组上方打的点是用来表示电感的同名端和绕组感应电动势的相位。当同名端和电流、电压的常规方向如图6所示时，则变压器的方程可写成下列形式：

u1=L1di/dt＋Mdi2/dt

u2=L2di2/dt＋Mdi1/dt

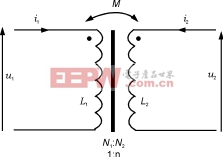
图6变压器电路的同名端

如果电压或电流的方向和图上标的相反时，则对

应项的符号也必需相反。

在通常的情况下，常规电压的方向是朝向“点”的方向，电流是通过“点”流进绕组。

2.13阻抗换算

当涉及变压器的电路分析时，通常都是把变压器副边阻抗换算成接在原边时的等效阻抗。这就是通常说的简化等效电路。

(1)并联阻抗换算

从视在功率S方面考虑可把阻抗改写如下：

S2=U22/Z2

从式（2）可得U1=U2/n，因而

S2=U12n2/Z2

所以跨接在变压器原边的等效阻抗是：Z1=Z2/n2，如图7所示。

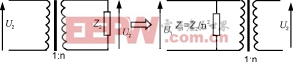
图7并联阻抗换算

(2)串联阻抗换算

从视在功率S方面考虑还可把阻抗改写如下：

S2=I22Z2，从式（10）可得i1=ni2，因而

S2=I21Z2/n2

所以跨接在变压器原边的等效阻抗是：Z1=Z2/n2，如图8所示。

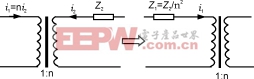
图8串联阻抗换算

2.14磁心气隙的影响

一个具有空气隙（为了清楚起见，图中的气隙是放大了的）的简单变压器的磁心如图9所示。磁心的等效磁通路径的长度是l，空气隙的长度是lg。

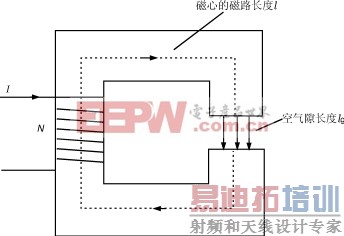
图9具有空气隙的磁心

假设气隙很小，则磁通和气隙界面垂直（没有边缘效应），并通过气隙保持连续，加上磁心材料内部的磁感应强度和界面是正交的，所以可写出下式：

B=μ0Hair=μ0μrHcore

所以Hair=μrHcore（17）

式中Hair—空气隙中的磁场强度

Hcore—磁心中的磁场强度

同样从安培定律可得：[p]