遗传模糊算法在短期负荷预测中的应用

提出了一种基于模糊逻辑原理的负荷预测方法，使用遗传算法对系统参数进行训练。在以往的模糊逻辑系统建立过程中,其主要参数（如模糊推理规则和隶属函数等）需要依靠运行人员经验或专家知识来确定，而本文利用遗传算法，通过对样本数据的自学习过程来获取系统参数。在遗传算法中，将推理规则与隶属函数参数的确定结合在一起，从而确定系统参数的最优组合，由此建立起一个较合理的模糊负荷预测系统。仿真实验结果表明，该方法能够达到满意的预测精度，具有良好的实用前景。
　　关键词：短期负荷预测；模糊逻辑系统；遗传算法

APPLICATION OF GENETIC-FUZZY ALGORITHM FOR SHORT TERM LOAD
FORECASTING OF POWER SYSTEM

Xiong Hao ；Luo Ri-cheng


(Electrical Engineering School ,Wuhan University, WuHan 430072, China)

　　ABSTRACT: A novel approach based on fuzzy logic system (FLS) is introduced to short term load forecasting (STLF).Traditional methods to choose membership functions and fuzzy control rules used to be done by means of integrating experience from experts in professional fields and technologic faculty. In this paper, however, a genetic algorithm based approach is developed to optimize parameters of membership functions and fuzzy control rules, simultaneously. And thus, the difficulties in building forecasting system, to some extent, can be disposed. At last, this new system is tested in an actual environment and produces superior results to traditional fuzzy logic short term load forecasting.
　　KEYWORDS: short term load forecasting; fuzzy logic system; genetic algorithm;


0 引言
　　 短期负荷预测是能量管理系统（EMS）的重要组成部分，也是确定机组组合、地区间功率输送方案和负荷调度方案不可或缺的重要一环。由于负荷变化与许多因素有关，且各种因素之间相互牵连，很难确定每一种因素对预测值到底有多大的影响，因此，应用经典数学方法难以清楚地描述问题的内部机制，问题变得更加复杂。
　　 早期的负荷预测主要是运用回归技术和时间序列法，但多为线性模型，不足以准确的描述电力系统负荷变化的非线性特性[1]。而近年来，人工神经网络（ANN）运用于负荷预测的思想备受青睐。该算法具有很强的鲁棒性、记忆能力、非线性映射能力以及强大的自学习能力，因而能够迅速地拟和出负荷变化曲线。然而却存在着收敛速度慢和容易陷入局部收敛等缺点，并且难以结合调度人员经验中存在的模糊知识，而这一模糊知识却又是极具价值的。
　　 模糊逻辑原理适合描述广泛存在的不确定性，同时具有强大的非线性映射能力。已经证明模糊逻辑系统可以作为通用的模糊逼近器以任意精度逼近一个非线性函数,并且能够从大量的数据中提取它们的相似性，这些特点正是进行短期负荷预测所需要的或是其他方法所欠缺的优势所在[2]。上世纪九十年代初，国内外许多学者已经开始探索模糊逻辑原理在电力系统负荷预测中的运用[2][3][4]，某些机构还将这一理论运用于实际系统[5]。然而，在众多的研究中，对于模糊推理规则和隶属函数的选取仍然依赖于专家知识和运行人员的经验，甚至在预测中需要运行人员参与其中[5]。这种建模方式需要工作人员对模糊系统的相关参数进行定期地离线修订，系统建立耗时费力，且更新缓慢。本文结合模糊数学理论和短期负荷预测研究的最新成果，利用在求解组合优化问题中具有优良特性的遗传算法来确定模糊逻辑系统的相关参数，从而较为迅速地构建出一套基于模糊逻辑原理的负荷预测系统。以期进一步挖掘模糊逻辑系统在负荷预测应用中的强大生命力。

1 遗传算法在模糊逻辑系统中的应用
　　 一般来说，模糊逻辑系统的设计中最棘手的问题主要是以下两个：其一为隶属函数个数、形状的确定及其坐标位置的调节；其二是模糊规则的确定，如果在推理句式已经固定的情况下，该问题又可细化为对各个模糊条件语句推理结果（后件模糊词）的选取。两部分内容互为依赖，相辅相成。已经有许多学者提出了许多有益的思想对这两问题分别进行改进，然而由于隶属函数与模糊规则具有高度的依赖性，最优模糊逻辑系统的建立取决于两方面的有机结合，孤立地研究单方面因素的优化往往只能得出问题的次优解，难以在全局上把握问题的实质。事实上，隶属函数参数的调节与模糊推理语句中待定模糊词的选取可以看作是一个多参数组合优化问题。而遗传算法非常适合于解决组合优化问题，它具有隐含的并行特性和全局搜索能力，可以很好地对隶属函数和模糊规则进行综合寻优。
　　设样本集合的输入量为X={x1,x2,…,xN},其中xj(j=1,2,…,N}为n维输入向量，样本集合的输出量为Y={y1,y2,…,yN},样本集合的输入X对应的模糊逻辑系统的输出为

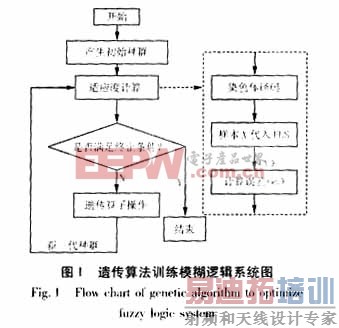
图1表示了基于遗传算法的模糊逻辑系统的训练过程。设种群规模为K，每一次迭代所产生的染色体为lj(j=1,2,...K)。在适应度计算模块中，首先对每次新产生得染色体lj进行解码，还原成其所确定的模糊逻辑系统Lj。然后将样本集合的输入
集合的输出量Y进行统计处理，抽取误差平方和作为分析指标，即染色体lj对应的统计量作为其目标函数，如式（1）：
　
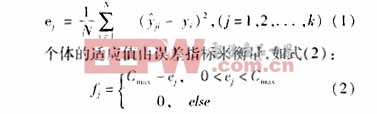
　　其中，Cmax为一给定值。选取f*为系统的最优适应值，当循环迭代出现期望的适应值fo(fo≥f*)时，迭代终止，由此确定最优模糊逻辑系统。

2 模糊负荷预测系统的参数选取
　　该系统的工作过程分为两个阶段：训练阶段和预测阶段。训练阶段是将已知的历史负荷资料作为评价指标，利用遗传算法对模糊逻辑系统的参数进行选择，这一阶段可以看作是一个对人类经验（备选解群）进行计算机总结进而寻找出最优模糊逻辑系统的过程。预测阶段即系统的实际应用阶段，将预测日的相关因素输入预测系统，得出预测结果。
　　 本文设计的模糊负荷预测系统共分为24个独立的小系统，每个小系统针对24个不同的时刻，对样本数据分区处理。而在对预测日负荷进行集中预测。

[p]

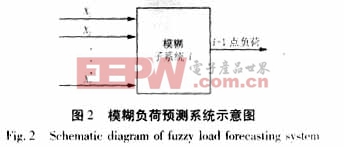
图2所示的结构为小系统i的输入输出关系。模糊关系用Mamdani最小规则定义，合成算法使用“∧－∨”运算准则，解模糊转换采用重心法（亦称为加权平均法）。输入变量X的选取一般考虑的因素为：日期类型、天气状况(气温、降雨量、湿度和风速等)、负荷近期变化趋势等一些因素。根据区域性和季节性对负荷变化影响的差异，不同的系统可以选取不同的输入量。通过研究预测地区的负荷特性在近几年的变化情况，本文选取输入量X有三(即图2中的n=3)：X1为周日期类型；X2为预测日时刻T的气温；X3为近期负荷变化趋势。具体的定义见2.1节。
2.1系统输入量及其隶属函数的选取
　　输入量X1为预测日的日期类型。根据负荷的周循环特性，模糊词集定义为T（A1）={周一，周二，周三，周四，周五，周六，周日}。显然，该词集中的各元素之间不存在模糊关系。为适应模糊逻辑系统运行，需要将其按照模糊数学形式处理，即定义

　　这一变量的隶属函数参数实际上已经确定，因此不参与随后的遗传算法的寻优过程。
　　输入量X2为预测日T时刻的气温预报。该变量为影响负荷预测的主要因素，且与负荷变化成非线性关系，按照隶属函数的选取原则[7]，将模糊词集划分为T(A2)={NB(负大),NS(负小),ZE(中),PS(正小),PB(正大)}，经过反复的试验，本文对上述的词集依次选取梯形(偏小型)，三角形、梯形（偏大型）三种形式。

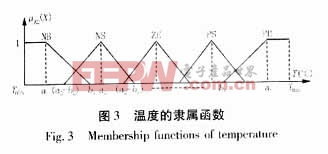
如图3所示，温度隶属函数中所需调节的参数为a1、b1、a2、b2、a3、b3、a4、b4、a5、b5等十个参数。每个参数对应的调节范围是[Umin，Umax]。值得注意的是，论域UT=[Tmin,Tmax]的选取可按照季节的不同进行设定，以期提高预测的精确度。
　　输入量X3为预测日前三周相应日0时刻负荷量的加权平均值。它反映了负荷的近期变化趋势。结合文献[6]中的平均值求法，给出如公式（4）:
　
　　其中α＋β＋γ＝1，α≥β≥γ。该量代表过去3周同类型日同一时刻T的负荷的加权平均值。如果过去3周同类型日中的某一天正好是节日，则取再前一周的数据，并根据α、β、γ的调节确定近期与远期历史数据对当前的影响。这一输入中包含负荷的动态信息和近期的发展趋势，对于预测的准确性是至关重要的。
　　其隶属函数的确定方式与输入量X2相似，但因该变量与预测负荷基本成线性关系，因此选取的隶属函数个数较少，选定三个模糊词，即T(A3)={NB(低),ZE(中),PB(高)}。
　　同理，输出量Y分为4档，设定模糊词集T(B)={NB(负大),NS(负小),PS(正小) ,PB(正大)}。
2.2 推理规则的选取
　　 推理规则由一系列多维多重模糊条件语句组成，本文中输入量有三个，因此是三维多重模糊条件语句，其基本形式为“IFx1 is Ali and x2 is A2j and x3 is A3k THEN y=Bm”。其中i、j、k分别为各输入量的隶属函数个数，m为输出量隶属函数的个数。由此可知本文系统可能的规则数为7×3×5＝105个，对105个模糊条件语句的确定实际上是对每一条语句选择合适的Bm。

3 遗传算法应用中的问题
　　编码方式的优劣决定了遗传算法总体效果的优劣，它直接影响着遗传算法的搜索能力和保持种群稳定性。如果编码不适当，会使得不可行解过多，搜索可行解困难重重，往往需要加上大量的前期或后期补救措施才能够完成计算。因此，如何制定优良的编码策略是绝大部分遗传算法问题中的重要问题。对几种编码进行分析比较后，本系统选用二进制编码方式，每三位基因串表示隶属函数的一个参数；使用两位基因表示每条推理条件句的推理结果，然后将两个基因串连接起来，形成表征模糊逻辑系统的染色体。
　　对于表示隶属函数的基因串部分，假设某一参数ai(或者bi)的取值范围是[Umin，Umax]，用一l位数来表示，其关系表示如下： u=Umin+(n/(2t-1))(Umax-Umin)。本文中l=3。正如第二节中所述，该系统输入量X2有5个隶属函数，输入量X3共有3隶属函数，输出量Y为4个隶属函数，每个隶属函数的待定参数为两个，于是基因串共长72位，形如下式：

[p]

从第73位开始至282位是对105条模糊条件语句的编码，每两位基因对应一条语句，例如如果X73X74若为“01”，则表示相应的模糊条件语句为“IF x1(日期类型)is A11（周一），and x2(T时刻气温)is A21(很低)and x3(近期负荷量趋势)is A31(底)then y(预测量)is B1 (很低)”。
　　在确定的编码方式后，遗传算法对种群中的染色体进行各种遗传算子操作（选择、交叉和变异等），应当采用各种改进措施以提高算法的搜索效率，避免早熟收敛等问题。

4 负荷预测仿真分析
　　为检测系统的可行性，针对所开发的系统进行计算机仿真。本文利用河南省某市2002和2003年夏季（4、5月份）负荷资料，对2003年5月份第三周星期一的日负荷进行模拟预测。
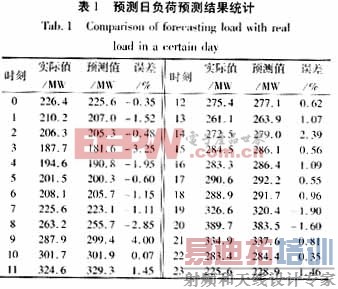
　　首先将两年中4、5月份负荷资料和天气资料按照24个不同时刻分成24份，然后选择出可以作为训练样本的数据来。此处我们选择了40份有效历史数据，按照第2、3节所叙述的方法对系统参数进行训练。最后对选定日进行日模拟负荷预测。表1给出了实际值，预测值和误差的记录。

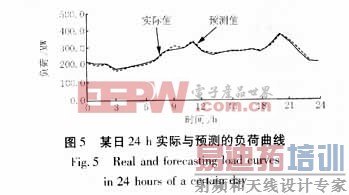
5 结束语
　　电力系统短期负荷预测一项极为复杂的工作。由于负荷的变化要受到诸多因素的影响，而这种影响往往又难以用经典数学方法准确地加以描述，所以往往很难达到预期的预测效果。本文利用遗传算法对模糊系统中的隶属函数和推理规则进行训练，并将由该方法所确定的模糊逻辑预测系统应用于短期负荷预测。对影响负荷变化的因素进行研究，结合具体的问题，选取了适应于系统的输入量。在遗传编码方面，将确定隶属函数与推理规则的各种参数进行统一编码，以求得系统参数的最优组合。实验结果证明了该方法具有良好的预测性能，和较好的发展前景。