DC－DC开关变换器中混沌现象的研究综述

1 引言
　　从非线性动力学角度来说，开关变换器是一个强非线性时变动力学系统，因此存在着丰富的非线性现象，包括各种类型的次谐波、分叉与混沌等。由于混沌动态是一种不稳定振动，混沌现象是一种不正常不可靠的现象，混沌的不确定性将导致系统的运行状态无法预测，从而使变换器的控制性能受到极大的影响，甚至完全不能工作，所以研究开关变换器中混沌产生的方式、分析方法有助于我们在设计中避开这种不理想现象，使变换器工作于稳定的周期，这对于正确设计和调试开关变换器具有重要的指导意义。
　　本文对混沌的国内外研究现状作一综述，并详细介绍其分析方法。

2 混沌的基本概念
　　1963年，Lorenz从简化的大气模型中推导出著名的Lorenz方程，这组三阶的微分方程呈现出一种奇异的现象，即混沌现象，从此揭开了混沌学发展的新篇章。Lorenz微分方程组如下：

(1)

　　在这个系统中，S ，R，B是可变参数，其中任意参数的改变都可能导致系统从周期态向混沌态的转变[1]。
　　从Lorenz系统中研究可知，产生混沌的原因是耗散和非耗散相互作用的结果。耗散作用的整体稳定性和非线性作用的局部不稳定性作用便形成了混沌[2].而奇异吸引子是混沌的本质所在。这时候人们发现即使对于典型的可用确定论方法描述的系统来说，只要该系统稍微复杂一些，在一定条件下也会产生非周期的表面上看起来毫无规律的运动，改变了那种认为用确定论方法描述的运动都属于规则运动的错误观念。这种来自可用确定论方法描述的系统中的无规则运动，称为混沌或内在随机性。它表面上是随机运动，实际上是有一定结构的形式，而真正的随机行为出现在嘈杂系统中。混沌运动通常还具有确定性运动所没有的特征，如局部不稳定而整体稳定、无限自相似、对初值变化的高度敏感性、奇异吸引子中包含多个不稳定周期轨道、连续的功率谱等[3]。首次证明开关变换器中存在混沌的是Brockett和Wood，他们在1984年发表的一篇会议论文中指出受控的Buck 变换器可产生混沌行为[4]。1988年，Hamill和Jefferies首先对开关变换器中的混沌现象进行了理论分析[5]。而文献[6]指出由于开关变换器是强非线性离散系统，而非线性微分方程的解不是唯一的，当非线性系统的周期解处于临界状态时，它对微小的参数摄动或初始条件变化都极为敏感，就可能进入连续分频状态，最后出现混沌。

3 混沌的分析方法
　　Middlebrook等在1976年提出的状态空间平均法[7]是目前使用最广泛的方法。它将时变电路变成了非时变线性电路，从而可求稳态工作点、小信号传递函数等。它是简明性和准确性的一个较好的折中。但也存在着稳定性分析不准确、不能分析纹波、无法分析准谐振变换器等缺点。另外，它在连续导电模式中忽略了开关变换器频率的影响，由此而产生的线性模型中，占空比成为连续的时间变量，然而实际上占空比是定义成离散时间变量的，在一个开关周期内讨论占空比的变化是毫无意义的[8].由于所得到的是一个线性模型，忽略了开关变换器的非线性特征，因此不可能对开关变换器中的次谐波、混沌等非线性现象作出正确的分析，这些不足使得离散时间模型[9]应运而生。它保留了变换器的非线性特性，是较为准确的一种方法，一般可以得到映射的隐式表达。它的主要特点是提出采样序列的概念，而不是把开关描述成连续的，即每隔一定时间对变换器作一次采样，通常是在波峰波谷处采样更方便。开关周期内状态的变化由一映射函数描述。这个函数可能会较复杂，但一旦得到，就可以用计算机来对它进行反复迭代，从而确定变换器的状态是怎样从一个周期演变到另一个周期的。

　　文献[10]是基于离散时间模型的非线性迭代映射法。一般的，其状态方程可以描述为=f（x，t），其中x是n维状态矢量（常为电容电流或电感电压），每一个周期对X采样（通常在波峰或波谷处），即可得到一个离散系统。于是就得到一个{ }序列，时间就不出现在方程里了。

3.1 一维映射
　　对于一维映射 x——>F（x）， F是一个作用在一个实数上来产生另一个实数的函数。满足方程x*=F（x*）且在映射下保持不变的点叫F的固定点。我们的兴趣在于用这个函数将一个区域划到它自己内部。例如x—>ax（1-x）， 其中a是一个参数，0≤a≤4，这个函数就是将区间[0，1]划到它内部。若a=2，则方程变为
m=0，1，2
这是一个一阶差分方程，x的当前值仅由前一个值决定。从任一个初值开始反复迭代就可以得到一个序列{ }.任选一个不等零的初值，序列最终收敛于x*=0.5，这个点叫做吸引性固定点。反之对于固定点x*=0，若初值不等零，而序列会偏离初值，则这个点不具有吸引性。 由上可知，固定点对系统有着重要影响。 特别的，稳定行为与吸引性固定点有关系。，那样的点叫稳定固定点。而不具有吸引性的固定点会导致混沌。

3.2 高维映射
　　迭代法对高维映射也适用。在n维情况下，令人关注的是n维矢量之间的关系。这时候，F作用在一个矢量上以产生另一个n维矢量。与一维映射同样，我们的兴趣在于把一个区域划到它内部，不同的是这个区域是一个n维空间.下面给一个二维例子,

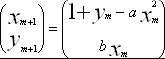(2)

其中x=
, a、b均是参数。因为必须把函数画在二维空间里,所以要看高维映射是较困难的,甚至n =2这种情况也不例外。同样，对于高维映射，满足
的矢量即为固定点。如当 a=1.4、b=0.3时,方程(2)有两个固定点,但都不具有吸引性,因而会导致混沌。

3.3 数值仿真法
　　数字仿真是指利用各种各样的算法以求得变换器某些特性数字解的方法。它分为直接数字仿真法和间接数字仿真法两种。数字仿真的优点是准确度和精确度都高，可以得到响应的完整波形；适用范围广，可进行小信号分析和大信号分析。

　　由于混沌动力学系统的复杂性，很多混沌动力学系统不能用已知函数表示其通解，使得解析法很多时候无能为力，而且用解析法建模时，常常需要作出某些近似，以简化分析。众所周知，开关调压系统存在着功率级电路的开关非线性和控制电路中脉冲调制器的饱和非线性，因此不能用精确方法设计电路，也难以用解析法对混沌类现象进行有效的预测，同时这类系统受到的扰动常常是大幅度的，这时系统在大信号扰动下工作，对于大信号分析，一般很难用解析法求解，更需要借助于数字仿真，从而这就使通过数值计算来描述混沌行为的演化过程对开关变换器的混沌进行数值模拟显得十分重要[11]。
　　下面以PWM型BUCK变换器为例，用PSPICE对其进行仿真。如图，假定电路中的器件均是理想的，电路中参考电压Vref输入至反相器的反相端，R上的电压V（t）输入至误差放大器OA1的正向输入端，OA2的正向端为一个时钟信号——锯齿波电压，放大器产生一个控制信号，作用于PWM，与时钟信号比较。每周期初始，ＰＷＭ输出脉冲，当反馈电路的输出端（即控制电压）高于锯齿波电压时，输出为高电平，压控开关导通；当锯齿波电压上升到控制电压时，输出脉冲截止。直到下一周期开始，再次输出脉冲。因此控制电压的波形决定了输出脉冲的宽度，进而决定了开关管的导通时间。这样产生一系列的脉冲信号来控制主电路的压控开关的。电路中的参数值如下： 输入电压Vs=10v ，电容C=100uf，电感L=100uh，负载电阻R=22， 参考电压Vref=5v，锯齿波电压Vpulse（0v，10v，0s，199.99u，0.005u，0.005u，200u），放大器的放大倍数e=15，稳态时，变换器的输出含周期性的纹波，然而某些情况下，电路会发生多脉冲现象，开关通断多次，从而增加了开关损耗，变换器的效率降低。我们用PSPICE仿真后可得，如下图：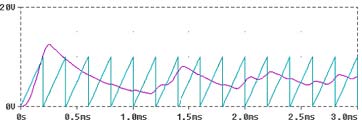

4 稳定性及稳定条件
　　一般的，稳定的DC—DC变换器表现为周期性的稳态。一旦初始暂态值衰减，状态变量就以周期重复。控制相应的离散系统的映射有一个吸引性固定点：在周期性的稳态，每一个周期都与下一个相同，所以在每个周期采样得到的情况都一样。若变换器是局部渐近稳定，相应的一个小的扰动它会使周期稳定下来，这个离散系统相应的序列会收敛于这个固定点，因此，这个点是吸引子。相反，若变换器初态是不稳定的，这个序列会偏离固定点。因此，可以得出结论：映射的固定点的稳定性决定连续系统的局部稳定性。一个吸引性的固定点对应着连续系统的周期性的稳态。

　　一阶系统稳定的条件是映射在固定点处的梯度在-1和1之间。 即

　　固定点的稳定性也可以推广到高阶。不同的是，一阶的稳定性由梯度决定，而高阶由特征增益率决定，固定点的特征增益率是映射在固定点处的雅可比阵的n个特征值。其中雅可比阵是对各个元素求X偏导后所得矩阵。高阶系统稳定的条件是若特征增益率都落在复平面上的单位圆之内，则固定点稳定。

5 混沌的研究状况
　　因为分叉、混沌等不稳定现象与系统的非线性密切相关，所以在分析研究时必须跳出线性电路的范畴[12].目前最常用的方法是一维映射法。一般的，开关变换器的离散表达式可写作，其中为输入,是第N个周期的占空比, F、T分别是系数矩阵的指数函数。对于闭环工作的开关变换器，一般有
，是非线性函数，因而
    ，这就是一维映射法的原理[13].现在已有比较成熟的理论。文献[10，5，14]使用该法分析了电流反馈的变换器的分叉混沌现象。最近，Tse的一系列工作如[15]都是推导出该一维映射的解析表达式，通过研究这一映射来得到变换器的动力学性质，揭示了变换器从倍周期、分叉走向混沌的具体过程。

  　另外，从国内外的研究工作来看，各种频繁出现在其他领域的线性或非线性现象，都可以在开关变换器中找到类似情况。开关变换器中的混沌运动同样也与周期轨道有密切关系，在分叉参量变化过程中，闭环系统的变换器往往先以各种方式经历一系列周期、倍周器、准周期事件，最后才进入混沌状态，这通常称为通向混沌的具体道路。文献[6]从计算机模拟和实验两方面验证了开关变换器不仅在PWM闭环时会产生混沌，即使在开环情况下，由于二极管和晶体管等开关功率元件的非线性极间电容影响，变换器仍可能产生混沌。文献[16]研究了电流控制型变换器中的输入电压，电容电感以及开关频率等参数对系统分叉、次谐波、混沌等不稳定行为的影响，并画出了稳定区域和不稳定区域。目前，不稳定的分析方法还不完善。文献[17]用微分动力系统方法研究了Boost变换器的分叉现象，认为该电路存在静态分叉和动态分叉并得出其存在的条件。虽然文献[17]的方法处理严格，结果较为准确，但是较繁琐。

  6 结束语
    　本文对变换器的混沌概念、特点、分析方法、研究现状作了一个较全面的综述。由上可知，随着混沌理论的发展，变换器中的混沌现象的研究也有了一定的成果。，混沌的分析方法还主要是一维映射法，但是一维映射法是否适合于所有的变换器，是否还有别的方法，这都有待进一步研究。

    参考文献
    [1]伊奕光 刘文波 于盛林 功率电子电路中的混沌现象 南京理工大学学报
    [2]李饶亭 蔡诗东 混沌和李雅普诺夫特征指数 1996，25 （5）：282~286
    [3]周宇飞 丘水生 高频开关电源的混沌现象及其应用研究动态 电源世界2001年第10期
    [4]R.W.Brockett and J.R.Wood， Understanding Powee Converters Chaotic Behavior Mechanisms in Proctive and Abnormal Modes Proc.Powercon 11，paper E-4，1984
    [5]D.C.Hamill and D.J.Jefferies， Subharmonics and chaos in a controlled switched – mode power converter IEEE Trans .Circuit Syst，。Vol .CAS-35，no 8，pp.1059- 1061，Aug.1988.
    [6]张鸿 刘嘉勇 开关功率变换器中的混沌现象研究 成都科技大学学报 Vol 90 ，No 2，1996
    [7]R.D.Middle brook and S. Cuk， A general unfied approach to moddeling switching—converters power stage IEEE PESC Rec 1976 ，pp.18——34
    [8]刘健 开关电容功率变换器 陕西科学技术出版社 1998年6月
    [9]G.C. Verghese. M.E.Elbuluk，and J.G，Kassakian， A general approach to sampled-data modeling for power electronic circuits IEEE Trans， Power Electron， vol. PE-1，no，2 pp，76—89，Apr，1986
    [10]JONAAAATHAN H.B. Deane and David C. Hamill ， Member. IEEE Instability ，Subharmonics and Chaos in power Electronics Systems
    [11]刘健，陈治明，钟彦儒 多路独立输出的继承谐振DC—DC变换器及其计算机仿真 微电子学与计算机 Vol.13，No.3，1996，pp.31-34
    [12]林波涛 丘水生 DC—DC开关变换器分析方法综述 电路与系统学报vol 3，no 3， 1998 年8月
    [13]郝柏林 从抛物线谈起一混沌动力学引论 上海：上海科技教育出版社 1993
    [14]J.Deane and D，Jeffries，"Insteability，subharmonics and chaos in power electronic systems" IEEE Trans .on Power Electronic，Vol.5，No.3，1990，pp.260~268
    [15]C.K.Tse， Flip Bifurcation and chaos in three in three state boost switching regulators IEEE Trans on Circ and syst.I Fundamental theory and application，Vol 41，no 1，1994，pp.16~23
    [16]Krishnendu Chakrabarty， Goutam Poddar， and Soumitro Banerjee Bifurcation Behavior of the Buck Converter IEEE Trans on Power Electronics Vol 11，No 3 1996
    [17]F.Tan and R.Ramshaw， Instability of a Boost converter system under large parameter variations IEEE PESC Rec，1989，pp，138~143