- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
数字控制式LLC谐振变换器建模分析与验证
录入:edatop.com 点击:
摘要:针对半桥LLC谐振变换器的建模及其验证展开分析,同时分析了数字控制对系统稳定性造成的影响,并给出采用数字控制时系统稳定性的解决方案。首先,通过扩展函数描述法得到传统的模拟域数学模型,并在Saber中搭建仿真模型,利用小信号分析法验证该数学模型的准确性,从而得出得到的系统数学模型具有参考性,由此提供了环路设计的基础;其次,采用数字控制,考虑到其离散特性,分析了数字控制对系统稳定性的影响,并通过Matlab仿真验证了该理论的正确性,最终设计出性能良好的数字PID补偿器;最后,针对实际应用场合,搭建实验平台,进行相关实验验证。
前言
现今蓄电池充电器常用的充电拓扑有正激、Buck、Boost以及各种形式的谐振变换器,而谐振变换器凭借其软开关特性得到更加广泛的应用,其中半桥LLC谐振变换器结构简单,允许空载运行并具有较宽的输入电压范围,且通过磁集成技术可以提高整机的功率密度,具有明显的优势,因此文中选用半桥式LLC谐振变换器作为研究对象。此外,由于数字控制具有元器件少、控制灵活、容易实现复杂控制算法优点,所以文中选用数字控制。
蓄电池充电器主要工作于恒流或恒压输出模式,要求变换器具有良好的稳态跟踪性能,并且考虑到蓄电池在充电过程中,其所需要的充电电流会不断变化,即蓄电池负载并非始终保持恒定,此要求变换器具有较好的动态性能,能够较快跟踪到参考电流变化,而现在市场上的变换器不具备以上特性,所以需要对变换器的控制环路进行设计优化。首先采用扩展函数描述法[1]对其进行建模,得到开环数学模型,并验证该模型的准确性;其次,分析数字控制带来的计算延时、控制延时对传统数学模型稳定性的影响,并给出相应的解决方案并设计数字PID补偿器;最后根据实际应用参数,进行仿真和实验验证。
1 系统环路设计
1.1 扩展函数描述法建模
由于谐振变换器的谐振特性,其状态变量中含有许多开关频率处的信息,传统的状态空间平均法不再适用,因此采用扩展函数描述法(EDF)建立半桥LLC谐振变换器的数学模型。如图1所示为半桥式LLC谐振变换器原理图。

首先,选择激磁电感电流、谐振电感电流以及谐振电容电压作为状态变量,并根据拓扑结构,列写非线性时变状态方程:

(1)
式(1)中:Lr为谐振电感,Lm为激磁电感、Cr1、Cr2为谐振电容。
其次,根据Fourier分解[2]将周期信号分解为正弦函数之和,只考虑基波分量,得到所需的近似大信号模型,系统稳态运行后,变量不随时间变化而变化,因此忽略模型中的时变分量,即可得到稳态工作点求解方程并转化成矩阵形式,最后在稳态工作点附近,进行变量分离,获取系统的小信号数学模型,并表示成矩阵形式。

(2)
其中,
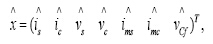


通过以上过程可以得到输出电压对开关频率的关系矩阵:
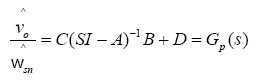
(3)
为进行环路设计,首先需要验证上述方法得到的数学模型的准确性,如表1所示为实际系统参数。

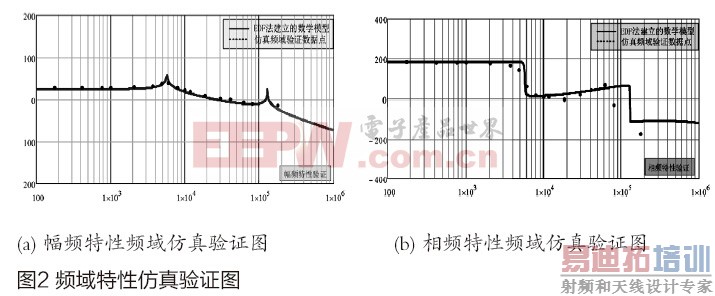
在Saber中搭建仿真模型,逐点仿真。仿真验证结果如图2所示。
为了获得良好的系统动态和稳态特性,需加入补偿环节,因考虑系统的寄生参数[2]后,系统阶数较高,因此在设计补偿环路时,通过加入适当的零极点,来改善系统的频域特性。本文采用PID控制器[3],为实现零极点对消,将PID控制的表达式表示成:
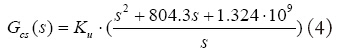
通过调节系数Ku使得系统获较好的低频增益和穿越频率点。如图3所示为补偿前后系统的幅频、相频增益特性曲线。
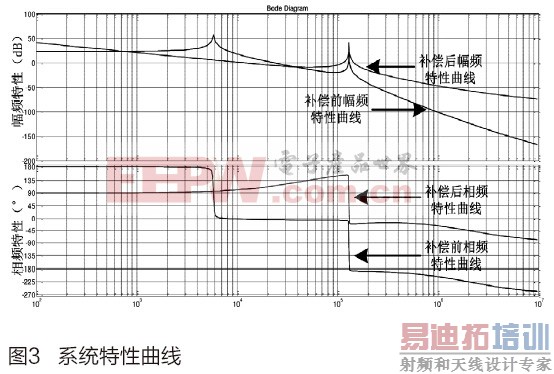
对比补偿前后系统频域特性,经过补偿的系统特性明显得到了改善,穿越频率[4]在11.8kHz处,相位裕度约为87.5o,符合模拟域的环路设计要求。
1.2 数字控制对环路稳定性的影响
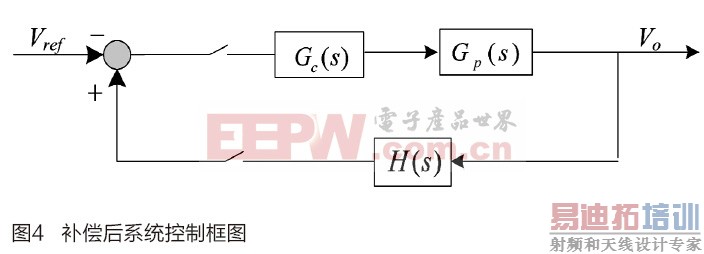
由于数字控制的离散特性,须将所设计的模拟PID控制器在z域下进行稳定性的判定。作为理想的PID控制器,须满足以下条件:一是补偿后控制系统在z域稳定;二是控制器具有可实现性,本节主要通过z变换实现最优PID参数的整定[5]。加入补偿器后时域控制框图如图4所示。
分别对功率级传递函数Gp(s)、补偿器传递函数Gc(s)进行z变换,得到其z域的闭环特征方程:
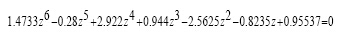
(5)
从而得到补偿后的系统z域闭环零极点分布图,如图5所示。
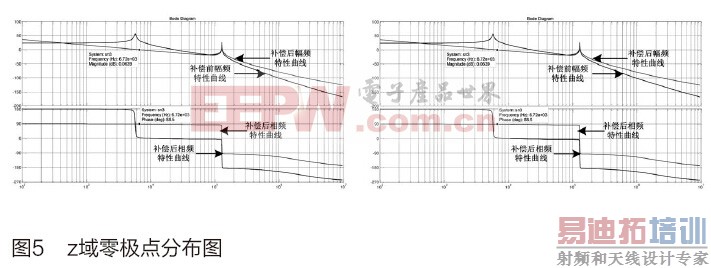
根据z域稳定性条件[6]:闭环传递函数的极点应位于单位圆内。可以看出,此时在数字离散域中系统是不稳定的,因此必须选用适合于数字控制的PID控制器设计方法。
与传统的模拟控制器相比,数字控制器由于DSP等数字器件的固有特性,需要在设计时进行相关的考虑。数字控制核心DSP采样输出电压获得反馈信号,经过补偿器控制后作为调制信号[7],从而控制输出电压恒定,由此可知,更新驱动脉冲的调制信号与实际采样信号之间存在一个周期的延时,这可以通过加入零阶保持器来模拟。并且由于理想采样开关的存在,使得控制器具有1/Ts的增益特性[8],因此可以得到数字PWM在连续时域设计时的等效模型。
由上面的介绍可知,与数字PWM相关的延时效应可以通过加入ZOH来等效,实际上,采用数字控制器时,还存在另外一种延时效应,即控制算法的计算延时[3],这是由处理器从采样到输出一个新的调制量所需要的计算时间决定的,通常假设该控制延时时间为一个调制周期,即Ts,将此延时加入在模拟控制器设计中,可以通过加入延时环节
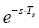
来等效,从而得到以下表达式来模拟数字控制带来的影响。
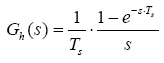
(6)
通过以上分析,本文以z域稳定性作为设计前提,通过降低系统带宽解决控制器计算延时等带来的问题,设计穿越频率为
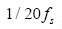
,即开关频率的二十分之一处,保证有足够的相位裕度。考虑数字影响后,系统开环传递函数[9]为:

(7)
将
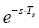
用有理函数之和来等效,得到等效后开环传递函数:

(8)
得到补偿后的开环传递函数:
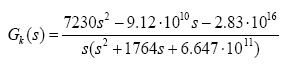
(9)
在Matlab中绘制补偿前后系统开环传递函数的Bode图,如图6所示。
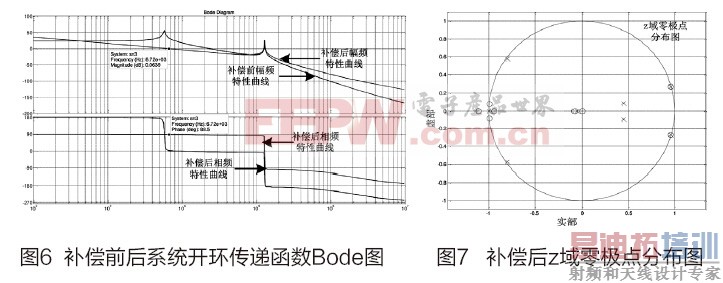
如图6,补偿后系统的开环穿越频率为6.72kHz,相位为88.5°,满足设计要求。同样地,仍需对所设计数字补偿器进行离散域稳定性的验证,对补偿前开环传递函数Gpd(s)以及PID控制器Gcd(s)进行z变换,并乘以
得到z域传递函数。据此绘制其零极点分布图如图7所示。
从图7可以看出,经过重新设计后的PID控制器满足离散控制要求,所设计的系统是稳定的。
2 仿真与实验结果
通过以上分析,得到了相应的PID补偿器,本节以电流闭环为例给出了相应的仿真结果。
2.1 仿真结果
图8所示分别为变换器恒流输出模式下负载突卸、突加的仿真波形。
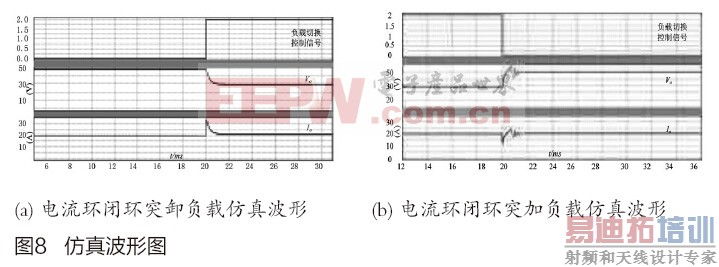
从仿真波形上可以看出,电流环跟踪性能良好,能够按照指定准确输出,并且动态过程没有过大的冲击,表明本文所设计的环路具有良好的稳态和动态性能。
2.2 实验结果
按照实际系统结构,搭建实验平台,平台包括电源侧、变换器侧以及负载侧,其中电源采用单相调压器进行模拟,调压器额定频率50Hz工频,交流输入220V,输出电压可调范围为0~250V;变换器为由LLC谐波变换器、EMI滤波器、控制芯片等构成的控制平台,其中半桥LLC谐波变换器功率变压器采用EE55磁芯,原副边绕线匝数分别为6、3,变比为2;负载侧由电子负载模拟蓄电池,设备可以作为恒压负载或恒流负载使用,从而模拟蓄电池的恒压充电以及恒流充电特性。
图9为变换器运行于恒流模式,指定输出30A、10A的稳态实验波形以及负载突加、突降时的动态响应实验波形,用以验证本文所设计的数字PID控制器的闭环控制性能。
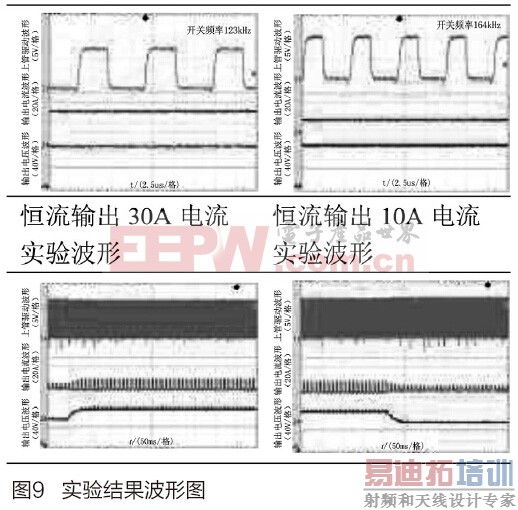
从图9可以看出,本文所设计的变换器能够按照指定电流进行输出,且稳态性能良好,针对蓄电池负载,变换器可以实时地根据负载情况进行动态跟踪,达到蓄电池充电的目的。
从实验波形上可以看出,实验结果与仿真结果具有较好的一致性,验证了环路的稳态跟踪性能以及动态响应特性。
3 结论
通过扩展函数描述法得到数学模型,给谐振型变换器的建模提供了理论支撑;再通过离散化,在z域验证数字控制式系统的稳定性,证实了数字控制延时等对系统稳定性的影响,最后,根据仿真和实验结果可以看出,本文所设计的系统环路具有良好的稳态跟踪性能和动态响应特性。在此基础上,可以展开进一步研究,寻求除降低系统带宽外更准确的适用于数字控制的环路设计方案,综上所述,本文具有较高的研究和参考价值。
参考文献:
[1]石艳敏. 电动汽车车载智能充电器的研究[D]. 南京:南京理工大学. 2011
[2]Bo Yang.Topology Investigation for Front End DC-DC Power Conversion for Distributed Power System.Virginia Polytechnic Institute and State University.2003
[3]徐建明. PID控制器及其设计方法研究[D].浙江:浙江工业大学. 2002
[4]Simone Buso, Paolo Mattavelli. Digital Control in Power Electronics. 2006
[5]肖献保,冯根生.铅酸蓄电池快速充电技术研究[J].重庆科技学院学报自然科学版,2010,12(4):134-135
[6]周震宇, 张军明, 钱照明. 基于PIC单片机的数字式智能铅酸电池充电器的设计[J]. 电源技术应用,2006,9:18-21
[7]张治国, 谢运祥.LCC谐振变换器的电路特性分析[J].电工技术学报,2013,28(4):50-56
[8]Yanyan Jin,Jianping Xu,Guohua Zhou,etal. Small Signal Modeling of Digital V2 Control for Buck Converter with Pulse Frequency Modulation[J]. IEEE,2010,2(12):102-105
[9]Agasthya Ayachit,Dakshina Murthy-Bellur.Steady-State Analysis of Series Resonant Converter Using Extended Describing Function Method[J]. IEEE,2012,12:1160-1163
[10]Yongsuk Choi, Heungjun Jeon, Yong-Bin Kim. A Switched-Capacitor DC-DC Converter Using Delta-Sigma Digital Pulse Frequency Modulation Control Method[J]. IEEE,2013,66(8):356-359
前言
现今蓄电池充电器常用的充电拓扑有正激、Buck、Boost以及各种形式的谐振变换器,而谐振变换器凭借其软开关特性得到更加广泛的应用,其中半桥LLC谐振变换器结构简单,允许空载运行并具有较宽的输入电压范围,且通过磁集成技术可以提高整机的功率密度,具有明显的优势,因此文中选用半桥式LLC谐振变换器作为研究对象。此外,由于数字控制具有元器件少、控制灵活、容易实现复杂控制算法优点,所以文中选用数字控制。
蓄电池充电器主要工作于恒流或恒压输出模式,要求变换器具有良好的稳态跟踪性能,并且考虑到蓄电池在充电过程中,其所需要的充电电流会不断变化,即蓄电池负载并非始终保持恒定,此要求变换器具有较好的动态性能,能够较快跟踪到参考电流变化,而现在市场上的变换器不具备以上特性,所以需要对变换器的控制环路进行设计优化。首先采用扩展函数描述法[1]对其进行建模,得到开环数学模型,并验证该模型的准确性;其次,分析数字控制带来的计算延时、控制延时对传统数学模型稳定性的影响,并给出相应的解决方案并设计数字PID补偿器;最后根据实际应用参数,进行仿真和实验验证。
1 系统环路设计
1.1 扩展函数描述法建模
由于谐振变换器的谐振特性,其状态变量中含有许多开关频率处的信息,传统的状态空间平均法不再适用,因此采用扩展函数描述法(EDF)建立半桥LLC谐振变换器的数学模型。如图1所示为半桥式LLC谐振变换器原理图。

首先,选择激磁电感电流、谐振电感电流以及谐振电容电压作为状态变量,并根据拓扑结构,列写非线性时变状态方程:

(1)
式(1)中:Lr为谐振电感,Lm为激磁电感、Cr1、Cr2为谐振电容。
其次,根据Fourier分解[2]将周期信号分解为正弦函数之和,只考虑基波分量,得到所需的近似大信号模型,系统稳态运行后,变量不随时间变化而变化,因此忽略模型中的时变分量,即可得到稳态工作点求解方程并转化成矩阵形式,最后在稳态工作点附近,进行变量分离,获取系统的小信号数学模型,并表示成矩阵形式。

(2)
其中,
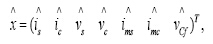


通过以上过程可以得到输出电压对开关频率的关系矩阵:
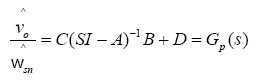
(3)
为进行环路设计,首先需要验证上述方法得到的数学模型的准确性,如表1所示为实际系统参数。

在Saber中搭建仿真模型,逐点仿真。仿真验证结果如图2所示。

为了获得良好的系统动态和稳态特性,需加入补偿环节,因考虑系统的寄生参数[2]后,系统阶数较高,因此在设计补偿环路时,通过加入适当的零极点,来改善系统的频域特性。本文采用PID控制器[3],为实现零极点对消,将PID控制的表达式表示成:
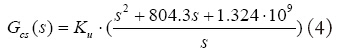
通过调节系数Ku使得系统获较好的低频增益和穿越频率点。如图3所示为补偿前后系统的幅频、相频增益特性曲线。

对比补偿前后系统频域特性,经过补偿的系统特性明显得到了改善,穿越频率[4]在11.8kHz处,相位裕度约为87.5o,符合模拟域的环路设计要求。

1.2 数字控制对环路稳定性的影响
由于数字控制的离散特性,须将所设计的模拟PID控制器在z域下进行稳定性的判定。作为理想的PID控制器,须满足以下条件:一是补偿后控制系统在z域稳定;二是控制器具有可实现性,本节主要通过z变换实现最优PID参数的整定[5]。加入补偿器后时域控制框图如图4所示。
分别对功率级传递函数Gp(s)、补偿器传递函数Gc(s)进行z变换,得到其z域的闭环特征方程:
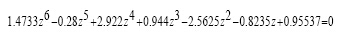
(5)
从而得到补偿后的系统z域闭环零极点分布图,如图5所示。

根据z域稳定性条件[6]:闭环传递函数的极点应位于单位圆内。可以看出,此时在数字离散域中系统是不稳定的,因此必须选用适合于数字控制的PID控制器设计方法。
与传统的模拟控制器相比,数字控制器由于DSP等数字器件的固有特性,需要在设计时进行相关的考虑。数字控制核心DSP采样输出电压获得反馈信号,经过补偿器控制后作为调制信号[7],从而控制输出电压恒定,由此可知,更新驱动脉冲的调制信号与实际采样信号之间存在一个周期的延时,这可以通过加入零阶保持器来模拟。并且由于理想采样开关的存在,使得控制器具有1/Ts的增益特性[8],因此可以得到数字PWM在连续时域设计时的等效模型。
由上面的介绍可知,与数字PWM相关的延时效应可以通过加入ZOH来等效,实际上,采用数字控制器时,还存在另外一种延时效应,即控制算法的计算延时[3],这是由处理器从采样到输出一个新的调制量所需要的计算时间决定的,通常假设该控制延时时间为一个调制周期,即Ts,将此延时加入在模拟控制器设计中,可以通过加入延时环节
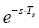
来等效,从而得到以下表达式来模拟数字控制带来的影响。
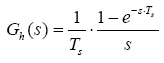
(6)
通过以上分析,本文以z域稳定性作为设计前提,通过降低系统带宽解决控制器计算延时等带来的问题,设计穿越频率为
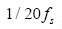
,即开关频率的二十分之一处,保证有足够的相位裕度。考虑数字影响后,系统开环传递函数[9]为:

(7)
将
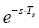
用有理函数之和来等效,得到等效后开环传递函数:

(8)
得到补偿后的开环传递函数:
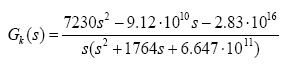
(9)
在Matlab中绘制补偿前后系统开环传递函数的Bode图,如图6所示。

如图6,补偿后系统的开环穿越频率为6.72kHz,相位为88.5°,满足设计要求。同样地,仍需对所设计数字补偿器进行离散域稳定性的验证,对补偿前开环传递函数Gpd(s)以及PID控制器Gcd(s)进行z变换,并乘以
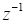
得到z域传递函数。据此绘制其零极点分布图如图7所示。
从图7可以看出,经过重新设计后的PID控制器满足离散控制要求,所设计的系统是稳定的。
2 仿真与实验结果
通过以上分析,得到了相应的PID补偿器,本节以电流闭环为例给出了相应的仿真结果。
2.1 仿真结果
图8所示分别为变换器恒流输出模式下负载突卸、突加的仿真波形。

从仿真波形上可以看出,电流环跟踪性能良好,能够按照指定准确输出,并且动态过程没有过大的冲击,表明本文所设计的环路具有良好的稳态和动态性能。
2.2 实验结果
按照实际系统结构,搭建实验平台,平台包括电源侧、变换器侧以及负载侧,其中电源采用单相调压器进行模拟,调压器额定频率50Hz工频,交流输入220V,输出电压可调范围为0~250V;变换器为由LLC谐波变换器、EMI滤波器、控制芯片等构成的控制平台,其中半桥LLC谐波变换器功率变压器采用EE55磁芯,原副边绕线匝数分别为6、3,变比为2;负载侧由电子负载模拟蓄电池,设备可以作为恒压负载或恒流负载使用,从而模拟蓄电池的恒压充电以及恒流充电特性。
图9为变换器运行于恒流模式,指定输出30A、10A的稳态实验波形以及负载突加、突降时的动态响应实验波形,用以验证本文所设计的数字PID控制器的闭环控制性能。

从图9可以看出,本文所设计的变换器能够按照指定电流进行输出,且稳态性能良好,针对蓄电池负载,变换器可以实时地根据负载情况进行动态跟踪,达到蓄电池充电的目的。
从实验波形上可以看出,实验结果与仿真结果具有较好的一致性,验证了环路的稳态跟踪性能以及动态响应特性。
3 结论
通过扩展函数描述法得到数学模型,给谐振型变换器的建模提供了理论支撑;再通过离散化,在z域验证数字控制式系统的稳定性,证实了数字控制延时等对系统稳定性的影响,最后,根据仿真和实验结果可以看出,本文所设计的系统环路具有良好的稳态跟踪性能和动态响应特性。在此基础上,可以展开进一步研究,寻求除降低系统带宽外更准确的适用于数字控制的环路设计方案,综上所述,本文具有较高的研究和参考价值。
参考文献:
[1]石艳敏. 电动汽车车载智能充电器的研究[D]. 南京:南京理工大学. 2011
[2]Bo Yang.Topology Investigation for Front End DC-DC Power Conversion for Distributed Power System.Virginia Polytechnic Institute and State University.2003
[3]徐建明. PID控制器及其设计方法研究[D].浙江:浙江工业大学. 2002
[4]Simone Buso, Paolo Mattavelli. Digital Control in Power Electronics. 2006
[5]肖献保,冯根生.铅酸蓄电池快速充电技术研究[J].重庆科技学院学报自然科学版,2010,12(4):134-135
[6]周震宇, 张军明, 钱照明. 基于PIC单片机的数字式智能铅酸电池充电器的设计[J]. 电源技术应用,2006,9:18-21
[7]张治国, 谢运祥.LCC谐振变换器的电路特性分析[J].电工技术学报,2013,28(4):50-56
[8]Yanyan Jin,Jianping Xu,Guohua Zhou,etal. Small Signal Modeling of Digital V2 Control for Buck Converter with Pulse Frequency Modulation[J]. IEEE,2010,2(12):102-105
[9]Agasthya Ayachit,Dakshina Murthy-Bellur.Steady-State Analysis of Series Resonant Converter Using Extended Describing Function Method[J]. IEEE,2012,12:1160-1163
[10]Yongsuk Choi, Heungjun Jeon, Yong-Bin Kim. A Switched-Capacitor DC-DC Converter Using Delta-Sigma Digital Pulse Frequency Modulation Control Method[J]. IEEE,2013,66(8):356-359
射频工程师养成培训教程套装,助您快速成为一名优秀射频工程师...
射频和天线工程师培训课程详情>>

