- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
数字升压型功率因数校正转换器的分析与设计
录入:edatop.com 点击:
摘要:本文以升压型转换器为AC-DC功率因数校正整流器的基本结构,控制核心采用DsPIC30F4011数字信号处理器,利用主动式功率因数校正技术的平均电流控制法,提高功率因数,减少输入电流谐波。为避免高功率因数转换器电压回路系统的带宽限制,额外加入负载电流以改善负载变动时输出电压的暂态响应。详细分析转换器、系统建模及控制器设计,开发一个450W的数字升压型功率因数校正转换器,通过试验验证转换器的高功率因数性能及输入电压幅值变动和负载变动时,输出电压的稳压性能。
传统AC/DC整流器因桥式整流器和滤波电容在整流过程中产生脉冲电流,造成低功率因数及电流谐波,需要对功率因数进行校正。理想的AC/DC转换器应具有两种特性:从电网端看须具备高功率因数的特性,从负载端看要有稳压性能。主动功率因数校正电路在运行校正电路连续导通模式(CCM)下,电路不具备功率因数校正的能力,需控制输入电流,使输入电流随输入电压波形及相位变化来提高功率因数[1-3]。利用平均电流控制的功率因数校正转换器对负载变动及输出电压的暂态响应较为迟缓,且需要复杂的控制电路及额外的乘/除器,数字电路等。而Figures[4]提出的负载电流法能有效改善输出电压暂态响应及稳压特性[5-6]。
本文以数字信号处理器DsPIC30F4011为基础,采用平均电流控制法与负载电流注入控制法实现数字控制高功率因数升压型AC/DC转换器系统。整个系统包括内回路电流控制、外回路电压控制及负载电流注入控制,通过该系统能在负载和输入电压幅值变动时,提高转换器的功率因数及输出电压的稳压性能。
1 升压型转换器系统
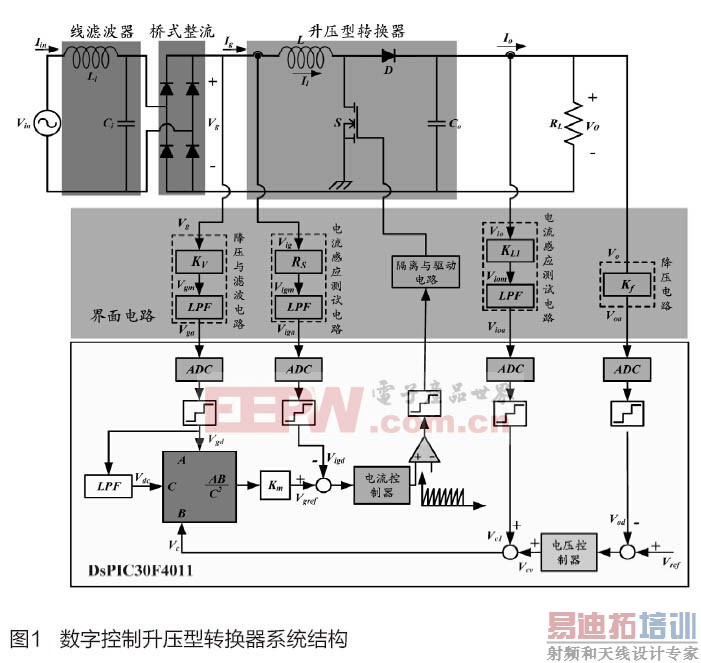
以数字信号处理器为基础的数字控制高功率因数转换器的系统结构如图1所示。其中内回路系统电流控制的作用是使输入电流随输入电压变化,以达到高功率因数性能;外回路电压控制作用是当输入电压幅值及负载变动时,整流器都能具有良好的输出稳压性能;负载电流注入控制的作用是将负载电流状态纳入反馈控制电路,以改善输出电压的暂态响应特性[7-8]。
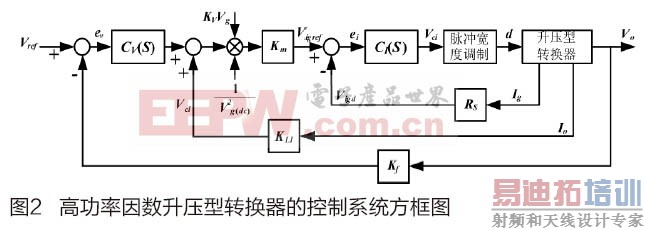
以平均电流控制法为基础的高功率因数升压型转换器的系统方框图如图2所示,为设计内回路电流控制器及外回路电路电压控制器,以提高系统功率因数及输出稳压性能,首先必须对升压型转换器进行分析,并建立受控系统模型,得出相应的数学模型,以此作为控制器设计基础。
2 高功率因数升压型转换器分析与建模
2.1 升压型转换器分析
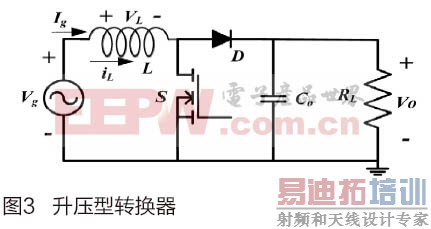
高功率因数升压型转换器如图3所示,经过桥式整流的电压源
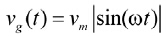
的全波波型,线电压半周期为
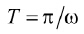
。在稳态分析前,假设:(1)切换周期Ts,开关导通比d;(2)电路运行在连续导通模式;(3)输出电容足够大,使输出电压为固定值V0。
在稳态下,利用伏秒平衡定理有:
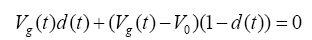
(1)
整理可得:
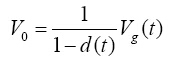
(2)
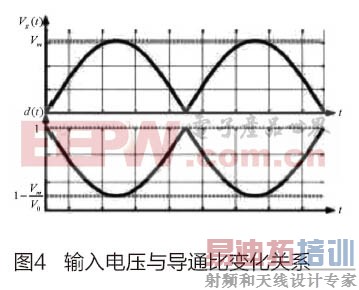
因为od(t)1,输出电压V0恒大于输入电压Vg。稳态时,输入电压与导通比变化关系如图4。
2.2 内回路电流控制系统建模
内回路电流控制的目的是让平均输入电流随输入电压波形变化,以达到高功率因数。通过对比感测电压Vidg与参考电压Viigref,得到误差信号ei,如图2所示。在经过电流控制器CI(S)和脉冲宽度调制器产生导通比d的驱动信号,控制开关的开和关,使平均输入电流随输入电压变化[9-10]。
为设计电流控制器,需建立控制系统的数学模型。本文利用状态空间平均法对升压型转换器作交流小信号分析,推导出控制系统的输出函数,作为CI(S)的设计基础。小信号分析可分为以下步骤:
1. 电路状态方程:升压型转换器如图3,若开关S打开,则二极管关闭,方程为:
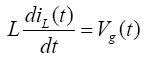
(3)

(4)
若开关S关闭,则二极管打开,方程为:
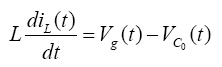
(5)
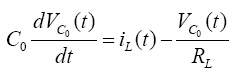
(6)
2. 线性化:对电感电流iL,输入电压Vg,电容电压Vc0,导通比d,忽略直流项及交流乘积项,可得线性方程式:
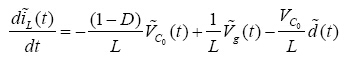
(7)

(8)
3. 传递函数:求出输出信号
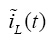
对控制信号导通比
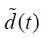
的传递函数为:

(9)
2.3 外回路电压控制系统建模
假设内回路电流控制器CI(S)设计合理,使平均输入电流随输入电压变化,利用平均功率法,对外回路电压控制系统的控制系统建模,求出传递函数,作为电压控制器的设计基础,以达到输出电压的稳压性能。如图2所示的功率因数校正转换器系统方框图,可得:
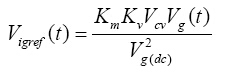
(10)
当
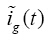
随Vg(t)变化,则
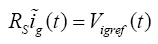
,
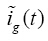
可表示为:
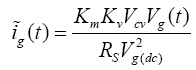
(11)
假设转换器转换效率为100%,即Pin(t)=P0(t),则平均输入功率为:
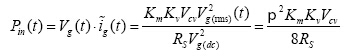
(12)
其中,Vg(t)的均方根值为Vg(nms) 与平均值为Vg(dc) 的比值为
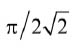
。因此,平均输出功率为:
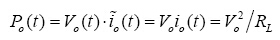
(13)
因此可得:
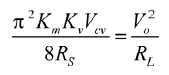
(14)
根据理想高功率因数转换器的无损电阻器模式,如图5所示。对于线电压半周期T2L的移动平均值而言,控制信号发VCV与输入电压平均值Vg(dc) 的变化相当缓慢,可视为常数。
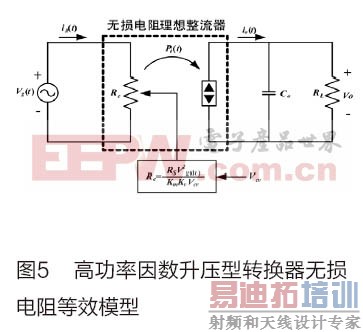
由式(12)和式(14)求得:
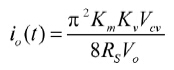
(15)
另一方面,因为

,所以:
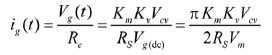
(16)
直流分析:由式(15)和(16)可得直流工作点
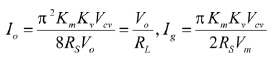
(17)
交流分析:忽略直流项与交流高次项,可得:
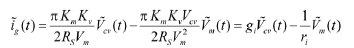
(18)
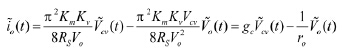
(19)
求得控制信号
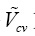
至输出电压
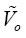
之间的传递函数为:
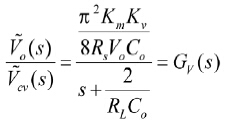
(20)
3 控制器设计与负载电流注入法
设计一个高功率因数升压型AC/DC转换器,其规格为输入电压90~130Vrms、输出电压312V、最大输出功率450W。元件参数为电感L=1Mh,输出电容Co=848uF,负载RL=216,功率开关切换频率fs=100kHz。
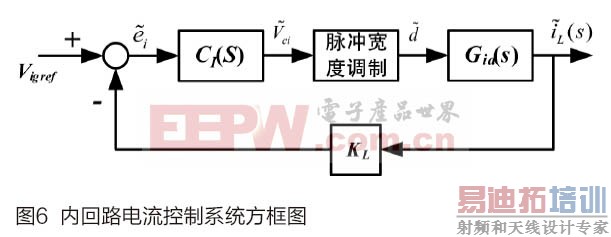
高功率因数升压型转换器的内回路电流控制方框图如图6所示,脉冲宽度调制等效增益为1/10;将电气型号与元件参数值代入式(9)可得:
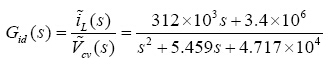
(21)
设计的电流控制器CI(S)为PI控制器GI(s)=0.4+900/s (22)
得到内回路电流控制系统频率与响应,系统的频宽为1.33Hz,满足内回路系统频宽远大于120kHz的要求。
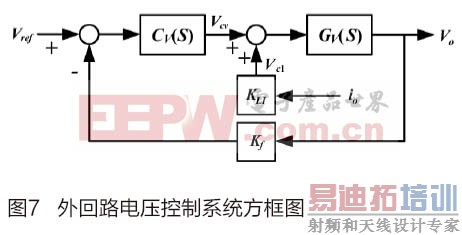
高功率因数转换器的外回路电压控制系统方框图如图7所示,为了使输入电压V0不受输入电压Vm幅值变动及负RL载变动的影响,设计稳压控制器Cv(s),以达到稳压性能。实际中降压比Kv=1/39、Kf=1/104,调整比Km=1000,代入公式(20) 得:
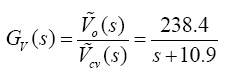
(23)
设计稳压控制器Cv(s)为积分器与相位超前控制器的组合
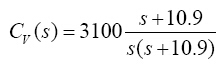
(24)
可得外回路电压控制系统频率响应的波特图如8所示,系统的频宽约为74.9rad/s=11.9Hz,满足步阶响应的稳态误差为零及外回路系统频宽在10Hz~20Hz的要求。
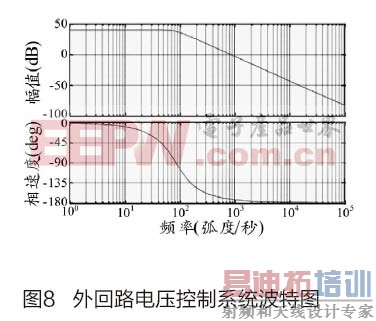
为实现数字控制,将控制器传递函数转换成离散时间状态的空间表示式,在取样频率为6kHz下,得到电流控制器为:
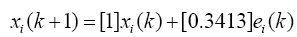
(25)
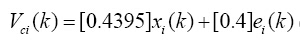
(26)
同样地,在取样频率为2kHz下,可得电压控制器离散状态空间表示为:
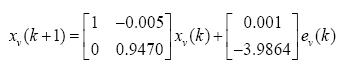
(27)
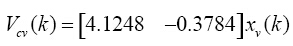
(28)
在外回路电压控制器设计上,为减少控制器信号与乘法器信号受120Hz输出电压的影响,降低了功率因数的性能,所以外回路系统的频宽通常设计在10Hz~20Hz之间。因此,在负载变动时,输出电压很难恢复至稳压状态。本文利用负载电流注入法将负载电流状态作为控制反馈,以改善输出电压的暂态响应。负载电流注入法是将负载电流接入控制回路,当负载发生变动时,立刻产生稳态输入电流的参考信号,改善外回路电压控制器缓慢的动态响应。
4 数字控制系统试验验证
以16位数字信号处理器DsPIC30F4011为基础,完成数字控制高功率因数升压型转换器的设计。在试验验证过程中,输入电压90~130 Vrms、输出电压312 V、最大输出功率450 W的高功率因数升压型AC/DC转换器。试验测量结果如下:
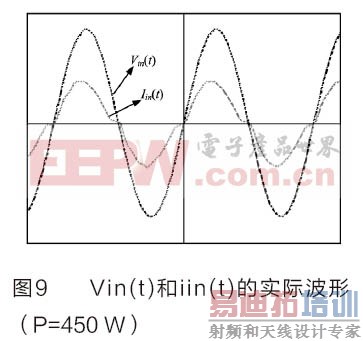
图9为输入电压110Vrms、输出功率450W时,输入电压Vin和电流iin的实际波型,利用万用表测量的功率因数值为0.968,说明了该设计系统的高功率因数特性。
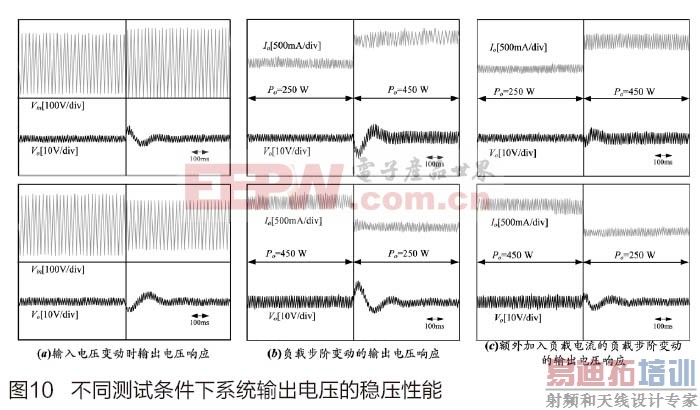
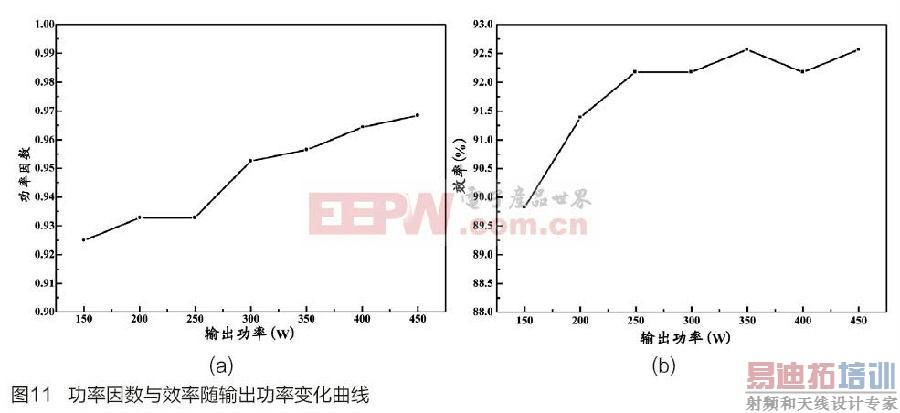
随后,对系统输出电压的稳压性能进行测试,针对输入电压从110 V变动到130 V,再从110 V变到90 V,输出的电压响应如图10(a)。当负载从250 W变动到450 W时,输出的电压响应如图10(b)。当额外加入负载电流且负载变动同时发生时,输出的电压响应如图10(c)。比较图10(b)和10(c),图10(c)的输出电压变动较小时,负载电流注入法具有较高的稳压效果。当Vin=110 Vrms时,针对不同输出功率,测得高功率因数升压型转换器的功率因数曲线如图11(a)所示,在Po=450W时,功率因数最高可达0.966。针对不同输出功率,测量高功率因数升压型转换器的效率曲线如图11(b)所示,在Po=450W时,效率最高可达92.2%。
5 结论
本文以升压型转换器为AC/DC功率因数校正整流器的基本结构,以数字信号处理器DsPIC30F4011为控制核心,应用主动式功率因数校正技术的平均电流控制法,使平均输入电流随输入电压波形变化,以提高功率因数性能。利用负载电流注入控制法,改善输出电压动态响应较慢的缺点。最后设计输出功率为450W的高功率因数升压型转换器并进行试验,试验结果表明,该功率因数升压型转换器符合电流谐波的高功率因数特性,并且在输入电压幅值变动及负载变动时,输出具有良好的稳压特性。
参考文献:
[1]周志敏, 周纪海. 开关电源功率因数校正电路设计与应用[M]. 北京: 人民邮电出版社出版, 2004
[2]宗凡. Boost APFC电路的设计与实现[D]. 西安: 西北工业大学, 2006
[3]王志强等译. Abraham I. Pressman著. 开关电源设计[M]. 北京: 电子工业出版社, 2005
[4]E. Figures, J.M Benavent, G. Garcer’a, M. Pascual. A control circuit with load-current injection for single-phase power-factor-correction rectifiers[J]. IEEE Trans. Industrial Electronics, 2007, (54):1272-1281
[5]A.J Prodic, R.W. Chen, Erikson, D. Maksimovic. Digitally controlled low-harmonic rectifier having fast dynamic response[C]. IEEE APEC, 2002, 476-482
[6]S. Buso, P. Mattavelli, L. Rossetto, G. Spiazzi. Simple digital control improving dynamic performance of power factor preregulators[J]. IEEE Trans. Power Electronics, 1998, 13(5): 814-823
[7]M.G. Villalva, J.R. Gazoli, E.R. Filho. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays [J]. IEEE Transactions on Power Electronics, 2009, 24(5): 1198-2008
[8]L. Fangrui, D. Shanxu, L. Fei, L. Bangyin, K. Yong. A Variable Step Size INC MPPT Method for PV Systems [J]. IEEE Transactions on Industrial Electronics, 2008, (55): 2622-28
[9]R.W. Erickson, D. Maksimovic. Fundamentals of power electronics[M]. Kluwer Academic Publishers, 2001, Second Edition
[10]J.L. Lin, C.Y. Chen, Y.K. Wang. AC/DC converter analysis based on LFR model[C]. Proceeding of Taiwan Power Electronics Conference. 2006, 1015-1020
传统AC/DC整流器因桥式整流器和滤波电容在整流过程中产生脉冲电流,造成低功率因数及电流谐波,需要对功率因数进行校正。理想的AC/DC转换器应具有两种特性:从电网端看须具备高功率因数的特性,从负载端看要有稳压性能。主动功率因数校正电路在运行校正电路连续导通模式(CCM)下,电路不具备功率因数校正的能力,需控制输入电流,使输入电流随输入电压波形及相位变化来提高功率因数[1-3]。利用平均电流控制的功率因数校正转换器对负载变动及输出电压的暂态响应较为迟缓,且需要复杂的控制电路及额外的乘/除器,数字电路等。而Figures[4]提出的负载电流法能有效改善输出电压暂态响应及稳压特性[5-6]。
本文以数字信号处理器DsPIC30F4011为基础,采用平均电流控制法与负载电流注入控制法实现数字控制高功率因数升压型AC/DC转换器系统。整个系统包括内回路电流控制、外回路电压控制及负载电流注入控制,通过该系统能在负载和输入电压幅值变动时,提高转换器的功率因数及输出电压的稳压性能。
1 升压型转换器系统
以数字信号处理器为基础的数字控制高功率因数转换器的系统结构如图1所示。其中内回路系统电流控制的作用是使输入电流随输入电压变化,以达到高功率因数性能;外回路电压控制作用是当输入电压幅值及负载变动时,整流器都能具有良好的输出稳压性能;负载电流注入控制的作用是将负载电流状态纳入反馈控制电路,以改善输出电压的暂态响应特性[7-8]。

以平均电流控制法为基础的高功率因数升压型转换器的系统方框图如图2所示,为设计内回路电流控制器及外回路电路电压控制器,以提高系统功率因数及输出稳压性能,首先必须对升压型转换器进行分析,并建立受控系统模型,得出相应的数学模型,以此作为控制器设计基础。

2 高功率因数升压型转换器分析与建模
2.1 升压型转换器分析
高功率因数升压型转换器如图3所示,经过桥式整流的电压源
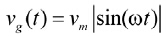
的全波波型,线电压半周期为
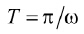
。在稳态分析前,假设:(1)切换周期Ts,开关导通比d;(2)电路运行在连续导通模式;(3)输出电容足够大,使输出电压为固定值V0。

在稳态下,利用伏秒平衡定理有:
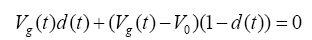
(1)
整理可得:
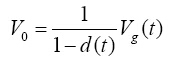
(2)
因为od(t)1,输出电压V0恒大于输入电压Vg。稳态时,输入电压与导通比变化关系如图4。

2.2 内回路电流控制系统建模
内回路电流控制的目的是让平均输入电流随输入电压波形变化,以达到高功率因数。通过对比感测电压Vidg与参考电压Viigref,得到误差信号ei,如图2所示。在经过电流控制器CI(S)和脉冲宽度调制器产生导通比d的驱动信号,控制开关的开和关,使平均输入电流随输入电压变化[9-10]。
为设计电流控制器,需建立控制系统的数学模型。本文利用状态空间平均法对升压型转换器作交流小信号分析,推导出控制系统的输出函数,作为CI(S)的设计基础。小信号分析可分为以下步骤:
1. 电路状态方程:升压型转换器如图3,若开关S打开,则二极管关闭,方程为:
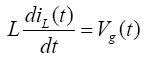
(3)

(4)
若开关S关闭,则二极管打开,方程为:
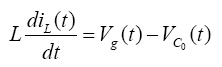
(5)
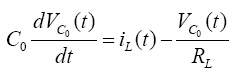
(6)
2. 线性化:对电感电流iL,输入电压Vg,电容电压Vc0,导通比d,忽略直流项及交流乘积项,可得线性方程式:
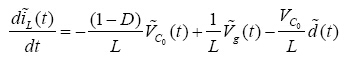
(7)

(8)
3. 传递函数:求出输出信号
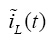
对控制信号导通比
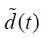
的传递函数为:

(9)
2.3 外回路电压控制系统建模
假设内回路电流控制器CI(S)设计合理,使平均输入电流随输入电压变化,利用平均功率法,对外回路电压控制系统的控制系统建模,求出传递函数,作为电压控制器的设计基础,以达到输出电压的稳压性能。如图2所示的功率因数校正转换器系统方框图,可得:
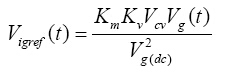
(10)
当
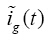
随Vg(t)变化,则
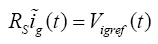
,
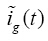
可表示为:
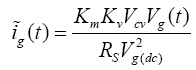
(11)
假设转换器转换效率为100%,即Pin(t)=P0(t),则平均输入功率为:
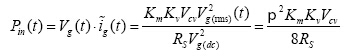
(12)
其中,Vg(t)的均方根值为Vg(nms) 与平均值为Vg(dc) 的比值为
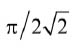
。因此,平均输出功率为:
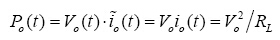
(13)
因此可得:
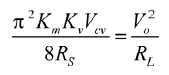
(14)
根据理想高功率因数转换器的无损电阻器模式,如图5所示。对于线电压半周期T2L的移动平均值而言,控制信号发VCV与输入电压平均值Vg(dc) 的变化相当缓慢,可视为常数。

由式(12)和式(14)求得:
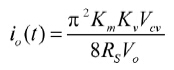
(15)
另一方面,因为

,所以:
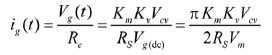
(16)
直流分析:由式(15)和(16)可得直流工作点
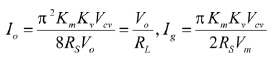
(17)
交流分析:忽略直流项与交流高次项,可得:
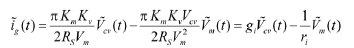
(18)
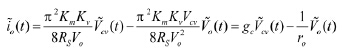
(19)
求得控制信号
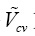
至输出电压
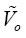
之间的传递函数为:
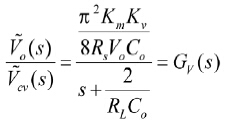
(20)
3 控制器设计与负载电流注入法
设计一个高功率因数升压型AC/DC转换器,其规格为输入电压90~130Vrms、输出电压312V、最大输出功率450W。元件参数为电感L=1Mh,输出电容Co=848uF,负载RL=216,功率开关切换频率fs=100kHz。

高功率因数升压型转换器的内回路电流控制方框图如图6所示,脉冲宽度调制等效增益为1/10;将电气型号与元件参数值代入式(9)可得:
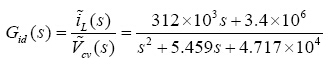
(21)
设计的电流控制器CI(S)为PI控制器GI(s)=0.4+900/s (22)
得到内回路电流控制系统频率与响应,系统的频宽为1.33Hz,满足内回路系统频宽远大于120kHz的要求。

高功率因数转换器的外回路电压控制系统方框图如图7所示,为了使输入电压V0不受输入电压Vm幅值变动及负RL载变动的影响,设计稳压控制器Cv(s),以达到稳压性能。实际中降压比Kv=1/39、Kf=1/104,调整比Km=1000,代入公式(20) 得:
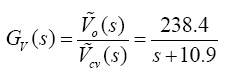
(23)
设计稳压控制器Cv(s)为积分器与相位超前控制器的组合
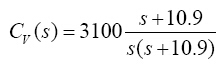
(24)
可得外回路电压控制系统频率响应的波特图如8所示,系统的频宽约为74.9rad/s=11.9Hz,满足步阶响应的稳态误差为零及外回路系统频宽在10Hz~20Hz的要求。

为实现数字控制,将控制器传递函数转换成离散时间状态的空间表示式,在取样频率为6kHz下,得到电流控制器为:
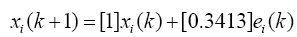
(25)
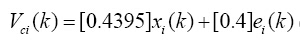
(26)
同样地,在取样频率为2kHz下,可得电压控制器离散状态空间表示为:
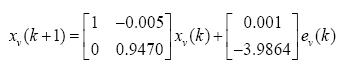
(27)
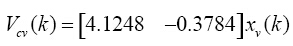
(28)
在外回路电压控制器设计上,为减少控制器信号与乘法器信号受120Hz输出电压的影响,降低了功率因数的性能,所以外回路系统的频宽通常设计在10Hz~20Hz之间。因此,在负载变动时,输出电压很难恢复至稳压状态。本文利用负载电流注入法将负载电流状态作为控制反馈,以改善输出电压的暂态响应。负载电流注入法是将负载电流接入控制回路,当负载发生变动时,立刻产生稳态输入电流的参考信号,改善外回路电压控制器缓慢的动态响应。
4 数字控制系统试验验证
以16位数字信号处理器DsPIC30F4011为基础,完成数字控制高功率因数升压型转换器的设计。在试验验证过程中,输入电压90~130 Vrms、输出电压312 V、最大输出功率450 W的高功率因数升压型AC/DC转换器。试验测量结果如下:

图9为输入电压110Vrms、输出功率450W时,输入电压Vin和电流iin的实际波型,利用万用表测量的功率因数值为0.968,说明了该设计系统的高功率因数特性。

随后,对系统输出电压的稳压性能进行测试,针对输入电压从110 V变动到130 V,再从110 V变到90 V,输出的电压响应如图10(a)。当负载从250 W变动到450 W时,输出的电压响应如图10(b)。当额外加入负载电流且负载变动同时发生时,输出的电压响应如图10(c)。比较图10(b)和10(c),图10(c)的输出电压变动较小时,负载电流注入法具有较高的稳压效果。当Vin=110 Vrms时,针对不同输出功率,测得高功率因数升压型转换器的功率因数曲线如图11(a)所示,在Po=450W时,功率因数最高可达0.966。针对不同输出功率,测量高功率因数升压型转换器的效率曲线如图11(b)所示,在Po=450W时,效率最高可达92.2%。

5 结论
本文以升压型转换器为AC/DC功率因数校正整流器的基本结构,以数字信号处理器DsPIC30F4011为控制核心,应用主动式功率因数校正技术的平均电流控制法,使平均输入电流随输入电压波形变化,以提高功率因数性能。利用负载电流注入控制法,改善输出电压动态响应较慢的缺点。最后设计输出功率为450W的高功率因数升压型转换器并进行试验,试验结果表明,该功率因数升压型转换器符合电流谐波的高功率因数特性,并且在输入电压幅值变动及负载变动时,输出具有良好的稳压特性。
参考文献:
[1]周志敏, 周纪海. 开关电源功率因数校正电路设计与应用[M]. 北京: 人民邮电出版社出版, 2004
[2]宗凡. Boost APFC电路的设计与实现[D]. 西安: 西北工业大学, 2006
[3]王志强等译. Abraham I. Pressman著. 开关电源设计[M]. 北京: 电子工业出版社, 2005
[4]E. Figures, J.M Benavent, G. Garcer’a, M. Pascual. A control circuit with load-current injection for single-phase power-factor-correction rectifiers[J]. IEEE Trans. Industrial Electronics, 2007, (54):1272-1281
[5]A.J Prodic, R.W. Chen, Erikson, D. Maksimovic. Digitally controlled low-harmonic rectifier having fast dynamic response[C]. IEEE APEC, 2002, 476-482
[6]S. Buso, P. Mattavelli, L. Rossetto, G. Spiazzi. Simple digital control improving dynamic performance of power factor preregulators[J]. IEEE Trans. Power Electronics, 1998, 13(5): 814-823
[7]M.G. Villalva, J.R. Gazoli, E.R. Filho. Comprehensive Approach to Modeling and Simulation of Photovoltaic Arrays [J]. IEEE Transactions on Power Electronics, 2009, 24(5): 1198-2008
[8]L. Fangrui, D. Shanxu, L. Fei, L. Bangyin, K. Yong. A Variable Step Size INC MPPT Method for PV Systems [J]. IEEE Transactions on Industrial Electronics, 2008, (55): 2622-28
[9]R.W. Erickson, D. Maksimovic. Fundamentals of power electronics[M]. Kluwer Academic Publishers, 2001, Second Edition
[10]J.L. Lin, C.Y. Chen, Y.K. Wang. AC/DC converter analysis based on LFR model[C]. Proceeding of Taiwan Power Electronics Conference. 2006, 1015-1020
射频工程师养成培训教程套装,助您快速成为一名优秀射频工程师...
射频和天线工程师培训课程详情>>

