- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
开关电源的建模和环路补偿设计(1):小信号建模的基本概念和方法
录入:edatop.com 点击:
引言
如今的电子系统变得越来越复杂,电源轨和电源数量都在不断增加。为了实现最佳电源解决方案密度、可靠性和成本,系统设计师常常需要自己设计电源解决方案,而不是仅仅使用商用砖式电源。设计和优化高性能开关模式电源正在成为越来越频繁、越来越具挑战性的任务。
电源环路补偿设计常常被看作是一项艰难的任务,对经验不足的电源设计师尤其如此。在实际补偿设计中,为了调整补偿组件的值,常常需要进行无数次迭代。对于一个复杂系统而言,这不仅耗费大量时间,而且也不够准确,因为这类系统的电源带宽和稳定性裕度可能受到几种因素的影响。本应用指南针对开关模式电源及其环路补偿设计,说明了小信号建模的基本概念和方法。本文以降压型转换器作为典型例子,但是这些概念也能适用于其他拓扑。本文还介绍了用户易用的 LTpowerCAD设计工具,以减轻设计及优化负担。
确定问题
一个良好设计的开关模式电源 (SMPS) 必须是没有噪声的,无论从电气还是声学角度来看。欠补偿系统可能导致运行不稳定。不稳定电源的典型症状包括:磁性组件或陶瓷电容器产生可听噪声、开关波形中有抖动、输出电压震荡、功率 FET 过热等等。
不过,除了环路稳定性,还有很多原因可能导致产生不想要的震荡。不幸的是,对于经验不足的电源设计师而言,这些震荡在示波器上看起来完全相同。即使对于经验丰富的工程师,有时确定引起不稳定性的原因也是很困难。图 1 显示了一个不稳定降压型电源的典型输出和开关节点波形。调节环路补偿可能或不可能解决电源不稳定问题,因为有时震荡是由其他因素引起的,例如 PCB 噪声。如果设计师对各种可能性没有了然于胸,那么确定引起运行噪声的潜藏原因可能耗费大量时间,令人非常沮丧。
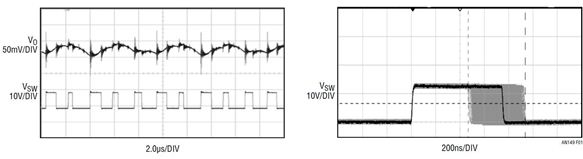
图 1:一个 “不稳定” 降压型转换器的典型输出电压和开关节点波形
对于开关模式电源转换器而言,例如图 2 所示的 LTC3851 或LTC3833 电流模式降压型电源,一种快速确定运行不稳定是否由环路补偿引起的方法是,在反馈误差放大器输出引脚 (ITH) 和 IC 地之间放置一个 0.1μF 的大型电容器。(或者,就电压模式电源而言,这个电容器可以放置在放大器输出引脚和反馈引脚之间。) 这个 0.1μF 的电容器通常被认为足够大,可以将环路带宽拓展至低频,因此可确保电压环路稳定性。如果用上这个电容器以后,电源变得稳定了,那么问题就有可能用环路补偿解决。
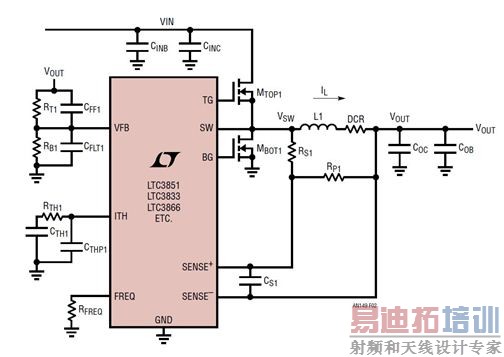
图 2:典型降压型转换器 (LTC3851、LTC3833、LTC3866 等)
过补偿系统通常是稳定的,但是带宽很小,瞬态响应很慢。这样的设计需要过大的输出电容以满足瞬态调节要求,这增大了电源的总体成本和尺寸。图 3 显示了降压型转换器在负载升高 / 降低瞬态时的典型输出电压和电感器电流波形。图 3a 是稳定但带宽 (BW) 很小的过补偿系统的波形,从波形上能看到,在瞬态时有很大的 VOUT 下冲 / 过冲。图 3b 是大带宽、欠补偿系统的波形,其中 VOUT 的下冲 / 过充小得多,但是波形在稳态时不稳定。图 3c 显示了一个设计良好的电源之负载瞬态波形,该电源具备快速和稳定的环路。
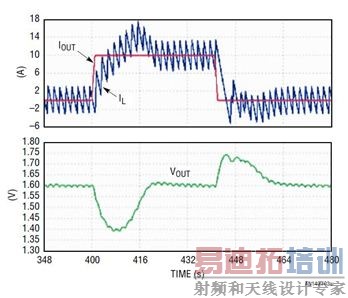
(a) 带宽较小但稳定
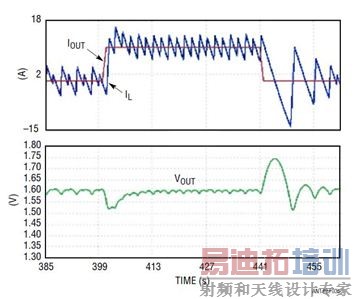
(b) 带宽较大但不稳定
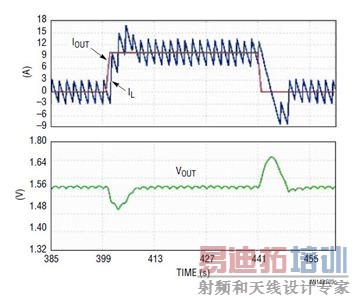
(c) 具快速和稳定环路的最佳设计
图 3:典型负载瞬态响应 ━ (a) 过补偿系统;(b) 欠补偿系统;(c) 具快速和稳定环路的最佳设计
PWM 转换器功率级的小信号建模
开关模式电源 (SMPS),例如图 4 中的降压型转换器,通常有两种工作模式,采取哪种工作模式取决于其主控开关的接通 / 断开状态。因此,该电源是一个随时间变化的非线性系统。为了用常规线性控制方法分析和设计补偿电路,人们在 SMPS 电路稳态工作点附近,应用针对 SMPS 电路的线性化方法,开发了一种平均式、小信号线性模型。
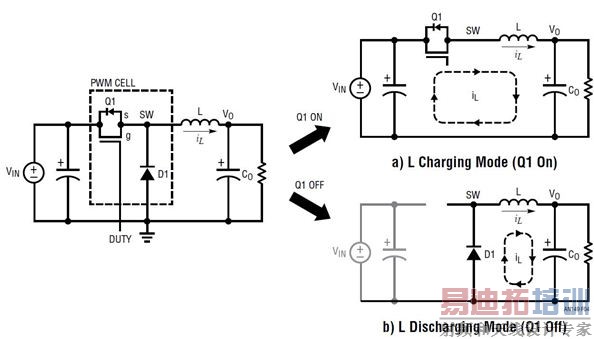
图 4:降压型 DC/DC 转换器及其在一个开关周期 TS 内的两种工作模式
建模步骤 1:通过在 TS 平均,变成不随时间变化的系统
所有 SMPS 电源拓扑 (包括降压型、升压型或降压/升压型转换器) 都有一个典型的 3 端子 PWM 开关单元,该单元包括有源控制开关 Q 和无源开关 (二极管) D。为了提高效率,二极管 D 可以用同步 FET 代替,代替以后,仍然是一个无源开关。有源端子 “a” 是有源开关端子。无源端子 “p” 是无源开关端子。在转换器中,端子 a 和端子 p 始终连接到电压源,例如降压型转换器中的 VIN 和地。公共端子 “c” 连接至电流源,在降压型转换器中就是电感器。
为了将随时间变化的 SMPS 变成不随时间变化的系统,可以通过将有源开关 Q 变成平均式电流源、以及将无源开关 (二极管) D 变成平均式电压源这种方式,应用 3 端子 PWM 单元平均式建模方法。平均式开关 Q 的电流等于 d ● iL,而平均式开关 D 的电压等于 d ● vap,,如图 5 所示。平均是在一个开关周期 TS 之内进行的。既然电流源和电压源都是两个变量的乘积,那么该系统仍然是非线性系统。
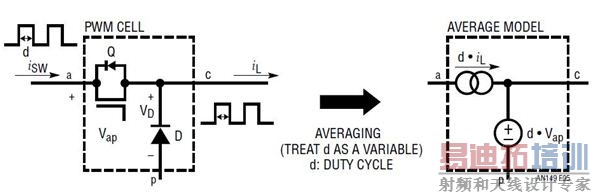
图 5:建模步骤 1:将 3 端子 PWM 开关单元变成平均式电流源和电压源
建模步骤 2:线性AC 小信号建模
下一步是展开变量的乘积以得到线性 AC 小信号模型。例如,变量
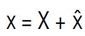
,其中 X 是 DC 稳态的工作点,而
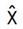
是 AC 小信号围绕 X 的变化。因此,两个变量 x ● y 的积可以重写为:
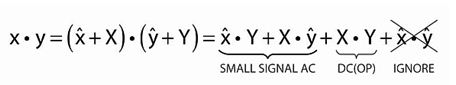
图 6:为线性小信号 AC 部分和 DC 工作点展开两个变量的乘积
图 6 显示,线性小信号 AC 部分可以与 DC 工作点 (OP) 部分分开。两个 AC 小信号变量 (
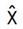
●
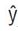
) 的乘积可以忽略,因为这是更加小的变量。按照这一概念,平均式 PWM 开关单元可以重画为如图 7 所示的电路。
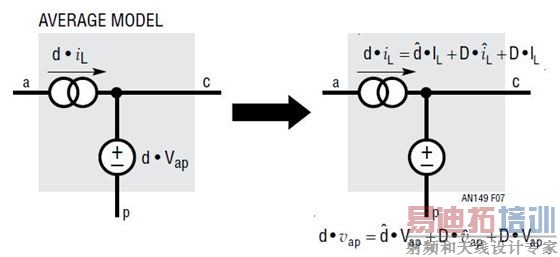
图 7:建模步骤 2:通过展开两个变量的乘积给 AC 小信号建模
通过将上述两步建模方法应用到降压型转换器上 (如图 8 所示),该降压型转换器的功率级就可以建模为简单的电压源

,其后跟随的是一个 L/C 二阶滤波器网络。
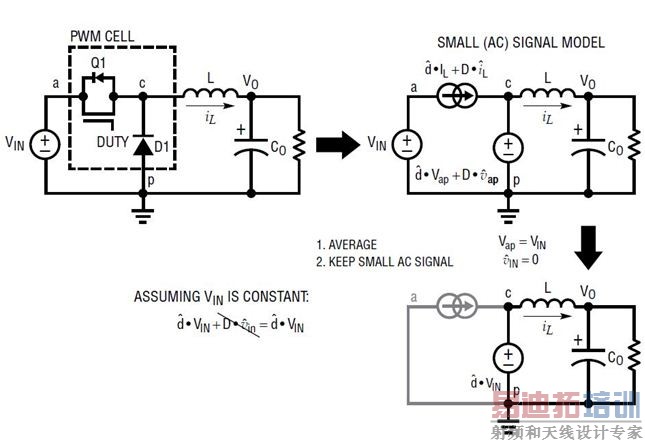
图 8:将降压型转换器变成平均式、AC 小信号线性电路
以图 8 所示线性电路为基础,既然控制信号是占空比 d,输出信号是 vOUT,那么在频率域,该降压型转换器就可以用占空比至输出的转移函数 Gdv(s) 来描述:
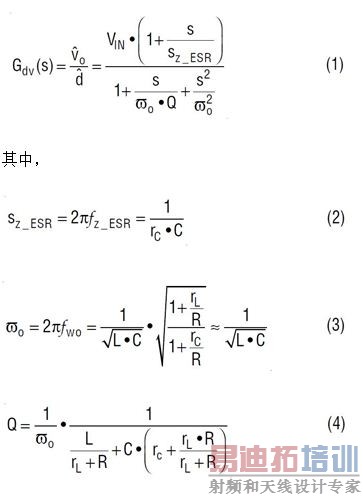
函数 Gdv(s) 显示,该降压型转换器的功率级是一个二阶系统,在频率域有两个极点和一个零点。零点 sZ_ESR 由输出电容器 C 及其 ESR rC 产生。谐振双极点
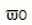
由输出滤波器电感器 L 和电容器 C 产生。
既然极点和零点频率是输出电容器及其 ESR 的函数,那么函数 Gdv(s) 的波德图随所选择电源输出电容器的不同而变化,如图 9 所示。输出电容器的选择对该降压型转换器功率级的小信号特性影响很大。如果该电源使用小型输出电容或 ESR 非常低的输出电容器,那么 ESR 零点频率就可能远远高于谐振极点频率。功率级相位延迟可能接近 –180°。结果,当负压反馈环路闭合时,可能很难补偿该环路。
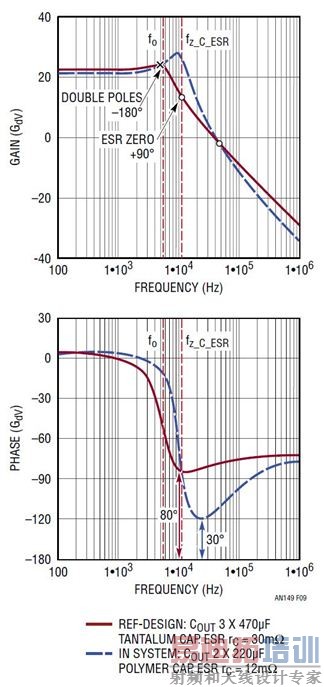
图 9:COUT 电容器变化导致功率级 Gdv(s) 相位显著变化
升压型转换器的小信号模型
利用同样的 3 端子 PWM 开关单元平均式小信号建模方法,也可以为升压型转换器建模。图 10 显示了怎样为升压型转换器建模,并将其转换为线性 AC 小信号模型电路。
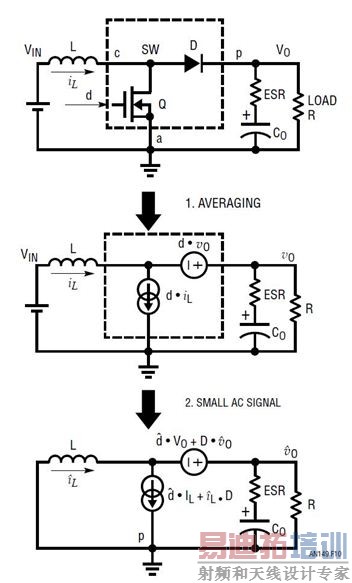
图 10:升压型转换器的 AC 小信号建模电路
升压型转换器功率级的转移函数 Gdv(s) 可从等式 5 中得出。它也是一个二阶系统,具有 L/C 谐振。与降压型转换器不同,升压型转换器除了 COUT ESR 零点,还有一个右半平面零点 (RHPZ) 。该 RHPZ 导致增益升高,但是相位减小 (变负)。等式 6 也显示,这个 RHPZ 随占空比和负载电阻不同而变化。既然占空比是 VIN 的函数,那么升压型转换器功率级的转移函数 Gdv(s) 就随 VIN和负载电流而变。在低 VIN 和大负载 IOUT_MAX时,RHPZ 位于最低频率处,并导致显著的相位滞后。这就使得难以设计带宽很大的升压型转换器。作为一个一般的设计原则,为了确保环路稳定性,人们设计升压型转换器时,限定其带宽低于其最低 RHPZ 频率的 1/10。其他几种拓扑,例如正至负降压 / 升压、反激式 (隔离型降压 / 升压)、SEPIC 和 CUK 转换器,所有都存在不想要的 RHPZ,都不能设计成带宽很大、瞬态响应很快的解决方案。

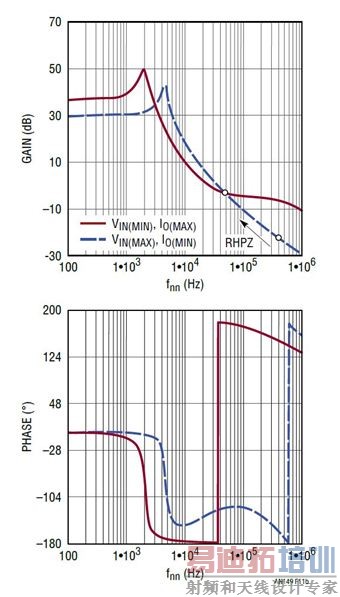
图 11:升压型转换器功率级小信号占空比至 VO 转移函数随 VIN 和负载而改变
用电压模式控制闭合反馈环路
输出电压可以由闭合的反馈环路系统调节。例如,在图 12 中,当输出电压 VOUT 上升时,反馈电压 VFB 上升,负反馈误差放大器的输出下降,因此占空比 d 下降。结果,VOUT 被拉低,以使 VFB = VREF。误差运算放大器的补偿网络可以是 I 型、II 型或 III 型反馈放大器网络。只有一个控制环路调节 VOUT。这种控制方法称为电压模式控制。凌力尔特公司的 LTC3861 和 LTC3882就是典型的电压模式降压型控制器。
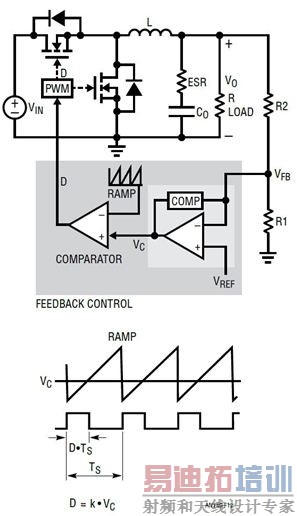
图 12:具闭合电压反馈环路的电压模式降压型转换器方框图
为了优化电压模式 PWM 转换器,如图 13 所示,通常需要一种复杂的 III 型补偿网络,以凭借充足的相位裕度设计一个快速环路。如等式 7 和图 14 所示,这种补偿网络在频率域有 3 个极点和两个零点:低频积分极点 (1/s) 提供高的 DC 增益,以最大限度减小 DC 调节误差,两个零点放置在系统谐振频率 f0 附近,以补偿由功率级的 L 和 C 引起的 –180° 相位延迟,在 fESR 处放置第一个高频极点,以消除 COUT ESR 零点,第二个高频极点放置在想要的带宽 fC 以外,以衰减反馈环路中的开关噪声。III 型补偿相当复杂,因为这种补偿需要 6 个 R/C 值。找到这些值的最佳组合是个非常耗时的任务。
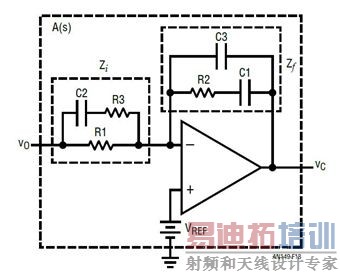
图 13:用于电压模式转换器的 III 型反馈补偿网络

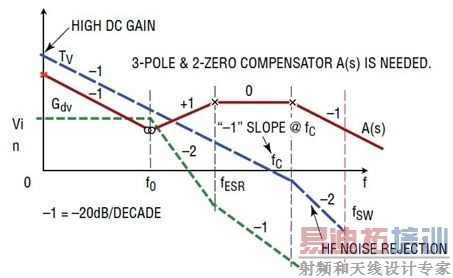
图 14:III 型补偿 A(s) 提供 3 个极点和两个零点,以实现最佳的总体环路增益 TV(s)
为了简化和自动化开关模式电源设计,凌力尔特开发了 LTpowerCAD 设计工具。这工具使环路补偿设计任务变得简单多了。LTpowerCAD 是一款可在 www.linear.com.cn/LTpowerCAD 免费下载的设计工具。该软件帮助用户选择电源解决方案、设计功率级组件以及优化电源效率和环路补偿。如图 15 例子所示,就给定的凌力尔特电压模式控制器而言 (例如 LTC3861),其环路参数可用该设计工具建模。对于一个给定的功率级,用户可以确定极点和零点位置 (频率),然后按照该软件的指导,带入真实的 R/C 值,实时检查总体环路增益和负载瞬态性能。之后,设计方案还可以输出到一个 LTspice 仿真电路上,进行实时仿真。
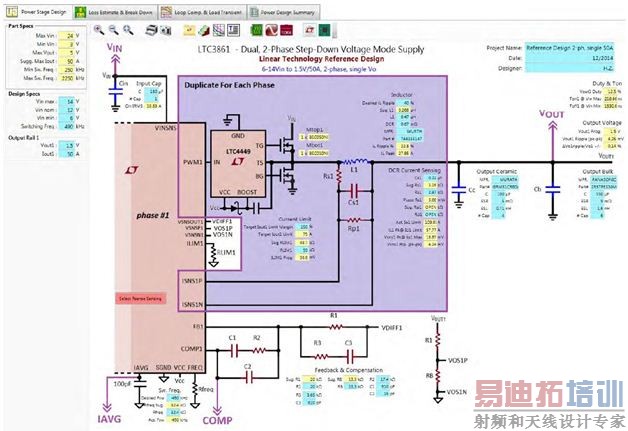
(a) LTpowerCAD 功率级设计页面
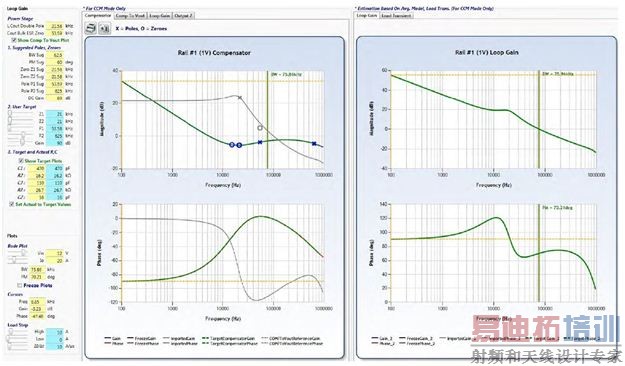
(b) LTpowerCAD 环路补偿和负载瞬态设计页面
图 15:LTpowerCAD 设计工具减轻了电压模式转换器 III 型环路设计的负担
(从 www.linear.com.cn/LTpowerCAD 免费下载)
为电流模式控制增加电流环路
单一环路电压模式控制受到一些限制。这种模式需要相当复杂的 III 型补偿网络。环路性能可能随输出电容器参数及寄生性变化而出现大幅改化,尤其是电容器 ESR 和 PCB 走线阻抗。一个可靠的电源还需要快速过流保护,这就需要一种快速电流检测方法和快速保护比较器。对于需要很多相位并联的大电流解决方案而言,还需要一个额外的电流均分网络 / 环路。
给电压模式转换器增加一个内部电流检测通路和反馈环路,使其变成一个电流模式控制的转换器。图 16 和 17 显示了典型峰值电流模式降压型转换器及其工作方式。内部时钟接通顶端的控制 FET。之后,只要所检测的峰值电感器电流信号达到放大器 ITH 引脚电压 V C,顶端的 FET 就断开。从概念上来看,电流环路使电感器成为一个受控电流源。因此,具闭合电流环路的功率级变成了 1 阶系统,而不是具 L/C 谐振的 2 阶系统。结果,功率级极点引起的相位滞后从 180° 减少为约 90°。相位延迟减少使补偿外部电压环路变得容易多了。相位延迟减少还降低了电源对输出电容器或电感变化的敏感度,如图 18 所示。
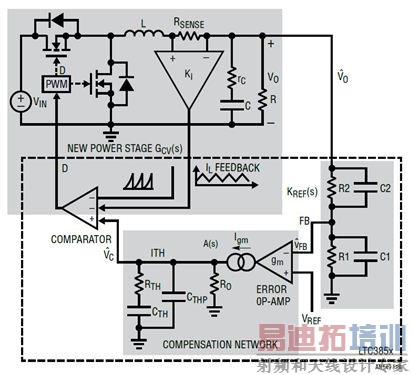
图 16:具内部电流环路和外部电压反馈环路的电流模式转换器方框图
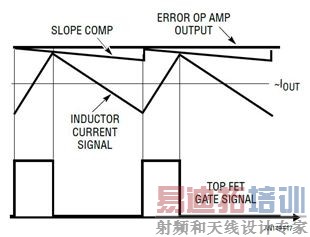
图 17:峰值电流模式控制信号波形
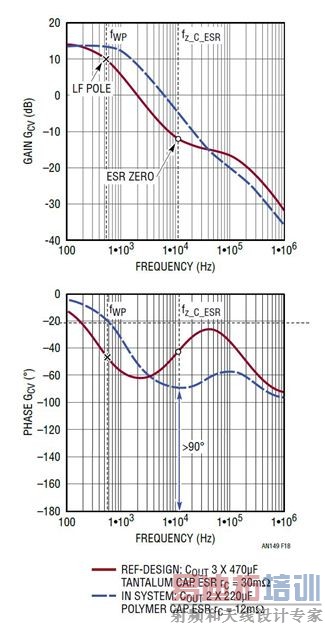
图 18:具闭合电流环路的新功率级转移函数 GCV(s)
电感器电流信号可以直接用一个附加的 RSENSE检测,或者间接地通过电感器绕组 DCR 或 FET RDS(ON)检测。电流模式控制还提供其他几项重要的好处。如图 17 所示,既然电感器电流以逐周期方式、通过放大器输出电压检测和限制,那么系统在过载或电感器电流饱和时,就能够更准确和更快速地限制电流。在加电或输入电压瞬态时,电感器浪涌电流也受到了严格控制。当多个转换器 / 相位并联时,通过将放大器 ITH 引脚连到一起,凭借电流模式控制,可以在多个电源之间非常容易地均分电流,从而实现了一个可靠的多项 (PolyPhase) 设计。典型电流模式控制器包括凌力尔特公司的 LTC3851A、LTC3833 和 LTC3855 等。
峰值与谷值电流模式控制方法
图 16 和 17 所示的电流模式控制方法是峰值电感器电流模式控制。转换器以固定开关频率 fSW工作,从而非常容易实现时钟同步和相位交错,尤其是对于并联转换器。然而,如果在控制 FET 栅极关断后,紧接着就发生负载升压瞬态,那么转换器就必须等待一段时间,这段时间等于 FET 断开时间 TOFF,直到下一个时钟周期响应该瞬态为止。这个 TOFF 延迟通常不是问题,但是对于一个真正的快速瞬态系统,它却很重要。此外,控制 FET 的最短接通时间 (TON_min) 不可能非常短,因为电流比较器需要噪声消隐时间以避免错误触发。对于高 VIN/VOUT 降压比应用而言,这限制了最高开关频率 fSW。此外,峰值电流模式控制还需要一定的斜率补偿,以在占空比超过 50% 时保持电流环路稳定。对于凌力尔特公司的控制器而言,这不是个问题。凌力尔特的控制器通常有内置自适应斜率补偿,以在整个占空比范围内确保电流环路稳定性。LTC3851A 和 LTC3855 是典型的峰值电流模式控制器。
谷值电流模式控制器产生受控 FET 接通时间,并一直等待直到电感器谷值电流达到其谷值限制 (VITH)以才再次接通控制 FET。因此,电源可以在控制 FET 的 TOFF 时间响应负载升高瞬态。此外,既然接通时间是固定的,那么控制 FET 的 TON_min可以比峰值电流模式控制时短,以允许更高的 fSW,实现高降压比应用。谷值电流模式控制不需要额外的斜率补偿就能实现电流环路稳定性。然而,使用谷值电流模式控制时,因为允许开关周期 TS 变化,所以在示波器上,开关节点波形可能出现更大的抖动。LTC3833 和 LTC3838 是典型的谷值电流模式控制器。
为具备闭合电流环路的新功率级建模
图 19 显示,通过仅将电感器作为受放大器 ITH 引脚电压
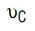
控制的电流源,产生了一个简化、具内部电流环路的降压型转换器功率级的一阶模型。类似方法也可用于其他具电感器电流模式控制的拓扑。这个简单的模型有多好 图 20 显示了该一阶模型和一个更复杂但准确的模型之间转移函数 GCV(s) = vOUT/vC的比较结果。这是一个以 500kHz 开关频率运行的电流模式降压型转换器。在这个例子中,一阶模型直到 10kHz 都是准确的,约为开关频率 fSW 的 1/50。之后,一阶模型的相位曲线就不再准确了。因此这个简化的模型仅对于带宽较小的设计才好用。
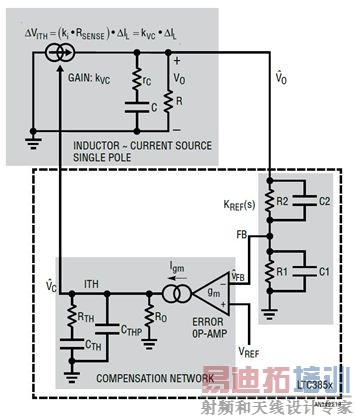
图 19:电流模式降压型转换器的简单一阶模型
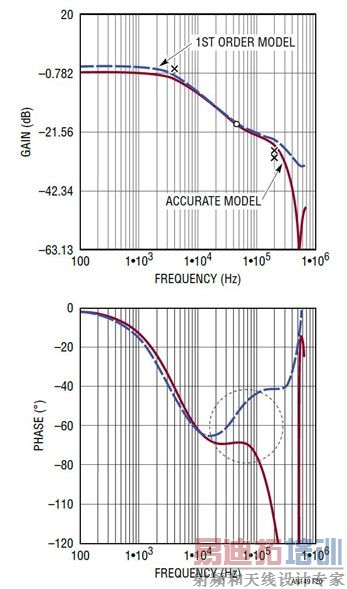
图 20:电流模式降压型转换器的一阶模型和准确模型之间的 GCV(s) 比较
实际上,针对电流模式转换器,在整个频率范围内开发一个准确的小信号模型相当复杂。R. Ridley的电流模式模型 [3] 在电源行业是最流行的一种模型,用于峰值电流模式和谷值电流模式控制。最近,Jian Li 为电流模式控制开发了一种更加直观的电路模型 [4],该模型也可用于其他电流模式控制方法。为了简便易用,LTpowerCAD 设计工具实现了这些准确模型,因此,即使一位经验不足的用户,对 Ridley 或 Jian Li 的模型没有太多了解,也可以非常容易地设计一个电流模式电源。
参考文献
[1] 《Opti-Loop Architecture Reduces Output Capacitance and Improves Transient Response》,
作者:J. Seago,凌力尔特公司《Application Note 76》,1999年5月。
[2] 《Simplified Analysis of PWM Converters Using the Model of the PWM Switch: Parts I and II》,
作者:V. Vorperian,《IEEE Transactions on Aerospace and Electronic Systems》,1990年3月,26卷,第二册。
[3] 《An Accurate and Practical Small Signal Model for Current-Mode Control》,
作者:R. B. Ridley,www.ridleyengineering.com。
[4] 《Current-Mode Control: Modeling and its Digital Application》,作者:J. Li,美国弗吉尼亚理工大学博士论文,2009年4月。
如今的电子系统变得越来越复杂,电源轨和电源数量都在不断增加。为了实现最佳电源解决方案密度、可靠性和成本,系统设计师常常需要自己设计电源解决方案,而不是仅仅使用商用砖式电源。设计和优化高性能开关模式电源正在成为越来越频繁、越来越具挑战性的任务。
电源环路补偿设计常常被看作是一项艰难的任务,对经验不足的电源设计师尤其如此。在实际补偿设计中,为了调整补偿组件的值,常常需要进行无数次迭代。对于一个复杂系统而言,这不仅耗费大量时间,而且也不够准确,因为这类系统的电源带宽和稳定性裕度可能受到几种因素的影响。本应用指南针对开关模式电源及其环路补偿设计,说明了小信号建模的基本概念和方法。本文以降压型转换器作为典型例子,但是这些概念也能适用于其他拓扑。本文还介绍了用户易用的 LTpowerCAD设计工具,以减轻设计及优化负担。
确定问题
一个良好设计的开关模式电源 (SMPS) 必须是没有噪声的,无论从电气还是声学角度来看。欠补偿系统可能导致运行不稳定。不稳定电源的典型症状包括:磁性组件或陶瓷电容器产生可听噪声、开关波形中有抖动、输出电压震荡、功率 FET 过热等等。
不过,除了环路稳定性,还有很多原因可能导致产生不想要的震荡。不幸的是,对于经验不足的电源设计师而言,这些震荡在示波器上看起来完全相同。即使对于经验丰富的工程师,有时确定引起不稳定性的原因也是很困难。图 1 显示了一个不稳定降压型电源的典型输出和开关节点波形。调节环路补偿可能或不可能解决电源不稳定问题,因为有时震荡是由其他因素引起的,例如 PCB 噪声。如果设计师对各种可能性没有了然于胸,那么确定引起运行噪声的潜藏原因可能耗费大量时间,令人非常沮丧。

图 1:一个 “不稳定” 降压型转换器的典型输出电压和开关节点波形
对于开关模式电源转换器而言,例如图 2 所示的 LTC3851 或LTC3833 电流模式降压型电源,一种快速确定运行不稳定是否由环路补偿引起的方法是,在反馈误差放大器输出引脚 (ITH) 和 IC 地之间放置一个 0.1μF 的大型电容器。(或者,就电压模式电源而言,这个电容器可以放置在放大器输出引脚和反馈引脚之间。) 这个 0.1μF 的电容器通常被认为足够大,可以将环路带宽拓展至低频,因此可确保电压环路稳定性。如果用上这个电容器以后,电源变得稳定了,那么问题就有可能用环路补偿解决。

图 2:典型降压型转换器 (LTC3851、LTC3833、LTC3866 等)
过补偿系统通常是稳定的,但是带宽很小,瞬态响应很慢。这样的设计需要过大的输出电容以满足瞬态调节要求,这增大了电源的总体成本和尺寸。图 3 显示了降压型转换器在负载升高 / 降低瞬态时的典型输出电压和电感器电流波形。图 3a 是稳定但带宽 (BW) 很小的过补偿系统的波形,从波形上能看到,在瞬态时有很大的 VOUT 下冲 / 过冲。图 3b 是大带宽、欠补偿系统的波形,其中 VOUT 的下冲 / 过充小得多,但是波形在稳态时不稳定。图 3c 显示了一个设计良好的电源之负载瞬态波形,该电源具备快速和稳定的环路。

(a) 带宽较小但稳定

(b) 带宽较大但不稳定

(c) 具快速和稳定环路的最佳设计
图 3:典型负载瞬态响应 ━ (a) 过补偿系统;(b) 欠补偿系统;(c) 具快速和稳定环路的最佳设计
PWM 转换器功率级的小信号建模
开关模式电源 (SMPS),例如图 4 中的降压型转换器,通常有两种工作模式,采取哪种工作模式取决于其主控开关的接通 / 断开状态。因此,该电源是一个随时间变化的非线性系统。为了用常规线性控制方法分析和设计补偿电路,人们在 SMPS 电路稳态工作点附近,应用针对 SMPS 电路的线性化方法,开发了一种平均式、小信号线性模型。

图 4:降压型 DC/DC 转换器及其在一个开关周期 TS 内的两种工作模式
建模步骤 1:通过在 TS 平均,变成不随时间变化的系统
所有 SMPS 电源拓扑 (包括降压型、升压型或降压/升压型转换器) 都有一个典型的 3 端子 PWM 开关单元,该单元包括有源控制开关 Q 和无源开关 (二极管) D。为了提高效率,二极管 D 可以用同步 FET 代替,代替以后,仍然是一个无源开关。有源端子 “a” 是有源开关端子。无源端子 “p” 是无源开关端子。在转换器中,端子 a 和端子 p 始终连接到电压源,例如降压型转换器中的 VIN 和地。公共端子 “c” 连接至电流源,在降压型转换器中就是电感器。
为了将随时间变化的 SMPS 变成不随时间变化的系统,可以通过将有源开关 Q 变成平均式电流源、以及将无源开关 (二极管) D 变成平均式电压源这种方式,应用 3 端子 PWM 单元平均式建模方法。平均式开关 Q 的电流等于 d ● iL,而平均式开关 D 的电压等于 d ● vap,,如图 5 所示。平均是在一个开关周期 TS 之内进行的。既然电流源和电压源都是两个变量的乘积,那么该系统仍然是非线性系统。

图 5:建模步骤 1:将 3 端子 PWM 开关单元变成平均式电流源和电压源
建模步骤 2:线性AC 小信号建模
下一步是展开变量的乘积以得到线性 AC 小信号模型。例如,变量
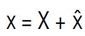
,其中 X 是 DC 稳态的工作点,而
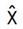
是 AC 小信号围绕 X 的变化。因此,两个变量 x ● y 的积可以重写为:
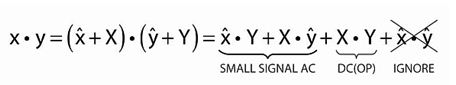
图 6:为线性小信号 AC 部分和 DC 工作点展开两个变量的乘积
图 6 显示,线性小信号 AC 部分可以与 DC 工作点 (OP) 部分分开。两个 AC 小信号变量 (
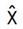
●
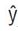
) 的乘积可以忽略,因为这是更加小的变量。按照这一概念,平均式 PWM 开关单元可以重画为如图 7 所示的电路。

图 7:建模步骤 2:通过展开两个变量的乘积给 AC 小信号建模
通过将上述两步建模方法应用到降压型转换器上 (如图 8 所示),该降压型转换器的功率级就可以建模为简单的电压源

,其后跟随的是一个 L/C 二阶滤波器网络。

图 8:将降压型转换器变成平均式、AC 小信号线性电路
以图 8 所示线性电路为基础,既然控制信号是占空比 d,输出信号是 vOUT,那么在频率域,该降压型转换器就可以用占空比至输出的转移函数 Gdv(s) 来描述:

函数 Gdv(s) 显示,该降压型转换器的功率级是一个二阶系统,在频率域有两个极点和一个零点。零点 sZ_ESR 由输出电容器 C 及其 ESR rC 产生。谐振双极点
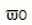
由输出滤波器电感器 L 和电容器 C 产生。
既然极点和零点频率是输出电容器及其 ESR 的函数,那么函数 Gdv(s) 的波德图随所选择电源输出电容器的不同而变化,如图 9 所示。输出电容器的选择对该降压型转换器功率级的小信号特性影响很大。如果该电源使用小型输出电容或 ESR 非常低的输出电容器,那么 ESR 零点频率就可能远远高于谐振极点频率。功率级相位延迟可能接近 –180°。结果,当负压反馈环路闭合时,可能很难补偿该环路。

图 9:COUT 电容器变化导致功率级 Gdv(s) 相位显著变化
升压型转换器的小信号模型
利用同样的 3 端子 PWM 开关单元平均式小信号建模方法,也可以为升压型转换器建模。图 10 显示了怎样为升压型转换器建模,并将其转换为线性 AC 小信号模型电路。

图 10:升压型转换器的 AC 小信号建模电路
升压型转换器功率级的转移函数 Gdv(s) 可从等式 5 中得出。它也是一个二阶系统,具有 L/C 谐振。与降压型转换器不同,升压型转换器除了 COUT ESR 零点,还有一个右半平面零点 (RHPZ) 。该 RHPZ 导致增益升高,但是相位减小 (变负)。等式 6 也显示,这个 RHPZ 随占空比和负载电阻不同而变化。既然占空比是 VIN 的函数,那么升压型转换器功率级的转移函数 Gdv(s) 就随 VIN和负载电流而变。在低 VIN 和大负载 IOUT_MAX时,RHPZ 位于最低频率处,并导致显著的相位滞后。这就使得难以设计带宽很大的升压型转换器。作为一个一般的设计原则,为了确保环路稳定性,人们设计升压型转换器时,限定其带宽低于其最低 RHPZ 频率的 1/10。其他几种拓扑,例如正至负降压 / 升压、反激式 (隔离型降压 / 升压)、SEPIC 和 CUK 转换器,所有都存在不想要的 RHPZ,都不能设计成带宽很大、瞬态响应很快的解决方案。


图 11:升压型转换器功率级小信号占空比至 VO 转移函数随 VIN 和负载而改变
用电压模式控制闭合反馈环路
输出电压可以由闭合的反馈环路系统调节。例如,在图 12 中,当输出电压 VOUT 上升时,反馈电压 VFB 上升,负反馈误差放大器的输出下降,因此占空比 d 下降。结果,VOUT 被拉低,以使 VFB = VREF。误差运算放大器的补偿网络可以是 I 型、II 型或 III 型反馈放大器网络。只有一个控制环路调节 VOUT。这种控制方法称为电压模式控制。凌力尔特公司的 LTC3861 和 LTC3882就是典型的电压模式降压型控制器。

图 12:具闭合电压反馈环路的电压模式降压型转换器方框图
为了优化电压模式 PWM 转换器,如图 13 所示,通常需要一种复杂的 III 型补偿网络,以凭借充足的相位裕度设计一个快速环路。如等式 7 和图 14 所示,这种补偿网络在频率域有 3 个极点和两个零点:低频积分极点 (1/s) 提供高的 DC 增益,以最大限度减小 DC 调节误差,两个零点放置在系统谐振频率 f0 附近,以补偿由功率级的 L 和 C 引起的 –180° 相位延迟,在 fESR 处放置第一个高频极点,以消除 COUT ESR 零点,第二个高频极点放置在想要的带宽 fC 以外,以衰减反馈环路中的开关噪声。III 型补偿相当复杂,因为这种补偿需要 6 个 R/C 值。找到这些值的最佳组合是个非常耗时的任务。

图 13:用于电压模式转换器的 III 型反馈补偿网络


图 14:III 型补偿 A(s) 提供 3 个极点和两个零点,以实现最佳的总体环路增益 TV(s)
为了简化和自动化开关模式电源设计,凌力尔特开发了 LTpowerCAD 设计工具。这工具使环路补偿设计任务变得简单多了。LTpowerCAD 是一款可在 www.linear.com.cn/LTpowerCAD 免费下载的设计工具。该软件帮助用户选择电源解决方案、设计功率级组件以及优化电源效率和环路补偿。如图 15 例子所示,就给定的凌力尔特电压模式控制器而言 (例如 LTC3861),其环路参数可用该设计工具建模。对于一个给定的功率级,用户可以确定极点和零点位置 (频率),然后按照该软件的指导,带入真实的 R/C 值,实时检查总体环路增益和负载瞬态性能。之后,设计方案还可以输出到一个 LTspice 仿真电路上,进行实时仿真。

(a) LTpowerCAD 功率级设计页面

(b) LTpowerCAD 环路补偿和负载瞬态设计页面
图 15:LTpowerCAD 设计工具减轻了电压模式转换器 III 型环路设计的负担
(从 www.linear.com.cn/LTpowerCAD 免费下载)
为电流模式控制增加电流环路
单一环路电压模式控制受到一些限制。这种模式需要相当复杂的 III 型补偿网络。环路性能可能随输出电容器参数及寄生性变化而出现大幅改化,尤其是电容器 ESR 和 PCB 走线阻抗。一个可靠的电源还需要快速过流保护,这就需要一种快速电流检测方法和快速保护比较器。对于需要很多相位并联的大电流解决方案而言,还需要一个额外的电流均分网络 / 环路。
给电压模式转换器增加一个内部电流检测通路和反馈环路,使其变成一个电流模式控制的转换器。图 16 和 17 显示了典型峰值电流模式降压型转换器及其工作方式。内部时钟接通顶端的控制 FET。之后,只要所检测的峰值电感器电流信号达到放大器 ITH 引脚电压 V C,顶端的 FET 就断开。从概念上来看,电流环路使电感器成为一个受控电流源。因此,具闭合电流环路的功率级变成了 1 阶系统,而不是具 L/C 谐振的 2 阶系统。结果,功率级极点引起的相位滞后从 180° 减少为约 90°。相位延迟减少使补偿外部电压环路变得容易多了。相位延迟减少还降低了电源对输出电容器或电感变化的敏感度,如图 18 所示。

图 16:具内部电流环路和外部电压反馈环路的电流模式转换器方框图

图 17:峰值电流模式控制信号波形

图 18:具闭合电流环路的新功率级转移函数 GCV(s)
电感器电流信号可以直接用一个附加的 RSENSE检测,或者间接地通过电感器绕组 DCR 或 FET RDS(ON)检测。电流模式控制还提供其他几项重要的好处。如图 17 所示,既然电感器电流以逐周期方式、通过放大器输出电压检测和限制,那么系统在过载或电感器电流饱和时,就能够更准确和更快速地限制电流。在加电或输入电压瞬态时,电感器浪涌电流也受到了严格控制。当多个转换器 / 相位并联时,通过将放大器 ITH 引脚连到一起,凭借电流模式控制,可以在多个电源之间非常容易地均分电流,从而实现了一个可靠的多项 (PolyPhase) 设计。典型电流模式控制器包括凌力尔特公司的 LTC3851A、LTC3833 和 LTC3855 等。
峰值与谷值电流模式控制方法
图 16 和 17 所示的电流模式控制方法是峰值电感器电流模式控制。转换器以固定开关频率 fSW工作,从而非常容易实现时钟同步和相位交错,尤其是对于并联转换器。然而,如果在控制 FET 栅极关断后,紧接着就发生负载升压瞬态,那么转换器就必须等待一段时间,这段时间等于 FET 断开时间 TOFF,直到下一个时钟周期响应该瞬态为止。这个 TOFF 延迟通常不是问题,但是对于一个真正的快速瞬态系统,它却很重要。此外,控制 FET 的最短接通时间 (TON_min) 不可能非常短,因为电流比较器需要噪声消隐时间以避免错误触发。对于高 VIN/VOUT 降压比应用而言,这限制了最高开关频率 fSW。此外,峰值电流模式控制还需要一定的斜率补偿,以在占空比超过 50% 时保持电流环路稳定。对于凌力尔特公司的控制器而言,这不是个问题。凌力尔特的控制器通常有内置自适应斜率补偿,以在整个占空比范围内确保电流环路稳定性。LTC3851A 和 LTC3855 是典型的峰值电流模式控制器。
谷值电流模式控制器产生受控 FET 接通时间,并一直等待直到电感器谷值电流达到其谷值限制 (VITH)以才再次接通控制 FET。因此,电源可以在控制 FET 的 TOFF 时间响应负载升高瞬态。此外,既然接通时间是固定的,那么控制 FET 的 TON_min可以比峰值电流模式控制时短,以允许更高的 fSW,实现高降压比应用。谷值电流模式控制不需要额外的斜率补偿就能实现电流环路稳定性。然而,使用谷值电流模式控制时,因为允许开关周期 TS 变化,所以在示波器上,开关节点波形可能出现更大的抖动。LTC3833 和 LTC3838 是典型的谷值电流模式控制器。
为具备闭合电流环路的新功率级建模
图 19 显示,通过仅将电感器作为受放大器 ITH 引脚电压
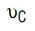
控制的电流源,产生了一个简化、具内部电流环路的降压型转换器功率级的一阶模型。类似方法也可用于其他具电感器电流模式控制的拓扑。这个简单的模型有多好 图 20 显示了该一阶模型和一个更复杂但准确的模型之间转移函数 GCV(s) = vOUT/vC的比较结果。这是一个以 500kHz 开关频率运行的电流模式降压型转换器。在这个例子中,一阶模型直到 10kHz 都是准确的,约为开关频率 fSW 的 1/50。之后,一阶模型的相位曲线就不再准确了。因此这个简化的模型仅对于带宽较小的设计才好用。

图 19:电流模式降压型转换器的简单一阶模型

图 20:电流模式降压型转换器的一阶模型和准确模型之间的 GCV(s) 比较
实际上,针对电流模式转换器,在整个频率范围内开发一个准确的小信号模型相当复杂。R. Ridley的电流模式模型 [3] 在电源行业是最流行的一种模型,用于峰值电流模式和谷值电流模式控制。最近,Jian Li 为电流模式控制开发了一种更加直观的电路模型 [4],该模型也可用于其他电流模式控制方法。为了简便易用,LTpowerCAD 设计工具实现了这些准确模型,因此,即使一位经验不足的用户,对 Ridley 或 Jian Li 的模型没有太多了解,也可以非常容易地设计一个电流模式电源。
参考文献
[1] 《Opti-Loop Architecture Reduces Output Capacitance and Improves Transient Response》,
作者:J. Seago,凌力尔特公司《Application Note 76》,1999年5月。
[2] 《Simplified Analysis of PWM Converters Using the Model of the PWM Switch: Parts I and II》,
作者:V. Vorperian,《IEEE Transactions on Aerospace and Electronic Systems》,1990年3月,26卷,第二册。
[3] 《An Accurate and Practical Small Signal Model for Current-Mode Control》,
作者:R. B. Ridley,www.ridleyengineering.com。
[4] 《Current-Mode Control: Modeling and its Digital Application》,作者:J. Li,美国弗吉尼亚理工大学博士论文,2009年4月。
射频工程师养成培训教程套装,助您快速成为一名优秀射频工程师...
天线设计工程师培训课程套装,资深专家授课,让天线设计不再难...
上一篇:开关电源的建模和环路补偿设计(2):环路补偿设计实例
下一篇:Boost
ZVT-PWM变换器在光伏逆变器中的应用
射频和天线工程师培训课程详情>>

