- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
DC/DC变换器数字PID控制方法研究
录入:edatop.com 点击:
1 引言
随着DSP等数字信号处理器的出现,电力电子电路的数字控制得到了很大的发展。数字处理器能够瞬时读取变换器的输出值,并快速地计算出控制值对变换器进行控制。由于数字控制可以采用灵活的控制策略,一些先进的控制方法应用于电力电子电路成为可能。随着数字处理器价格不断下降和性能的不断提升,应用数字控制的开关型电力变换装置会日益增多。未来电力电子的发展方向可以用“高频化、数字化、绿色化、模块化”来概括。
PID控制是最早发展起来的控制策略之一,由于其算法简单、鲁棒性好及可靠性高,被广泛应用于各种控制中,尤其适合可建立精确数学模型的确定性系统。但实际的电力电子系统是一个线性和非线性相结合的系统,难以建立精确的数学模型。在实际调试过程中,PID参数往往整定不良、性能欠佳,适应性比较差,长期以来,人们一直在寻求数字PID参数的整定方法。本文根据变换器系统的硬件条件将采样频率调至极限值,提高系统的控制性能,运用极点配置的方法整定PID的比例、积分、微分系数,并通过MATLAB仿真修订这些参数,得到良好的控制效果。
2 控制对象简介
本文控制的对象为移相全桥零电压开关变换器。主电路如图1所示。这种变换器结合了零电压准谐振技术和传统PWM变换器技术两者的优点,工作频率固定,在换向过程中利用LC谐振使器件零电压开关,在换向完毕后仍然采用PWM技术传送能量,开关损耗小、可靠性高,是一种适合于大中功率开关电源的软开关电路。
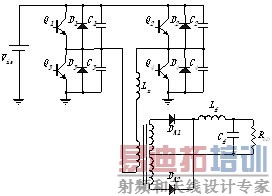
图1 移相控制的全桥变换器
控制器为Motorola公司DSP芯片56F8323,开关频率为150kHz,采用输出电压单环控制,电压环采样频率为25kHz。电压环中,采样输出电压和计算输出电压偏差以及偏差变化,完成电压环的PID计算,同时完成过压保护等功能。计算结果作为移相角大小的依据,实现对变换器的控制。
在这里,为了建立一个形式简单而且不依赖具体负载类型的DC/DC变换器的数学模型做如下一些假设:
①功率开关管是理想的器件;
②LC构成低通滤波器;
③高频变压器为理想变压器;
④考虑开关管的的导通压降、死区效应、线路电阻以及滤波电感的等效串联电阻这些阻尼因素,综合一个等效电阻为r。
3 两种数字PID控制方法比较
数字控制是一种采样控制,它只能根据采样时刻的偏差值计算控制量,因此积分项和微分项需要进行离散化处理。以一系列的采样时刻点kT代表连续时间t,以求和代替积分,以增量代替微分,可以得到离散的位置式PID表达式:
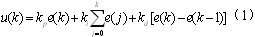
位置式PID控制算法流程如图2所示。
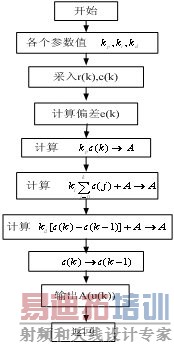
图2 位置式PID控制算法流程图
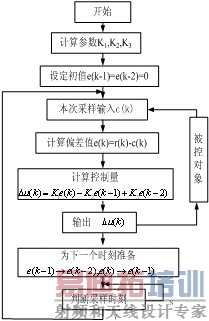
图3 增量式PID控制算法流程图
当执行机构需要控制量的增量,由式(1)可以导出增量式的PID控制算法,见式(2)。增量式PID控制算法流程如图3所示。
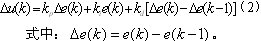
位置式算法是全量输出,每次的输出都与过去的状态有关,计算时要对e(k)进行累加,数字处理器运算量很大。而且,一旦出现问题,控制器的输出幅值会很大,从而导致执行机构大幅度变化,这种情况应该避免。而增量式算法就不存在这个问题,它是增量输出,不需要对过去的状态进行累加,误动作影响小。增量算法也有不足,有静态误差。因此,如果精度要求高、动作比较快的场合用位置算法,如本文电力电子变换器的控制;如果执行的时间比较长,如电机调速控制等,则选择增量式。本文中为了克服位置式算法的缺点,引进抗积分饱和,设置限制范围,避免控制器大幅值的变化。
4 DC/DC变换器数字PID参数整定
4.1采样频率的确定
采样频率在数字控制系统中是一个很重要的参量,从信号保真和控制性能角度看变换器系统的采样频率越高越好。采样频率越高,对硬件要求越高,从而增加硬件的成本。所以选择采样周期应该采取折中的方法选择最佳的采样周期。
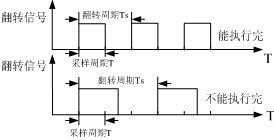
图4 判断程序执行结束示意图
本文的数字控制器选用的是Freescale公司的MC56F8323芯片,主频达到60MHz。为了在现有的硬件条件下确定变换器系统能达到的最大采样频率,在中断程序开始处利用一个通用输入输出端口加以电平翻转指示信号,不断的提高采样频率,根据翻转信号判断中断程序能否执行完,如果指示信号频率小于采样频率的一半,如图4最后一种情况所示,即说明实时中断无法在指定时间内完成,即为现有条件下系统的最大允许采样频率。不同的算法程序,变换器系统能达到的最高采样频率也不一样。
4.2极点配置选择PID参数
数字控制系统,尽管是一个离散系统,如果采样周期T取值足够小,数字控制系统可以近似看作连续系统,对连续系统控制参数进行离散化后,由数字控制器实现变换器的调节。
按照上面的假设,当变换器的LC输出滤波器的截止频率远远小于开关频率,同时直流母线的输入电压Uin恒定不变的时候,移相全桥变换器除了输出滤波器部分可以看成是一个增益恒定的放大器,这一部分的s域模型如图5所示。

图5 移相全桥主电路s域模型
图5中Uab(s)为副边整流后的电压,Uc(s)代表控制器的输出值。这里再设定几个量,iL代表电感电流,io代表的是负载电流,为了分析的方便,io看成是负载的扰动。
考虑移相全桥变换器整流后的输出电压和负载电流的扰动,运用状态空间平均模型法推导输出滤波器的输出响应,见式(3)。同时,可以画出方框图如图6所示。
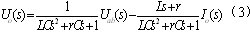
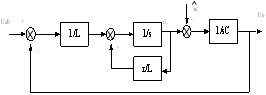
图6 输出滤波器的s域模型
综合主电路、滤波器和PID控制器模型可以得到系统的框图如图7所示。
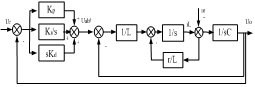
图7 PID控制的DC/DC变换器系统框图
根据图7可以得到系统的闭环传递函数,见式(4)。
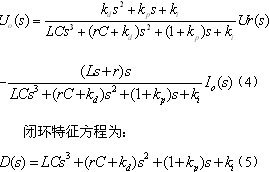
特征方程式(5)的三个根就是系统传递函数的三个闭环极点。闭环系统的动态响应性能、稳定性主要由闭环极点在s平面上分布的位置决定。移相全桥DC/DC变换器的闭环系统是三阶系统,属于高阶系统,其动态特性主要由闭环主导极点决定。如果根据变换器控制系统的动态性能指标确定了闭环系统主导极点希望位于
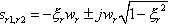
,其中
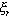
、Wr分别为希望的阻尼比和自然频率,那么系统闭环非主导极点可以选择
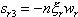
,n为正的常数,n的取值越大,则由三个闭环极点确定的三阶系统响应特性越接近由闭环主导极点决定的二阶系统,一般n=5"10。由此得到满足动态性能要求所希望的闭环系统特征方程为:
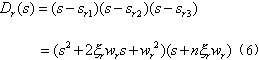
比较式(5)和式(6)可以得到所需参数,该式由极点配置方法得到,所以称为极点配置PID参数公式。
本文的移相全桥DC/DC变换器实际电路的具体参数为:输入Uin=140V"200V,输出U0=24V,输出功率P=220W,输出滤波电感L=20μH,输出滤波电容C=2200μF。以上的模型中,等效电阻r的值很难通过理论分析估计出来,考虑到kp、ki不受r影响,所以根据经验取r=0.264 。确定希望的阻尼比 和自然频率Wr,根据二阶系统的阶跃响应曲线可以知道,阻尼比越小,上升时间短,同时系统的超调量也增大,小到一定程度,系统就会出现振荡。观察 从0"1的阶跃响应曲线发现,阻尼比在0.4"0.8之间为佳,此时单位阶跃响应的快速性和振荡性得到兼顾。根据大量的工程经验, =0.707为最佳阻尼比,所以本文中的 选择0.707。Wr的选取根据阻尼比和系统需要的调节时间来确定,本文Wr选取1600rad/s。根据上述参数得到kp=0.24,ki=1274,kd=0.0000165。
5 仿真与实验结果
本文采用单电压环控制,分别在轻载24W和重载216W时测出稳态的输出电压和输出电流,同时进行24W到216W的突加载实验和216W到24W的突卸载实验。
图8给出在输入电压150V时输出功率为216W时稳态的输出电压电流波形。
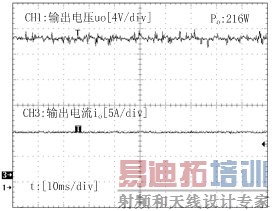
图8 稳态电压电流输出波形
图9为输出功率24W到216W突加负载时的输出电压电流波形,突加负载时电压有4.8V的跌落,超调量为20%,调节时间需要20ms。
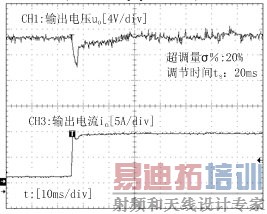
图9 Po:24W→216W电压电流输出波形图
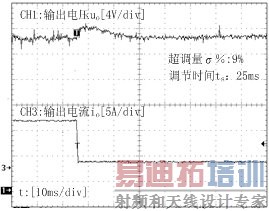
图10 Po:216W→24W电压电流输出波形
图10给出在输入电压150V时输出功率216W到24W突卸负载时的输出电压电流波形,突卸负载时电压有2.16V的过冲,超调量为9%,调节时间需要25ms。
6 结论
实验运行表明,DSP满足位置式的数字PID控制算法的硬件要求,通过测试得到最大采样频率改善系统的控制性能。运用极点配置方法得到的参数满足系统要求,具有良好的静态特性和动态特性。
随着DSP等数字信号处理器的出现,电力电子电路的数字控制得到了很大的发展。数字处理器能够瞬时读取变换器的输出值,并快速地计算出控制值对变换器进行控制。由于数字控制可以采用灵活的控制策略,一些先进的控制方法应用于电力电子电路成为可能。随着数字处理器价格不断下降和性能的不断提升,应用数字控制的开关型电力变换装置会日益增多。未来电力电子的发展方向可以用“高频化、数字化、绿色化、模块化”来概括。
PID控制是最早发展起来的控制策略之一,由于其算法简单、鲁棒性好及可靠性高,被广泛应用于各种控制中,尤其适合可建立精确数学模型的确定性系统。但实际的电力电子系统是一个线性和非线性相结合的系统,难以建立精确的数学模型。在实际调试过程中,PID参数往往整定不良、性能欠佳,适应性比较差,长期以来,人们一直在寻求数字PID参数的整定方法。本文根据变换器系统的硬件条件将采样频率调至极限值,提高系统的控制性能,运用极点配置的方法整定PID的比例、积分、微分系数,并通过MATLAB仿真修订这些参数,得到良好的控制效果。
2 控制对象简介
本文控制的对象为移相全桥零电压开关变换器。主电路如图1所示。这种变换器结合了零电压准谐振技术和传统PWM变换器技术两者的优点,工作频率固定,在换向过程中利用LC谐振使器件零电压开关,在换向完毕后仍然采用PWM技术传送能量,开关损耗小、可靠性高,是一种适合于大中功率开关电源的软开关电路。

图1 移相控制的全桥变换器
控制器为Motorola公司DSP芯片56F8323,开关频率为150kHz,采用输出电压单环控制,电压环采样频率为25kHz。电压环中,采样输出电压和计算输出电压偏差以及偏差变化,完成电压环的PID计算,同时完成过压保护等功能。计算结果作为移相角大小的依据,实现对变换器的控制。
在这里,为了建立一个形式简单而且不依赖具体负载类型的DC/DC变换器的数学模型做如下一些假设:
①功率开关管是理想的器件;
②LC构成低通滤波器;
③高频变压器为理想变压器;
④考虑开关管的的导通压降、死区效应、线路电阻以及滤波电感的等效串联电阻这些阻尼因素,综合一个等效电阻为r。
3 两种数字PID控制方法比较
数字控制是一种采样控制,它只能根据采样时刻的偏差值计算控制量,因此积分项和微分项需要进行离散化处理。以一系列的采样时刻点kT代表连续时间t,以求和代替积分,以增量代替微分,可以得到离散的位置式PID表达式:
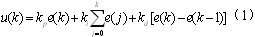
位置式PID控制算法流程如图2所示。

图2 位置式PID控制算法流程图

图3 增量式PID控制算法流程图
当执行机构需要控制量的增量,由式(1)可以导出增量式的PID控制算法,见式(2)。增量式PID控制算法流程如图3所示。
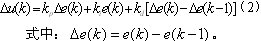
位置式算法是全量输出,每次的输出都与过去的状态有关,计算时要对e(k)进行累加,数字处理器运算量很大。而且,一旦出现问题,控制器的输出幅值会很大,从而导致执行机构大幅度变化,这种情况应该避免。而增量式算法就不存在这个问题,它是增量输出,不需要对过去的状态进行累加,误动作影响小。增量算法也有不足,有静态误差。因此,如果精度要求高、动作比较快的场合用位置算法,如本文电力电子变换器的控制;如果执行的时间比较长,如电机调速控制等,则选择增量式。本文中为了克服位置式算法的缺点,引进抗积分饱和,设置限制范围,避免控制器大幅值的变化。
4 DC/DC变换器数字PID参数整定
4.1采样频率的确定
采样频率在数字控制系统中是一个很重要的参量,从信号保真和控制性能角度看变换器系统的采样频率越高越好。采样频率越高,对硬件要求越高,从而增加硬件的成本。所以选择采样周期应该采取折中的方法选择最佳的采样周期。

图4 判断程序执行结束示意图
本文的数字控制器选用的是Freescale公司的MC56F8323芯片,主频达到60MHz。为了在现有的硬件条件下确定变换器系统能达到的最大采样频率,在中断程序开始处利用一个通用输入输出端口加以电平翻转指示信号,不断的提高采样频率,根据翻转信号判断中断程序能否执行完,如果指示信号频率小于采样频率的一半,如图4最后一种情况所示,即说明实时中断无法在指定时间内完成,即为现有条件下系统的最大允许采样频率。不同的算法程序,变换器系统能达到的最高采样频率也不一样。
4.2极点配置选择PID参数
数字控制系统,尽管是一个离散系统,如果采样周期T取值足够小,数字控制系统可以近似看作连续系统,对连续系统控制参数进行离散化后,由数字控制器实现变换器的调节。
按照上面的假设,当变换器的LC输出滤波器的截止频率远远小于开关频率,同时直流母线的输入电压Uin恒定不变的时候,移相全桥变换器除了输出滤波器部分可以看成是一个增益恒定的放大器,这一部分的s域模型如图5所示。

图5 移相全桥主电路s域模型
图5中Uab(s)为副边整流后的电压,Uc(s)代表控制器的输出值。这里再设定几个量,iL代表电感电流,io代表的是负载电流,为了分析的方便,io看成是负载的扰动。
考虑移相全桥变换器整流后的输出电压和负载电流的扰动,运用状态空间平均模型法推导输出滤波器的输出响应,见式(3)。同时,可以画出方框图如图6所示。
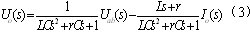

图6 输出滤波器的s域模型
综合主电路、滤波器和PID控制器模型可以得到系统的框图如图7所示。

图7 PID控制的DC/DC变换器系统框图
根据图7可以得到系统的闭环传递函数,见式(4)。
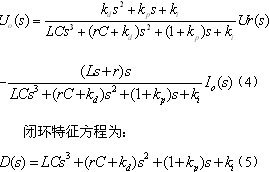
特征方程式(5)的三个根就是系统传递函数的三个闭环极点。闭环系统的动态响应性能、稳定性主要由闭环极点在s平面上分布的位置决定。移相全桥DC/DC变换器的闭环系统是三阶系统,属于高阶系统,其动态特性主要由闭环主导极点决定。如果根据变换器控制系统的动态性能指标确定了闭环系统主导极点希望位于
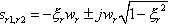
,其中
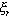
、Wr分别为希望的阻尼比和自然频率,那么系统闭环非主导极点可以选择
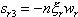
,n为正的常数,n的取值越大,则由三个闭环极点确定的三阶系统响应特性越接近由闭环主导极点决定的二阶系统,一般n=5"10。由此得到满足动态性能要求所希望的闭环系统特征方程为:
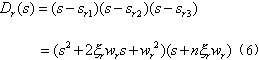
比较式(5)和式(6)可以得到所需参数,该式由极点配置方法得到,所以称为极点配置PID参数公式。
本文的移相全桥DC/DC变换器实际电路的具体参数为:输入Uin=140V"200V,输出U0=24V,输出功率P=220W,输出滤波电感L=20μH,输出滤波电容C=2200μF。以上的模型中,等效电阻r的值很难通过理论分析估计出来,考虑到kp、ki不受r影响,所以根据经验取r=0.264 。确定希望的阻尼比 和自然频率Wr,根据二阶系统的阶跃响应曲线可以知道,阻尼比越小,上升时间短,同时系统的超调量也增大,小到一定程度,系统就会出现振荡。观察 从0"1的阶跃响应曲线发现,阻尼比在0.4"0.8之间为佳,此时单位阶跃响应的快速性和振荡性得到兼顾。根据大量的工程经验, =0.707为最佳阻尼比,所以本文中的 选择0.707。Wr的选取根据阻尼比和系统需要的调节时间来确定,本文Wr选取1600rad/s。根据上述参数得到kp=0.24,ki=1274,kd=0.0000165。
5 仿真与实验结果
本文采用单电压环控制,分别在轻载24W和重载216W时测出稳态的输出电压和输出电流,同时进行24W到216W的突加载实验和216W到24W的突卸载实验。
图8给出在输入电压150V时输出功率为216W时稳态的输出电压电流波形。

图8 稳态电压电流输出波形
图9为输出功率24W到216W突加负载时的输出电压电流波形,突加负载时电压有4.8V的跌落,超调量为20%,调节时间需要20ms。

图9 Po:24W→216W电压电流输出波形图

图10 Po:216W→24W电压电流输出波形
图10给出在输入电压150V时输出功率216W到24W突卸负载时的输出电压电流波形,突卸负载时电压有2.16V的过冲,超调量为9%,调节时间需要25ms。
6 结论
实验运行表明,DSP满足位置式的数字PID控制算法的硬件要求,通过测试得到最大采样频率改善系统的控制性能。运用极点配置方法得到的参数满足系统要求,具有良好的静态特性和动态特性。
射频工程师养成培训教程套装,助您快速成为一名优秀射频工程师...
射频和天线工程师培训课程详情>>

