移相全桥DC/DC变换器动态建模研究

摘要：利用状态空间平均法分析了ZVSPWM睤C/DC变换器主电路并利用状态平均方程对其建立了动态模型，进行了仿真研究。仿真结果证明本方法和研究结果具有一定应用价值。

关键词：移相全桥DC/DC变换器；建模；状态空间平均法

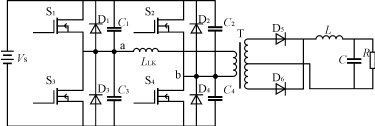
图1FB瞆VS睵WMDC/DC变换器主电路

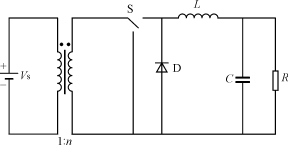
图2典型的Buck电路

1引言

移相全桥零电压开关电路是一种适用于大功率开关电源的软开关电路。它具有电路结构简单，易于实现恒频控制，易于高频化，不需辅助电路，铁磁元件容量小，变压器的漏感和开关器件的寄生电容可以纳入谐振电路，谐振软开关器件应力小，开关损耗小等优点。近年来，移相全桥ZVSPWM睤C/DC变换主电路在DC/DC变换中应用十分普遍。因此，将移相全桥ZVSPWM睤C/DC变换主电路精确建模就显得十分必要。

建立移相全桥ZVSPWM睤C/DC变换主电路的小信号模型的方法很多。本文介绍一种基于状态平均方程的小信号状态空间建模方法。

2小信号模型的建立

移相全桥ZVSPWM睤C/DC变换器主电路拓扑结构如图1所示（图中LLK为输出变压器的漏感）。

移相全桥DC/DC变换电路由Buck电路变化而来，故先分析在变换器的输出电流连续的情况下，基本Buck电路的原理并列写Buck电路的平均状态方程[1]。

典型的Buck电路图如图2所示。

此电路有两种工作状态。即开关S导通状态和开关S关断状态。两种工作状态下的等值电路分别示于图3（a）和图3（b）。

平均状态方程的列写实际上就是将开关器件等效成电路的一个具有增益特性的器件来列写方程。增

(a)导通状态(b)关断状态

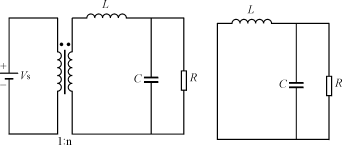
图3Buck电路的两种工作状态

益特性决定于开关在一个周期内的导通时间，导通时间越长，增益越大，最大值为1[3]。结合以上两种开关状态，根据状态空间平均法，有=＋Vs（1）

式中：Vc=Vo，Vo为输出电压，Vc为电容C上的电压；

Vs为输入直流电压；

D为占空比；

iL为电感L上的电流；

n为变压器副边匝数与原边匝数的比值。式（1）为基本Buck电路的状态平均方程。式（1）中，对各变量施加扰动，令各扰动量分别为对应Vs、D、iL、Vo、Vc的扰动分量。注意到各变量对D施加扰动程度是不同的。下面分别讨论各变量的扰动对D的影响。移相全桥ZVSPWM睤C/DC变换主电路与Buck电路不同之处是它存在占空比损失问题，由于移相全桥ZVSPWM睤C/DC变换主电路变压器漏感LLK和变压器副边整流二极管的影响，从S1,S4(或S2,S3)导通到副边电压升到nVs需要一段时间，这就是占空比损失现象。在电路模型中反映出来的是（为有效占空比扰动）的扰动源问题。由于占空比损失，模型中的变压器的变比为1：Deff,，而不是Buck电路中的1：D。

移相全桥ZVSPWM睤C/DC变换主电路波形分析如图4所示[2]。

图4中，vab，iab是图1电路中a，b两点之间的电压和电流。

移相全桥ZVSPWM睤C/DC变换主电路的电压增益可表示为

Vo/Vs=DeffNs/Np=nDeff（2）

式中：Vo为输出电压稳态值；

Ns为变压器副边匝数；

Np为变压器原边匝数。

设ΔD为损失的占空比，则

D=Deff＋ΔD（3）

图4中，当t=t4时，原边电流瞬时值

i3=n(IL－Δi/2)

式中：IL为电感电流平均值；

Δi=i1－i3。

当t=t6时原边电流瞬时值

i2=n[IL＋Δi/2－(1－D)VoT/2L]

式中：T为开关周期。

负载电流i0=V0/R。

根据变换器波形图，可以得出ΔD=(i3＋i2)/（4）

Deff=D－ΔD=D－×[2IL－Vo(1－D)T/2L]（5）

从式（5）可以看出，有效占空比Deff和许多因素有关，不仅跟自身的占空比变化有关，也跟输出电感的电流IL，输入电压Vs有关。由于IL和负载电流i0有必然联系，所以，i0、Vs、D稍有扰动，有效占空比都会产生相应的扰动。假设以上三个扰动量分别为，在Deff上产生相应的扰动分别为、，则（6）

显然，三个扰动分量在Deff上产生的扰动效果是不同的。

将式（5）分别对三个分量取微分，得到Deff对三个扰动的表达式如下：

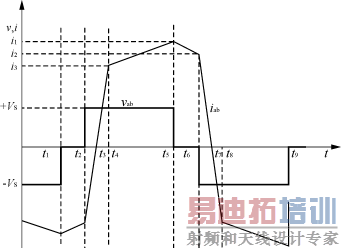
图4主电路波形

[p]
…

()

=－（7）式中：fr为变换频率，且fr=。=(8)=(1－n2Deff)(9)
将各扰动量和相应的静态量的和代入式（1）。由于扰动分量远远小于静态分量，可以认为扰动分量与静态分量的比为无穷小，扰动分量与扰动分量的乘积为无穷小。由此，可以将稳态分量和静态分量分离，得到两组方程。 静态方程：

AX＋BVs=0

V0=FTX（10）

扰动方程：（11）式中：；；；；

式（11）就是移相全桥ZVSPWM睤C/DC变换器的动态低频小信号状态平均方程。为得到该电路的输出对输入占空比的传递函数，将这个状态方程转换为传递函数[2]。将(12)

代入式（11），有：（13）式中：；；。

输入直流电压的波动很小，通常认为是理想的。即=0（14）

将式（14）代入式（13），有（15）

式（15）即为移相全桥ZVSPWM－DC/DC变换电路在输入直流电压稳定不变的条件下的动态低频小信号状态平均方程。简化式（15），得（16）

式（16）即是ZVSPWM－DC/DC变换电路的输出对输入占空比的传递函数。

3模型的稳定性

由电路的稳态条件，Vs=530V，n=0.5，L=0.003H，C=0.0044F，V0=28.5V，LLK=0.003H，fr=10kHz，根据ZVSPWM睤C/DC变换器经常应用于低压大电流输出场合的特点，取R=0.1Ω，模拟大功率大电流负载。

代入式（16），得ZVSPWM睤C/DC变换器的开环传递函数为：（17）

从图5可以看出，相角裕度大于90°，幅值裕度大于80dB，本模型具有较好的稳定性。

4由PI调节器组成闭环控制系统

由PI调节器组成的闭环控制系统如图6所示。图中：M（s）为PI调节器的传递函数；

Fm为脉冲发生器的传递函数；

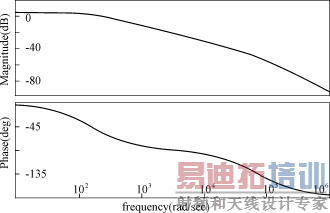
图5动态模型开环Bode图

…

.

.

[p] .

.

.

移相全桥DC/DC变换器动态建模研究

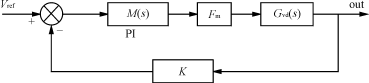
图6系统闭环结构框图

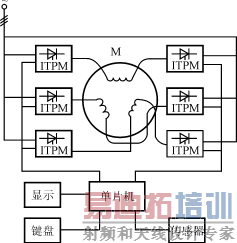
图8负载变化时的输出电压波形

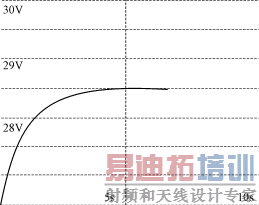
图7输出电压波形

K为反馈放大系数。

根据图6，写出系统的闭环传递函数：（18）式中：为输出电压的拉氏变换；

Vref为输入给定的拉氏变换。

PI环的形式为：M′(s)=Kp＋（19）

式中：Kp为比例系数；

KI为积分系数。 根据劳斯判据，结合系统的超调要求，稳定裕度和调节时间，选取：

Kp=5；KI=6；K=1

5仿真波形分析

PI调节器的参数同上。首先考虑负载恒定，取Vref=28.5V，R=0.1Ω，得到输出电压的仿真波形如图7所示。由图7可见，系统在该负载的条件下，上升时间不足5s，且无超调，具有极好的稳定性。

对于负载变化的情况，采用MATLAB仿真，得到本模型在负载变化时的输出波形，如图8所示。系统带阻性负载，图8表示的负载变化情况为：在t=0时，负载电流为237A,功率为6.77kW；在t=20s时，负载突变至285A，功率为8.1225kW。

从仿真的结果看，在负载突增或突减的情况下，基于状态空间平均法的小信号模型的响应在3～4s内可以达到稳定状态，速度快，且无超调。仿真证明本模型具有良好的稳定性，在大功率大电流的情况下，能够广泛应用。

6结语

本文利用状态平均方程的小信号建模方法分析了移相全桥ZVSPWM睤C/DC变换主电路的模型，着重分析了利用平均状态方程小信号建模方法的建模过程，并得出了移相全桥ZVSPWM睤C/DC变换主电路的小信号数学模型。相对于其它常用的小信号等效电路法，本方法的结果可以直接计算得到，省略了对原电路的小信号处理。相对于不定负载DC/DC建模，本方法的数学表达式虽然精度低一些，但相对简单得多，因而在一般情况下更具实用价值。本方法方程列写方便，数学处理简单且直接从数学分析入手，所用推导都建立在数学理论基础上，易于掌握。通过理论研究和仿真，分析了模型的部分性能，证明本方法和结论可以广泛应用。