基于FPGA的复数浮点协方差矩阵实现

O 引言
协方差矩阵的计算是信号处理领域的典型运算，是实现多级嵌套维纳滤波器、空间谱估计、相干源个数估计以及仿射不变量模式识别的关键部分，广泛应用于雷达、声呐、数字图像处理等领域。采用FPGA(Field Programmable Gate Array)可以提高该类数字信号处理运算的实时性，是算法工程化的重要环节。但是FPGA不适宜对浮点数的处理，对复杂的不规则计算开发起来也比较困难。故目前国内外协方差运算的
FPGA实现都是采用定点运算方式。
在所有运算都是定点运算的情况下，每次乘法之后数据位宽都要扩大一倍。若相乘后的数据继续做加减运算，为了保证数据不溢出，还必须将数据位宽扩展一位，而协方差矩阵的运算核心就是乘累加单元，随着采样点数的增加，位宽扩展呈线性增加。最终导致FPGA器件资源枯竭，无法实现设计。为了保证算法的实现，必须对中间运算数据进行截断，将每次累加的结果除2(可以通过移位运算来实现)，以避免溢出。
此外，在应用MUSIC算法时，各种计算都是复数运算。为达到减少算法的计算量，提高MUSIC算法处理速度的目的，许多文献致力于研究阵列的结构特点，在保证测角精度的前提下，寻找一种简单而有效的数据预处理方法，将复数矩阵转化为实数矩阵，把复矢量用一个实矢量来代替，从而将复数运算转化为实数运算。
接收阵元模型可分为任意离散阵、均匀圆弧阵、均匀圆阵和均匀线阵。在实际应用中，比较常见的是均匀线阵和均匀圆阵。每种阵列模型都有各自的特点，加之阵元数目的取值不同，也会导致阵列流型的对称性变化。针对不同的阵元模型和阵元数，数据预处理的方法也会有所不同。
对于数据预处理的研究，目前已经有了一些比较成熟的算法。对于一个偶数阵元的对称阵列(包括均匀线阵和均匀圆阵)，相关研究表明，可利用其对称性，分成两个完全对称的子阵，选择合适的参考点，构造互为共轭对称的方向矩阵，进而构造一个线性变换矩阵，即可达到将复数矩阵转化为实数矩阵的目的。
对于奇数阵元的均匀线阵，也有相关研究成果表明，通过构造一个酉矩阵，也可以达到数据预处理的目的。
由于均匀圆阵的阵列流型矩阵不是Vandermonde矩阵，即不具备旋转不变性，因此适用于奇数阵元的均匀线阵的预处理理论不能直接用于奇数阵元的均匀圆阵，需要将圆阵先转换到模式空间——虚拟线阵，而转换需要第一类Bessel函数，不适宜用硬件实现。
以上研究表明，目前除了奇数阵元的均匀圆阵外，其他常用阵列模型都可以通过预处理的方法将复数运算转换为实数运算。若在某些特定的情况下，必须采用奇数阵元的均匀圆阵。此时，基于复数运算的协方差矩阵的实现就成为一种必然。
因此，在充分应用FPGA并行处理能力的同时，为了扩展数据处理的动态范围，减少数据溢出机率，避免数据截断所产生的误差，提高协方差矩阵的运算精度以及扩展该运算的通用性。本文以空间谱估计作为研究背景，研究了复数据运算和浮点运算的特点，提出了一种适用于任何阵列流型、任意阵元的基于复数浮点运算的协方差矩阵的FPGA实现方案。

1 求解复数浮点协方差矩阵
以11阵元的均匀圆阵为例，其协方差矩阵的求解方案原理框图如图1所示。

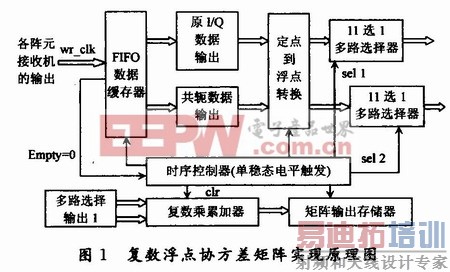
1．1 FIF0数据缓存器
在该设计方案中选择FIFO作为数据存储器，这是因为一旦多路接收机有数据输出，就会启动FIFO进行存储，进而FIFO的不空信号有效(empty=O)，触发后续的矩阵运算；否则，运算停止，一切状态清零，FPGA恢复idle(空闲)状态，等待新的快拍采样数据的到来。
这样可以很方便地控制运算的开始和结束。矩阵运算所需要的同步时钟需要设计一个类似于单稳态触发器的模块。当检测到empty=‘0’时，就触发一个含有121个clk(对于串行方案而言)时钟信号周期长度的高电平。该高电平与主时钟相与便可以得到运算的同步时钟。
1．2 数据共轭转换
由于测向阵列的输出矢量X(t)是一个复矢量，对其求协方差矩阵需用阵列输出列矢量X(t)与其共轭转置矢量XH(n)对应相乘。如式(1)所示：

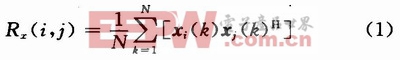
1．3 定点数到浮点数的转换
定点计算在硬件上实现简单，计算速度比浮点计算要快，但是表示操作数的动态范围受到限制，浮点数计算硬件实现比较困难；一次计算花费的时间也远大于定点计算的花费，但是其表示的操作数动态范围大，精度高。在本设计中，考虑到系统的数据动态范围和运算精度，选择浮点计算。由于运算数据是直接从接收机I，Q两路通道的A／D变换器的输出获得，为定点数，因此必须要有一个将A／D采样的定点数据转换为浮点数的过程。设计中将16位定点数转换为IEEE 754标准的单精度格式。32位单精度格式如图2所示，最高位为符号位，其后8位为指数e(用移码表示，基数f=2，偏移量为127)，余下的23位为尾数m。[p]

1．4 浮点复数乘累加器
1．4．1 复数乘法器
假设有两个复数分别为a+jb和c+jd，这两个数的乘积为：

复数乘法器的工作原理如图3所示，其中所用到的加法、减法和乘法器都是基于浮点的运算。值得一提的是，在实现浮点加减法的时候，可以将尾数连同符号位转化为变形补码形式后再进行加减运算。这样做的目的是方便判断数据是否溢出(变形补码判断溢出的规则是：当两位符号位不同时表示溢出，否则无溢出。无论数据是否溢出，第一位符号位永远代表真正的符号)，若溢出，则将尾数右归，指数部分加1，若没有溢出，则将尾数左归(规格化)。浮点乘法相对较简单，对应阶码相加，尾数相乘可以采用定点小数的任何一种乘法运算来完成，只是在限定只取一倍字长时，乘积的若干低位将会丢失，引入误差。

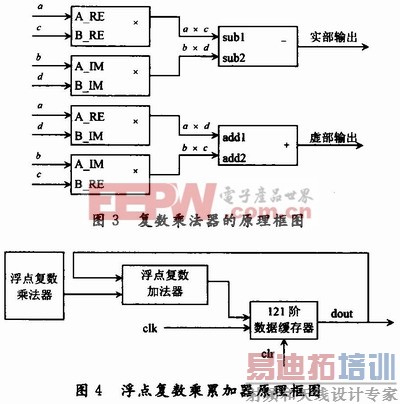
1．4．2 浮点复数乘累加器
以11个阵元的圆阵为例，实现串行处理方案的浮点复数乘累加器的原理如图4所示，实部和虚部(双通道)的乘累加器模块工作原理一样。
121阶数据缓存器实际上就是121个数据锁存器级联形成的一个移位寄存器，初始状态为零。当浮点复数乘法器有输出的时候，启动数据缓存器与之进行加法操作，121个时钟周期以后可以实现一次快拍采样的矩阵累加。累加清零信号由时序控制器给出，当所有的快拍采样点运算都结束之后，数据缓存器输出累加结果(即协方差矩阵的运算结果)，同时控制器送出一个清零信号，清零121阶数据缓存器。

2 仿真结果
可编程逻辑设计有许多内在规律可循，其中一项就是面积和速度的平衡与互换原则。面积和速度是一对对立统一的矛盾体，要求一个设计同时具备设计面积最小，运行频率最高，这是不现实的。于是基于面积优先原则和速度优先原则，本文分别设计了协方差矩阵的串行处理方案和并行处理方案，并用Altera＼stratix＼EP1S20F780C7进行板上调试。其调试结果表明，串行处理方案占用的资源是并行处理方案的1／4，但其运算速度却是后者的11倍。
2．1 串行处理方案仿真结果
如图5所示，clk为运算的总控制时钟；reset为复位控制信号，高电平有效；rd为读使能信号，低电平有效；wr为写使能信号，低电平有效；wr_clk为写时钟信号，上升沿触发；q_clk为读时钟信号，上升沿触发；ab_re(31：O)和ab_im(31：O)为乘法器输出的实部和虚部。q_t2为矩阵乘累加模块的同步时钟信号；clkll，state(3：O)，clkl和state(3：0)是状态机的控制信号，控制矩阵运算规则。

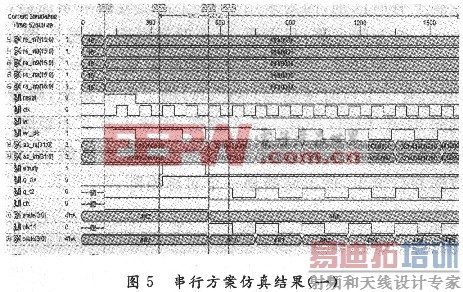
如图5所示，在100 ns时reset信号有效(即reset=‘1’)，所有状态清零。从335～635 ns间，写使能信号有效(wr=‘O’)且有两个写时钟信号的上升沿到来，即向任意一个通道的FIFO中存入两个快拍采样数据，最后输出结果应该有两个矩阵，如图6所示。当FIFO为空时，运算停止，所有状态清零。等待新采样数据的到来。
图5中，在350 ns时，读使能有效(rd=‘0’)且有一个读时钟信号的上升沿到来，所以empty信号存在短暂的不空(empty=‘O’)状态，捕获到这个信息，便触发单稳态触发器模块，产生具有121个clk时钟周期长度，占空比为120：1的q_clk信号，进行FIFO的读操作。[p]
在350～535 ns时间段，因为写时钟信号没有到来，所以FIFO为空(empty=‘1’)。从550 ns～24．75 μs时间段读时钟信号没有上升沿到来，整个设计处于第一个矩阵的运算过程中，即运算一个矩阵所需要的时间为24．2 μs。与此同时，第二个数据写入FIFO，empty一直处于不空状态(empty=‘O’)。
在第一个矩阵运算结束之后，即24．6μs时，系统检测到empty=‘0’，开始读数据并触发第二个矩阵运算的时钟控制信号。如图6所示，在24．6μs时，empty=‘1’。FIFO中的第二个数据被读出，处于空状态。从24．85～49．05μs进入第二个矩阵的运算周期。

在仿真时，输人数据为16位的定点数(1+j1；O+jO；2+j2；3+j3；4+j4；5+j5，6+j6；7+j7；8+j8；9+j9；A+jA)，输出结果为32位的单精度浮点数。选择的主时钟周期为200 ns。在实际调试过程中，整个系统可以在50 MHz主时钟频率下正常工作。
2．2 并行处理方案仿真结果
并行方案运算原理与串行方案的一样，只是在时钟控制上有所区别，因为采用了11个浮点复数乘累加器，进行一次矩阵运算，只需要11个时钟周期，如图7，图8所示。在仿真时，设置在写使能信号有效(wr=‘O’)的同时，有3个写时钟信号(wr_clk)的上升沿到来，即分别向22个FIF0中存入3个数据，则输出有3个矩阵。从图7中还可以清楚地看出，运算结果是矩阵的11行数据并行输出，输出结果是一个对称矩阵。

3 结语
在分析了目前应用于空间谱估计的协方差矩阵运算在硬件实现上的不足，如定点计算的数据动态范围小，运算精度不高，且只适用于特定阵列模型和的阵元数，不具备通用性。在此基础上提出了基于浮点运算的通用型协方差矩阵的实现方案。仿真结果表明，本文所提出的实现方案采用的是复数乘法运算，最终结果得到的是复共轭对称矩阵，适合利用任意的阵列模型和阵元数得到与之相对应的协方差矩阵。这就拓展了协方差矩阵运算的应用范围，且整个运算过程采用的是浮点运算，提高了整个运算的精度。