PCB上信号线产生的电磁频谱

提要：本文主要讨论高速数合逻辑电路中，信号线的电磁发射频谱。作者提供一个模型，其总频谱由两个环路的谐振，即“信号环路”和与基本门电路相关的“旁通环路”控制。

       关键词： PCB，信号线，电磁频谱

在数字电子设备中，PCB板上的元件安装密度越来越高，快速逻辑器件的使用极为频繁。因此，电磁干扰就成为一个极其严重的问题。许多工程技术人员正着手处理这个十分棘手的问题。

如果在产品设计时就考虑EMI问题，那么就会使设计人员省下不少精力，从而进行更加具有创造性工作的研究。在设计阶段找到一条解决EMI问题的途径，这正是本文研究的目的所在。

在电磁兼容问题中有两个主题。一个是电磁发射问题，另一个是电磁抗扰性问题。本文讨论的是数字PCB板上的电磁发射。有许多办法用来预测PCB板的电磁发射。其大多数首先是建立足够精确的数字逻辑电路的等效模型，然后通过大量分析和仿真严格计算PCB上的所有电压或电流波形。这些办法都相当花费时间。

如果电磁发射可由几个截然不同的参数加以特性化，那么就可很容易地进行预测，电磁频谱的包络线由数字电路的谐振决定。本文目的就在于详细探究这些参数，以确定PCB板上上信号线的电磁发射频谱。

如图1所示，PCB板上，可以流动两种瞬态环路电流，两个环路电流都可引起电磁波辐射。一个是IC芯片与其解耦电容组成的环路中流动的电流，作者称之为“旁路回路”。另一个是包括信号线的回路中流动的充电/放电电流。作者称之为“信号回路”。这与后者引起的电磁发射的预测值有关。

图1 PCB上的电流环路

近场EMI的测量

电磁场的特性取决于与源点的距离。在靠近源点处，场强与源电流成正比而与频率无关。另一方面，在源的远处点，场强与频率成正比。作者在PCB上50mm处放置一直径19.4mm的小环形天线，通过测量其感应电压从而求得“近场EMI”的值，测量中的频率扫描范围高达500MHz。

本文中，我们将讨论小环路天线中感应噪声电压的频谱，因为使用的环形天线的敏感性，电压与频率成正比。所以，感应电压的频谱包络线与远场频谱相似。

数字信号线的电磁发射频谱由线谱组成。本文中，我们将讨论仅考虑电磁噪声最坏情况下的频谱包络以及对电路参数发生微小变化很敏感的装置的频谱包络。

在背面铺有地平面的双层PCB板上模拟100mm长的导线，信号线有118Ω左右的阻抗，由74AC系列（74AC00）的CMOS与非门驱动。时钟频率为5MHz。

在建议的工作范围（VGND≤Vin≤VCC），CMOS输入端可以被视为电容。在实验中，信号线通过陶瓷电容接入。

为了确定电磁频谱由两种谐振控制，一种是“旁通环路”的谐振，另一种是“信号环路”的谐振，这里已给出了不同负载电容时测得的频谱。

计算近场EMI的步骤

EMI产生源通常可划分为差模电流与共模电流。本文仅讨论前者。差模发射由电流环路的发射来模拟。环路被分成很短的几部分。每部分均视为一个电偶极子。因此，我们以整个电偶极子来计算信号线的电磁发射。利用计算机计算电磁发射差不多要花10分种左右的时间。

为了计算PCB的电磁发射，需了解PCB上的瞬时电流。这样我们可以按图2的方法在等效电路中运行SPICE。该电路由IC输出模块、信号线和负载电容组成。

IC输出模型是74AC系列的高速CMOS IC的准实验等效模型。因为CMOS输出端设有缓冲级。CMOS门被模拟为串联的转换器。CDS是FET源极与漏极间的寄生电容。因为74AC00中有四个与非门，寄生电容Cp的总值被定义如下：

 CP=4CDS

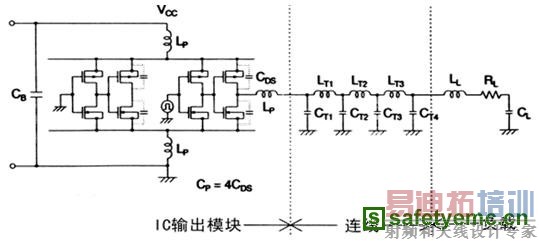
图2 PCB上逻辑电路的等效模型

LP=12.5nH , C=16pF , LT1 =LT2 =LT3=71.4nH/3
CT1= CT4= 5.18pF/6, CT2 = CT3 = 5.18pF/3
LL =15nh, RL =0Ω,CL =6,10,15,20pF

如图2示，在等效电路中，Lp是VCC 、GND或IC输出引脚的电感。

图2中，CB是去耦电容，因为电容CB比寄生电容CP大得多，因此在仿真中去耦电容可以忽略。

电磁频谱在高达500MHz的频率范围内都是可以计算出来的。在频率范围内，可以将信号线视为集总常数电路，因为信号线（=100mm）比波长短。所以信号线被模拟成一系列PI网络。

LT1、LT2和LT3中流动的信号电流被视为PCB中的瞬时电流。

在PCB实验件上，信号线通过陶瓷电容接入。因此，模拟的负载线路如图2所示：CL是负载电容，LL是负载电感，RL是负载电阻。

信号线的电磁发射频谱

本节中，基于前面所述的两个谐振环路的信号线中的电磁发射频谱将予以讨论。

负载电容依从关系

本小节旨在说明在信号线的电磁发射频谱方面，有两个与上述两个谐振回路相关的峰值。

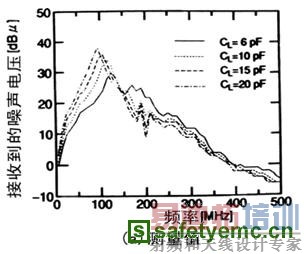
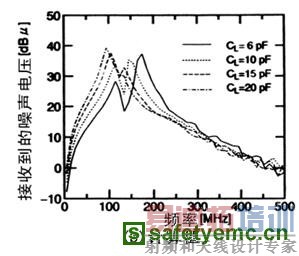
 图3 由负载电容决定的频谱

图3是不同CL时的频谱曲线。图3（a）是100mm的信号线所产生的电磁发射频谱。图3（b）是将其视为图3（a）的“副本”,通过计算得出的频谱。

       图3中，每一负载电容下的频谱均有两个峰值，在CL很大时，每条谱线的肩凸部分被视为第2个峰值。图4中给出了每一峰值的频率。作者称较低的峰值频率为“第2个峰值频率”。根据图4，两个峰值频率均随负载电容CL的增大而降低。第一个峰值频率的计算结果与CL≠6pF时所测得的结果符合。至于第二个峰值频率。计算值与测量近似符合；两者间的最大差值是15MHz。

图4 由负载电容决定的峰值频率;CP=64pF 
 
图5 由寄生电容决定的峰值频率;CL=6pF

    本小节中，我们将讨论如何控制频谱的第一个峰值。为了清楚起见，需模拟不同的寄生电容CP。图5是不同CP值下CL=6pF时计算出的电磁发射峰值频率。根据图5，第一二个峰值频率几乎不随CP的变化而改变。另一方面，第一个峰值频率则随CP变化而变化，因为第一个峰值频率与旁通环路的谐振频率有关。假设“信号环路”与“旁通环路”互不干扰，那么“旁通环路”的谐振频率可由等式（2）给出：  

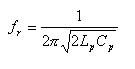(2)   

等式（2）的结果如图5中的实线所示，第一个峰值频率的变化与等式（2）中的fr极为相似。

负载电阻的依从关系

本小节中，讲述第二个峰值出现在频率上的原因。为了探讨这一问题，需在不同负载时同时进行计算和测量。
图6是不同负载时的频谱，图6（a）是100mm长。CL=6pF的信号线所产生的电磁发射的测量频谱。图6（b）是图6（a）“副本”的计算频谱。计算步骤与前面提到的做法完全一样。

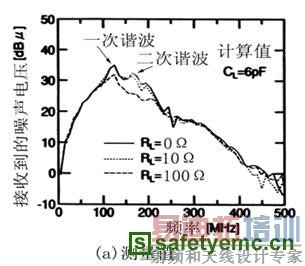
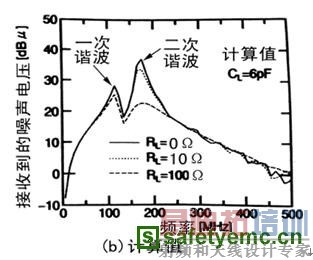
图6 由负载电阻决定的频谱

根据图6，第二个峰值随不同的负载电阻而变化。但第一个峰值则保持不变。第二个峰值取决于谐振“信号环路”的Q因子大小，而第一个峰值则与“信号环路”无关。若RL达到100Ω，则两个峰值都会改变。因为信号线的特征阻抗等于118Ω，当RL-=100Ω，RL可视为串联谐振电阻，因此，振荡电流得以衰减，电流引起的电磁发射被消除掉。

结论

 我们讨论了PCB上信号线产生的电磁发射频谱的峰值频率，电磁频谱取决于两个谐振环路，一个是“旁路环路”，它由IC芯片和去耦电容构成。另一个是“信号环路”，包括信号线在内。

为了预测电磁发射频谱，需要知道其峰值频率和高度。峰值频率可被预测为两个谐振回路的两个谐振频率，峰值高度的预测以后再作讨论。