- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
电磁散射与辐射问题中的混合基函数矩量法
录入：edatop.com 点击：
摘 要：三维散射与辐射问题通常采用电场积分方程（
EFIE）结合矩量法(MoM)求解，而基函数是决定矩量法精度和效率的重要因素。本文针对采用三角形网格剖分会引起未知元过多而采用四边形网格剖分会因为网格质量变差而影响计算精度的问题，提出一种基于三角形与四边形混合网格的混合基函数，应用于散射体RCS和天线阻抗特性计算。结果表明，相比于三角形剖分，混合基函数能够在减少未知元个数的同时获得较高的精度；另外也解决了基于单纯四边形网格的基函数在网格质量较差的情况下不能准确模拟表面电荷的问题。
关键词：混合基函数，电场积分方程，矩量法
1 引言
矩量法是计算电磁学领域中的一种经典方法。早期人们使用线网格（
Wiregrid）模型计算目标电磁特性［1,2］。80年代初，S M Rao等提出了著名的三角屋顶基函数（Triangle Rooftop Basis Functions）［3］。同年，E H Newman等使用平面四边形单元和正弦屋顶基函数也获得了很好的结果［4］，并且在模拟平面散射体时，在相同的精度要求下，它所需要的未知元的个数更少。随着计算机硬件水平的提高以及高速发展的计算机图形学所提供的实体建模与网格生成技术，结合并行算法与快速多极子(FMM)［5］或多层快速多极子算法(MLFMA)［6］的矩量法已经能够解决相当大型的电磁问题。然而矩量法通常要求电尺寸为1/10波长左右的均匀网格，若采用基于传统的三角剖分规则，则生成的网格数目太大；而Paving方法［7］四边形剖分常常不能生成较高
质量的网格，
低质量的四边形网格又会导致对电荷模拟的不准
确。因此企图生成数量少质量高的同种网格来分别适用前述两种基函数以解决电磁问题都有其各自的困难。另外一种情况是研究载体上的天线特性一般要将连接处（
attachment）作单独处理，如果使用四边形单元，已有文献表明在处理上或者不够精确［8］，或者较为复杂［9］，而使用三角形单元则有成熟的算法［10］。这样，我们考虑不妨把两种网格结合起来，发挥各自的长处。Zienkiewica方法［11］在生成四边形网格的过程中会夹杂退化网格（即三角形，如图1所示），但网格质量较高。本文利用这一特点，将定义在不同形状网格单元上的基函数结合起来，建立了一种混合基函数形式，用于复杂形状散射体的RCS计算和金属载体上线天线的输入阻抗计算，达到减少内存并获得较高计算精度的目的。
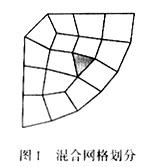
2 EFIE-MoM基本原理
在完全导电的金属物体表面，电场满足：
式中
Ei表示外界的激励，Es表示在激励下的金属表面的感应电流所产生的场，
表示金属表面的单位法向量。而感应电流产生的场又可以用下式表示：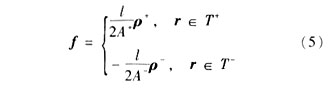
数。k为波数，η为真空中波阻抗。
为了能对复杂的目标进行分析，采用电流的分域基函数展开：
式中
In是展开系数，fn可以是线电流基函数、面电流基函数或线天线与载体连接处的基函数等各种形式。将式(2)代入式(3)，并使用Galerkin法求解，可以得到矩阵方程：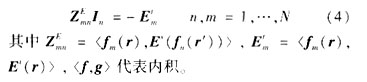
求解方程
(4)，得到电流展开系数，获得金属体表面各处的感应电流密度，进而可求得所需的各种电磁参数。
EMC电磁兼容设计培训套装，视频教程,让您系统学习EMC知识...
射频工程师养成培训教程套装，助您快速成为一名优秀射频工程师...
上一篇：电磁辐射对人眼的危害及防护
下一篇：电子设备测试场中的电磁辐射与防护
