基础电路设计(五)史密斯 表的应用与阻抗整合

前言

印刷电路板的pattern线路有很多必需是借助thruogh hole完成线路路径的布局，对低频电路而言thruogh hole几乎不会对该电路产生不良影响，不过高频电路的阻抗(impedance)整合却扮演关键性角色，换言之若将具有thruogh hole的线路当作一般传输线路处理，就会面临许多超乎预期的困扰，主要原因是在传输线路上如果设有thruogh hole，该部位就会产生非连续性点阻抗，而该点或多或少会形成反射波，最后造成电路误动作，模拟电路的精度发生误差等严重后果。

该反射波的反射程度是用反射系数表示，它是用复素数处理变成复素量。虽然电子电路经常使用复素数与admittance等计算方式，不过实际上复素数计算相当烦琐，其中传输线路与高频电路常用的复素数计算，如果改成史密斯特性图表(Smith chart)方式，就可轻松获得相同的计算结果。有鉴于此，本文将介绍史密斯特性图表(Smith chart)使用上必需注意的事项。
 
　 
反射系数

反射系数是表示整合状态的尺度，反射系数是负载阻抗与传输线路特性阻抗Z₀相异时，部份入射电力未被负载吸收，变成反射电力折返信号源时，入射电力与反射电力的比亦即反射系数可由下式求得:

Γ＝反射波/入射

 
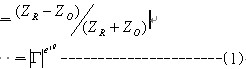
也就是说反射系数是具有大小与位相的量，它可由上式Z_R  与 Z₀ 两个阻抗关系求得，此外式(1)可转换成下式:

【试算例1】
假设传输线路特性阻抗 Z₀  为50Ω，负载阻抗分别是0Ω、50Ω、1kΩ、j50Ω时，反射系数Г=0.5ㄥ45⁰，试算负载阻抗Z_R  。
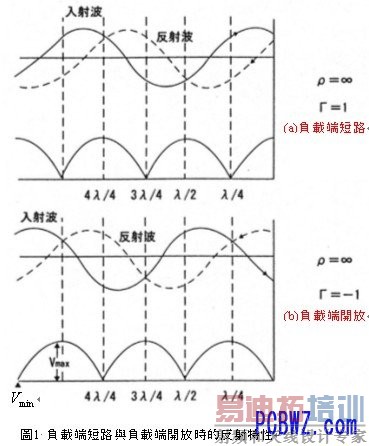
①Z_R=0Ω 时(负载端短路)

这意味着振幅大小相等，位相 180⁰相异的反射波折返信号源，如图1(b)所示。

②Z_R=50Ω 时(整合)
   Г=(50-50)/(50+50)=0
这表示成为整合状态，未发生反射波。

③Z_R=1000Ω 时(不整合)
   Г=(1000-50)/(1000+50)=0.95

④Z_R=∞Ω 时(负载端开放)

这表示振幅大小相等，位相相等的反射波折返信号源，如图1(a)所示。

⑤Z_R=j50Ω 时

⑥Г=0.5ㄥ450时
Z_R=50x[(1+0.5ㄥ45⁰)/(1-5ㄥ45⁰)]
Z_R=50x[(1+0.335+j.355)/(1-0.335-j0.355)]
    =69.07+j65.12(Ω)
由试算例1可知从负载阻抗可求得反射系数的互动关系，反过来说也可由反射系数求得负载阻抗的互动关系，不过若改用史密斯图表方式，就可直接从图表中轻易获得相果。

 　 
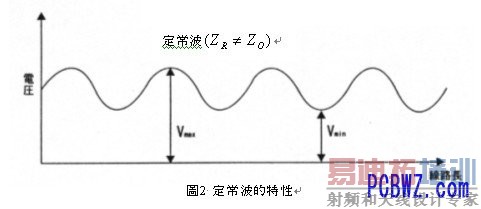
定常波比(VSWR)

定常波比ρ与上述反射系数一样，使用尺度表示整合状态，定长波一旦产生反射波，就会在传输线路上与入射波合成，外观上似乎在传输线路上变成停止状态的波形，波的最大值与最小值的比称赞定在波比ρ，亦即:

此处假设:
①整合(Z_R=Z₀) 时
则式(3)与(4)的反射系数Г=0，定常波比ρ=1 。

②不整合时
不整合时会产生反射波，如果出现如图2所示定在波时，传输线路便具有频率特性。如上所述在高频电路阻抗整合具体重要意义，如果传输线路的特性阻抗Z0 与收
信端(负载)的阻抗相同时，定常波就无法停滞，也就不会有信号传输问题产生，此时的线路可视为无损耗状态，单位长度的特性阻抗在任何位置都是一
定值，因此在形成相同传输线路上，任何位置的波形都与信号源波形的位相都相同，换言之从送信到收信一连串传输线路上的through hole(可能会形成阻抗非连续
点)与信号pattern弯曲部份，必需格外谨慎考虑信号站立时间与线路长度，同时设法避免该部位发生反射现象。