- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
基于Simulink仿真的用户星天线控制系统分析
作者:龙甲禄,闫剑虹
0 引言
伴随着我国中继卫星系统的建立和发展,跟踪与数据中继成为当前航天工程中的一个研究热点,其中一个重要的研究课题是用户星天线对中继星的精确指向跟踪。由于中继卫星系统对天线指向精度要求小于等于0.05°,因此卫星在高精度姿态控制的基础上,还需要增加天线跟踪控制器对天线进行单独控制,才能满足中继卫星系统中星载天线的跟踪指向要求。
星间天线的相互跟踪可以使用程序跟踪方式和自动跟踪方式,由于中继卫星与低轨航天器间传输数据速率高,天线波束宽度窄(Ka频段)只靠程控跟踪实现星间Ka频段天线的相互跟踪,天线指向损失较大,进而对星间链路性能影响较大,所以星间天线常使用自动跟踪模式实现相互跟踪,星间天线的相互自动跟踪主要是由自动角跟踪系统来完成的。
1 天线控制系统的组成
1.1 天线控制系统的指向策略
天线伺服跟踪系统组成如图1所示。
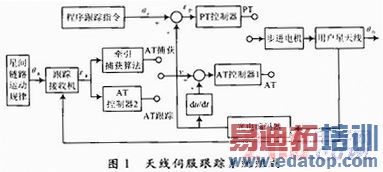
当用户星天线与中继卫星建立联系之前,需要将卫星单址天线指向目标。由于初始偏差很大,卫星根据轨道预报给出的目标轨迹及天线当前的位置,输出控制命令,驱动天线转动,从而使天线在规定的时刻指向预报的正确方向。这一过程称为天线的程控指向模式。
由于卫星轨道预报误差、卫星姿态误差、天线机构及控制等误差的存在,使得天线程控指向角与真实的卫星指向角有一定的偏差,从而造成目标卫星不能出现在跟踪天线的半波束范围内,也就是说,跟踪天线未能捕获目标卫星。为了捕获目标,必须在跟踪天线的指向附近做小范围的扫描搜索,即用户星的捕获牵引模式。
当天线指向与中继卫星视线之间的误差角小于某一给定值,此时跟踪接收机接收到的目标信号达到某一门限值,系统转入自动跟踪模式。在自动跟踪模式下,跟踪接收机通过对天线馈源产生的和信号、差信号进行单通道调制和基带信号处理,完成对接收信号载波频率的捕获跟踪,最后由误差提取电路分离出方位、俯仰误差信号,送往伺服控制单元,驱动天线向误差减小的方向转动,完成自动跟踪。
在用户星天线坐标系内,用户星指向中继星的天线指向方位角和俯仰角与天线电轴夹角的关系为:

终端天线准确指向中继卫星波束时,Ka喇叭只产生和模信号es,当终端天线指向偏离中继卫星新标波束时,将在Ka馈源喇叭中激励起差模信号ed,差模信号中含有方位差信号和俯仰差信号。
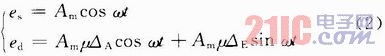
1.2 跟踪接收机
跟踪接收机的任务就是从输入和信号es与差信号ed中,检测出方位误差和俯仰误差的电压值。
和、差信号分别经过低噪声放大K∑,K△后,再对差信号进行四相调制,然后合成一路信号:

合成信号经过下变频至中频,中频信号经过放大,AGC调整后,对中频信号进行相干解调,经过检波滤除直流分量可得:
![]()
在设备调试时,应调整和、差信号合成前和差信道的相对相位差接近为零,即α=0,又因为△A=θcosφ,△E=θsinφ,在四相调制的一个周期内,根据β(t)的不同取值有:

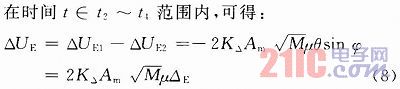
该值就是系统完成闭环所需的方位误差和俯仰误差的电压值。
图2为信噪比10 dB下跟踪接收机的阶跃响应。为了便于观察,设定θ=0.4,φ=0,则由式(1)、式(7)和式(8)可知,输出方位误差信号变化与θ一致,俯仰误差信号为零。可以看出,跟踪接收机输出的方位、俯仰误差信号与方位、俯仰角不是一个准确的线性关系,误差信号存在延时和干扰信息。

1.3 二相混合式步进电机
混合式步进电动机具有步距角较小,分辨率高,控制电流小,功耗低等优点,作为控制用电动机和驱动用电动机广泛应用于工业领域。在用户星天线跟踪控制系统中,根据系统性能指标和星上环境要求,选择二相混合式步进电机作为控制系统的执行元件。
对于二相混合步进电机,在不计定子极间和端部的漏磁,不计永磁体回路的漏磁,忽略磁滞和涡流的影响,忽略饱和的影响,忽略定子线圈自感的谐波分量,且绕组自感及绕组间互感不随转子机械角的变化而变化,步进电机的数学模型可以描述为:
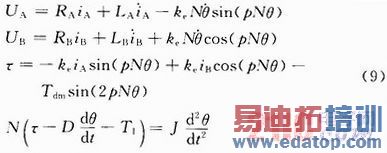
这里谐波减速器简化为一个减速比为N的刚性环节,并把负载转动惯量向驱动端折算。式中,UA,UB分别表示施加在A相、B相绕组两端的电压;iA为A相电流,iB为B相电流;LA为A相电感,LB为B相电感;τ为变化的转矩;p是转子齿数;ke为转矩常数;Tdm为静态转矩;J为转动惯量,包括转子转动惯量和负载等效转动惯量;D为粘性摩擦系数;Ddθ/dt是包括风损、机械损在内的摩擦转矩,它也包含磁滞涡流所致的二次电磁效应;T1为负载转矩;θ为电机输出角度。
为满足天线控制系统高稳定性和高可靠性的要求,选用的驱动主电路结构是H桥电路,驱动方式为斩波恒流驱动和电流细分驱动。为了使二相混合步进电机有恒定转矩的输出,需要精确控制绕组电流,在驱动电路中引入电流闭环,这样就可以实现精确的电流控制。电流控制器根据绕组实际电流和给定电流的差值,通过H桥实现电流斩波控制,输出绕组电压信号。本文驱动方式采用带有电流细分的斩波恒流驱动,给定绕组电流为:
![]()
式中:im为给定电流最大值:k为转子步数;,n为细分数。
图3为二相混合式步进电机的阶跃响应。可以看出,输出在平衡位置有轻微的抖动,这是因为步进电机是以离散的方式运行的,所以电机的步进角即为电机的最小前进角度,因此可能电机无法完全运行到给定位置,造成了转子在平衡位置来回震荡。

2 仿真分析
根据前面的分析,在Simulink里面建立了天线控制系统的仿真模型,如图4所示,控制器采用速度PID控制,当角度偏差较大时,则转速也随之增大,电机以限定的最高转速运行,使得位置偏差减小,这样可以提高系统的输出特性。控制器参数kp=1.2,kI=0.004。
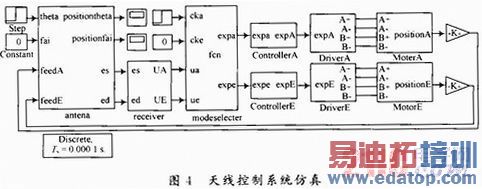
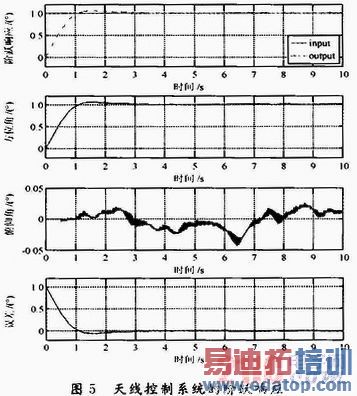
图5为天线控制系统的阶跃响应,可以看出,在接收机输出信号干扰较大的情况下,天线控制系统能较好地跟随目标。方位轴角度变化与θ一致,俯仰轴角度在零值附近,天线转动角度能跟随给定θ,说明所建立的仿真模型能实现天线控制系统的功能。在初始角度偏差较大时,模式选择模块选择程控模式,控制器作用电机以限定的最高转速运行,使偏差快速减小。当角度误差小于0.4°时,牵引转入自动跟踪模式,控制器根据接收机输出的方位、俯仰误差电压控制电机转速增大或减小,使偏差进一步减小,最终达到稳定状态,稳态时的跟踪误差低于0.05°。
天线控制系统要求跟踪精度低于0.05°,因此给定输入为斜坡信号,角速度为0.25(°)/s,系统的输出响应及误差曲线如图6所示。
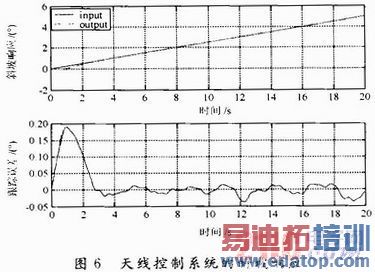
从图6可以看出,系统稳定时的跟踪误差低于0.05°,满足天线控制系统的指向精度要求。
3 结语
在对天线控制系统各组成部分进行分析的基础上,在Simulink环境下完成了天线控制系统的仿真模型,所搭建的仿真模型能实现天线控制系统的各个功能,并能准确地跟随目标,跟踪误差低于0.05°,满足天线控制系统的指向精度要求,证明了所设计的天线指向控制系统的有效性,为进一步研究天线控制系统的抗干扰性能提供了基础。


