- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
磁致位移传感器检测线圈与信号振荡关系研究
1、引言
细长直线磁致伸缩传感器是利用磁致伸缩材料的磁致伸缩效应实现的一种绝对式位移传感器,主要用于距离测量领域,如:液位测量、水位监测等领域,尤其是易燃易爆、易挥发、有腐蚀的环境中[1]。
该种传感器通过检测线圈来监测磁致伸缩直线上磁畴变化引起的磁通量的变化,并通过相应的时间计算得出实测点的位移。按照引起磁通量变化的主要影响因素可将线圈检测到的电压波形分为感应波形和弹性波形两种,其中,感应波是由传感器系统驱动脉冲电流发生时,在磁致伸缩线体材料上产生的周向磁场作用下,磁致伸缩材料发生磁化和磁致伸缩变化引起的;弹性波形是在磁致伸缩效应作用下磁致伸缩线体材料中产生了的扭转式超声波,当扭转波到达检测线圈位置时,磁性材料在逆磁致伸缩效应下产生的[2]。
首先,感应波信号较弹性波信号强许多,相对容易检测和分析;其次,感应波影响因素相对较少,易于给出相应的理论分析和解释;第三,感应波发生时,磁致伸缩材料发生的物理变化是产生弹性波的直接原因,对感应波的机理研究将对研究弹性波有着重要的意义。
作者对传感器系统中的感应波进行了多种方案的检测,分析了感应波波形中振荡发生的主要原因,对检测线圈匝数与感应波的波形信号关系进行了实验分析和理论探讨,为该种传感器检测系统的设计及线圈参数的确定提供了理论依据和实验数据。
2、细长直线磁致传感器基本原理
磁致伸缩传感器基本工作原理如图1所示。
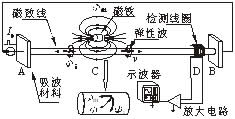
图1 磁致伸缩直线传感器基本工作原理图
当给磁致伸缩线加以脉冲电流Ip时,线的附近便会产生周向磁场Фi;另一方面,在该线附近的永久磁铁会引发轴向磁场Фm。当脉冲电流Ip流过磁致伸缩线时,两磁场Фi和Фm合成一个瞬间扭转磁场Ф。由于磁致伸缩效应,导致合成磁场处的磁致伸缩线发生瞬间形变,进而产生弹性波,并沿轴向以一定的速度v向线的两端传播。
由于磁致伸缩线体材料的长度L远远大于直径D,则在计算周向磁场时可将线体假设为无限长。如图1所示,在线的一端设有检测线圈,当加载脉冲电流Ip时,载流无限长直导线周围的磁感应强度B为:
B=(μ0I)/(2πr0) (1)
在此磁场作用下,检测线圈覆盖的线体材料中的磁畴发生偏转和磁畴壁的位移,改变了轴向磁通量的大小,在检测线圈中便产生电压波形,在此称为感应波形。当扭转波到达检测线圈时,由于机械应力的改变,在逆磁致伸缩效应的作用下,线体中的磁畴发生变化引起轴向磁通量发生变化,在线圈中产生电压波形,称为弹性波形。
根据法拉第电磁感应定律,当检测线圈轴向发生磁能量改变时,在线圈两端便产生感应电动势e,其大小如(2)式所示。
e=-NS(əB/ət) (2)
式中 e:感应电压 [V];N:检测线圈的匝数;S:检测线圈金属线横截面积 [m2];B:磁通密度 [T]。由于əB/ət也是随时间变化的量,所以,e是t的函数。
位移的检测是通过计算弹性波从磁铁到检测线圈之间的传播时间t来实现的,设弹性波的传播速度为v,则永久磁铁到线圈的距离L如(3)式所示[3]。
L=vt (3)
由图1及磁致伸缩传感器原理可知,不仅弹性波对检测信号有影响,而且感应波对检测信号也有影响;在实际工作系统中,影响检测信号的还应有周向磁场直接对线圈的影响、环境磁场对线圈的影响、各种环境电磁波信号对线圈的影响以及线圈及附属检测系统电路自身的电气特性对信号的影响。
3、检测线圈与检测信号
作者采用不同匝数的检测线圈,对感应波信号进行了检测,检测线辊相关技术参数如图2所示,检测结果如图3所示。可以看出,随着检测线圈匝数的增加,感应波振幅变大,周期变长。
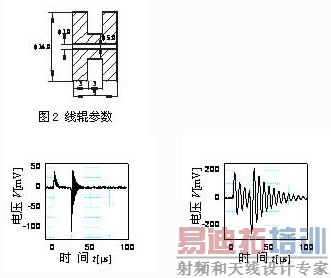
(a) 200匝 (b) 1000匝
图3 不同匝数线圈检测到的感应波形
图4为不同匝数线圈检测到的感应波形的峰峰值变化,及第一个尖峰值的变化。
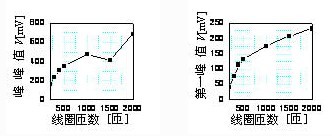
(a) 峰峰值 (b) 第一峰值
图4 不同匝数线圈检测到的峰值
由图3和图4可知,在驱动脉冲电流的脉冲方波作用下,脉冲方波的前沿(上升沿)在线圈中产生正向的振荡波形,本文称之为前沿振荡;脉冲方波的后沿(下降沿)在线圈中产生负向的振荡波形本文称为后沿振荡,它们有以下特点:
① 感应波波形发生了两次变化,其中一次发生在驱动脉冲方波的前沿(上升沿),一次发生在后沿(下降沿);② 随着线圈匝数的不断增加,前沿振荡和后沿振荡的振幅不断增大,周期也不断变长;③ 振荡的影响时间随线圈匝数的增加而变长,直到前沿振荡和后沿振荡交织在一起,当交织的前沿振荡与后沿振荡相位一致时峰峰值变大,当前沿振荡与后沿振荡相位相反时峰峰值变小;④由第一峰值的变化可知,随着线圈匝数的不断增加,第一峰值不断变大。
本文对不同匝数线圈检测到的感应波进行了频谱分析,随线圈匝数的变化感应波周期及频率变化如图5、图6所示。

图5 线圈匝数与周期的关系 图6 线圈匝数与频率的关系
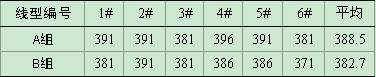
而对同匝线圈不同线体材料进行测试时,感应波主频基本一致,如表1所示。表中所示数据是采用500匝检测线圈,对六种线体材料、两种初始化方案下进行的感应波检测和主频分析。由表可知,在线圈匝数为500匝时,所检测到的感应波形的振荡频率基本保持在386kHz附近。
以上实验表明:不同磁致伸缩线体在同匝检测线圈方案下进行检测时,材料的变化未引起感应波主频率的较大变化。
表1 同匝异线感应波频率分析结果(kHz)
4、信号振荡与线圈匝数关系的分析
由于影响线圈信号的因素较多,本文对感应波信号振荡的主要影响因素进行了分析。
首先,所检测到的感应波的振荡不应是磁畴偏转振荡的直接反映。由式(1)可知:当电流呈方波波形时,周向磁场随时间的变化亦呈方波波形。如图7所示[4],如果周向磁场引起的是可逆磁畴变化,磁通量应为O状态对应的磁畴磁通量或A状态对应的磁畴磁通量;如果周向磁场引起的是不可逆磁畴变化,磁通量应为B状态对应的磁畴磁通量或C状态对应的磁畴磁通量。而在定磁场作用下,磁畴将保持一种固定的状态,或在该状态附近。另外,在驱动脉冲电路一定的情况下,驱动脉冲的前沿振荡和后沿振荡是一定的,磁畴即使随驱动脉冲的前沿振荡和后沿振荡波动,其主频值也不会因检测线圈匝数的变化而变化[5-6]。所以,通过线圈检测到的振荡不应该是磁畴偏转振荡的直接反映。
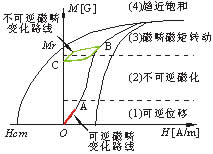
图7 磁化和反磁化过程的各个阶段
其次,所检测到的感应波的振荡不应是由磁致伸缩线体的振荡变化引起的。分析如下:若振荡是由磁致伸缩直线扭转导致的逆磁致伸缩效应引起的磁通量的变化,则:对于相同的磁致伸缩线体,当采用不同的线圈匝数进行检测时,感应波振荡频率不应有较大的变化;对于不同的磁致伸缩线体,采用相同的线圈匝数进行检测时,感应波振荡频率应有较大的差异。而这与实验结果不符。
反之,由实验结果可知,感应波振荡的原因应主要是检测线圈电路的电信号振荡。作者对感应波振荡频率与检测线圈匝数的关系进行理论分析。
理论上,自感系数的计算方法一般比较复杂,实际中常常采用实验方法来测定,简单的情形可以根据毕奥-萨伐尔定律和式(4)进行计算:
Ψ=LI (4)
其中Ψ是磁通匝链数,L是自感系统,I是电流。
对于单匝密绕螺线管有:
L=μ0n2V=μ0N2S/l (5)
其中μ0是真空磁导率,n是单位长度内的匝数,V是螺线管的体积,N是总匝数,S是螺线管的截面积,l是螺线管的长度。
由RLC电路暂态过程相关理论,针对如图8所示的理想电路,对于电路中的振荡信号讨论如下。
图8 LCR电路
电路中的阻尼度为:
![]() (6)
(6)
如果电路中的电阻不太大使得λ<1,便可视为阻尼振荡,其振荡频率f和周期T在L>>R时有:
![]() (7)
(7)
![]() (8)
(8)
由公式(5)、(7)、(8)可得:
![]() (9)
(9)
![]() (10)
(10)
对于本文所讨论的线圈,在匝数N变化时,截面积S和分布电容C也会发生变化。由前述实验可知,引起感应波信号振荡的主要因素应为检测线圈本身,当截面积S和分布电容C随线圈匝数变化较小时可近似为常量,此时即有:感应波信号振荡频率与线圈匝数成反比关系,感应波信号振荡周期与线圈匝数成正比关系。
5、结论
本文通过实验确定了在通过检测线圈检测磁致伸缩直线位移传感器的信号波形时,所得到的波形主要是感应波形和弹性波形,其中引起感应波的主要是磁致伸缩效应下磁畴的偏转和磁畴壁的位移,但感应波信号的前沿振荡和后沿振荡并不是磁畴变化的直接反映,而是与检测线圈匝数有关的量。分析可知,感应波信号振荡频率与线圈匝数成反比关系。该结论为进一步提高传感器系统的检测精度和检测范围,规避检测线圈对检测信号的负面影响,提供了实验数据和理论基础。
参考文献
[1] 黄卉,肖定国,理华,等.磁致伸缩式扭转超声波位移传感器的研究与设计[J].仪表技术与传感器. 2002.6: 4-5.
[2] 伍艮常,磁致伸缩式液位传感器[J], 仪表技术与传感器, 2007.12:9-11
[3] Fernando Seco, José Miguel Martín, José Luis Pons, et al. Hysteresis compensation in a magnetostrictive linear position sensor [J]. Sensors and Actuators A.2004.110: 247-253.
[4] 钟文定.铁磁学(中册) [M].北京:科学出版社.1987.
[5] KUZ’ MENKO A P, ZH UKOV E A. Magneto-elastic waves in the orthoferrite plates induced by solitary domain wall [J]. RARE METALS. 2007.26:5-9
[6] 周浩淼. 铁磁材料非线性磁弹性耦合理论及其在超磁致伸缩智能材料中的应用[D].兰州大学.2007.
上一篇:工程师,你所不知道的功率测量最简易方法
下一篇:测量仪表设计关键之数据采集(一)


