- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
电力电子电路健康监测的特征参数选取和阈值建立
摘要:文中提出的是关于电力电子电路健康监测的特征参数选取和健康阈值确定的方法。该方法以到健康样本集的马氏距离为特征参数,以正态化马氏距离的均值和均方差构建健康阈值。本文以Buck电路为例,选择电路输出电压作为监测信号,提取输出电压平均值及纹波值作为关键参数,计算马氏距离作为特征参数,求得健康阈值。然后用这些数据实现电路的健康状态监测。实验结果表明,利用该方法能够跟踪故障关键参数的变化趋势,有效实现电力电子电路的健康监测。
关键词:电力电子电路;健康监测;特征性能参数;马氏距离;健康阈值
电力电子电路在大型设备的健康预测和管理系统(PHM)中是比较重要的一个部分,也是很多设备正常运转的基础。因此,对电力电子电路健康监测研究具有非常重要的理论意义和应用前景。而特征参数的选取和健康阈值的建立,对电力电子电路的健康监测十分重要。
电路的变化是一种渐变的退化。文中试图通过对电路关键参数的监控,把握这种变化趋势,实现电路健康状态监测。验证或实现该监测方法的基本思路是:测得健康产品的健康样本集后,以电路元件的渐变退化测试电路输出电压的变化情况。若存在某种趋势,则判断该趋势的某一状态后电路是否都处于故障状态。由此可监测电路的健康状态。
文中以Buck电路为例,主要工作是求得特征参数马氏距离、以正态化马氏距离的均值和均方差构建健康阈值、用ESR、L、C这3个参数进行实验,监测电路的健康状态。这是一种基于概率的方法。实例中将Buck电路的健康指标——输出电压均值和纹波转换成马氏距离,考虑正态化后的马氏距离偏离程度来判断电路的状态,使判别更为科学化。
1 电力电子电路健康监测的方法和流程
电力电子电路健康监测的具体步骤为:1)确定输出电压的均值和纹波为关键参数,仿真健康系统,测得健康样本集;2)求得健康样本向量对于健康样本集的马氏距离(MD),以该马氏距离为特征参数;3)对特征参数马氏距离进行正态化,求得正态分布的均值的方差,构建健康阈值;4)测得待测试样本的关键参数集,求得MD,进行正态化。5)将该正态化后的MD值与健康阈值比较,确定电路的健康状态。流程如图1所示。
作为特征性能参数,能较好地进行故障诊断和预测。本文则将这两个参数转化为对健康样本集的马氏距离(MD)来进行统一衡量。所求得的马氏距离就是我们选定的特征性能参数。选择马氏距离作为特征参数有这几个优势:1)对多个分量可以进行统一衡量,不用每个分量都去算一次;2)可以消除分量间的相关性造成的影响;3)采样一种概率检测故障的方法,减少人为的误差。
1.1.2 特征性能参数马氏距离(MD)的计算
1)求输出电压平均值。对一定周期进行采样,求得输出电压平均值。
2)求纹波电压。纹波电压是指输出电压的交流分量,可以用有效值或峰值表示。文中选择峰一峰值表示纹波的大小。监测稳态时电路输出电压,得到输出电压的波形数据,提取其最大、最小值,两者之差即为纹波电压的峰-峰值。
3)马氏距离(MD)
马氏距离(Mahalanobis Distance)是由印度统计学家马哈拉诺比斯(P.C.Mahalanobis)提出的,表示数据的协方差距离。它可以有效的计算一个样本和一个样本集“重心”的距离,或者计算2个位置样本集的相似度。它的优点是不受量纲影响,能体现各个参数之间的联系并排除相关性于扰。
在计算马氏距离的时候,要求总样本数大于样本的维数。否则得到的总体样本协方差矩阵逆矩阵不存在,导致马氏距离无法计算。
1.2 健康阈值
1.2.1 BOX-COX变换
马氏距离总是非负的,但它们一般不服从正态分布。Box-Cox的幂变换可以用来把正的但不服从正态分布的变量转换成正态分布。本文将通过Box-Cox变换将马氏距离转化为正态分布。
1.2.2 健康阈值的计算
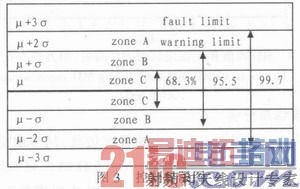
对马氏距离正态化之后,计算该正态分布数组的均值μx和均方差σx,可得到一个通用的健康阈值。对于一个正态分布数组,数据落到2σx之外的概率为5%,落到3σx之外的概率很小,仅为0.3%。如果一个测试数据落在3σx之外,可以认为该数据异常。文中选择阈值(μx+ 2σx)为预警线,阈值(μx+3σx)为故障线,用于区分测试数据对正常样本的异常程度。该阈值可画成控制界限图。如图3所示。通过控制界限图可以方便地进行电路健康状态监测。
1.3 电力电子电路健康状态判别方法
将向量组(u,△u)转换成对健康样本集的马氏距离MD,再通过Box-Cox变换把MD转换成正态分布X。通过计算X的均值μx和均方差σx,构建出如图3所示的控制界限图。
检测电路故障的原则是:第一,对于一个样本,当代表该样本的点落到故障线之外(即阈值μx+3σx)即是故障样本。第二,对于一组相同故障元件的样本,可以选择一个落到故障线外的点的统计值(比如95%以上的点落在故障线之外)来检测故障。该方法的优点是:有明确的虚警率,为0.3%;可以调整检测误差。此外,越高的MD表示越接近于故障,控制图中越靠近上方的点对于识别系统健康的变化十分重要。文中采用蒙特卡洛的方法仿真多组同状态Buck电路进行故障检测,当有95%以上的点落在故障线以外,说明输出电压的均值或者纹波偏离过大,Buck电路发生故障。
2 电力电子电路健康监测实例及结果分析
2.1 电力电子电路健康监测实例
以图2所示Buck电路为例。其中ESR(0)=0.495 Ω;ESR、L和C均取容差为18%。使用Pspice软件做600次高斯分布的蒙特卡洛仿真分析,相当于选取600个健康的Buck电路进行检测。监测输出电压Uo并获取稳态时的波形数据。然后,在Matlab10.5环境下编程计算输出电压的平均值和纹波值(u,△u)矩阵,所得即为健康样本集。计算每个向量(u,△u)对健康样本集的马氏距离,所得MD值为特征参数。对MD进行Box-Cox变化,得到健康阈值并构建控制界限图。
假定其余参数不变化,分别选取ESR、电容、电感进行渐变仿真,测得电压均值和纹波的样本集后,求得该测试样本集到健康样本集的MD值并进行Box-Cox变化,再与健康阈值进行比较。这样就能较好的监控到单个元件退化对输出的影响,及输出电压的变化趋势。
2.2 实验结果分析
测试样本按照图1所示电路设置仿真,只考虑ESR渐变退化。图4和表1显示的是ESR从0.5 Ω增大到1.5 Ω、每隔0.1 Ω进行一次测试的测试结果。L、C均取容差为18%,每个测试点做100次高斯分布的蒙特卡洛仿真。MD均值和正态化后的MD均值、均方差变化情况如图4。显然,特征参数MD值和正态化后的MD值分布是递增的,但增长速度逐渐下降;正态化后的MD均方差大致是减小的。MD值分布的递增性质说明能够对电路的关键参数进行有效跟踪,监测电路的健康状态。
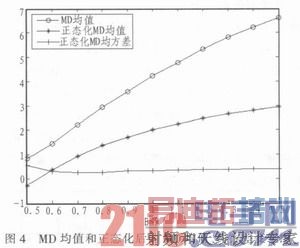
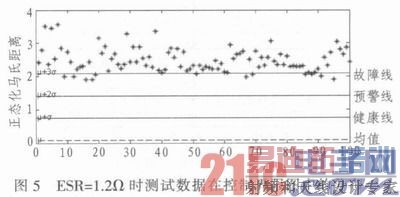
表1显示随着ESR增大时,电压均值、纹波和特征参数的变化情况。“溢出率”是指测试数据超出故障线(即阈值μx+3σx)占该测试点测试样本的比率,图5显示测试数据在控制界限图中的分布情况,该图中有89%的点超出了故障线,说明此时电路已经严重退化。本文设定溢出率达95%即电路故障。
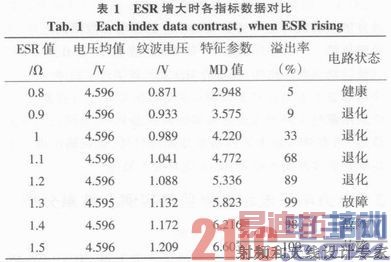
电路健康状态在表1中也已标识出来。由表中数据分析可知,当MD=5.823时溢出率达到99%,可以认定电路已经故障。而MD=3.575~5.336时电路逐渐退化,趋向于发生故障。一般认为输出电压的均值偏离10%或者纹波电压超过1V表示电路故障,表1显示文中所用方法与该标准基本吻合。
表2是电感L从39.2μH减小到21μH的测试结果。C、ESR均取容差为18%,每隔2.6μH进行一次测试,每个测试点做100次高斯分布的蒙特卡洛仿真。
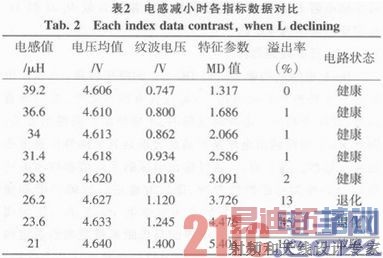
表2数据显示,电感从39.2μH减小到21μH时(幅度接近50%),对电路输出电压和纹波电压影响比较明显。当MD=5.404时,电路发生故障。此时纹波电压已达1.4 V,电感值仅为标称值的44.7%,远超过允许容差。
另设置电容C从200μF减小到90μF,L、ESR均取容差为18%,每隔11μF进行一次测试,每个测试点做100次高斯分布的蒙特卡洛仿真。实验显示,电容从200μF减小到90 μF时(幅度超过50%),对输出电压均值和纹波影响依然很小。即使电容减小到30μF时,对输出影响仍然不明显。从单个元件来说,电路应该已经故障了,但对于整个电路而言,其健康状态并没有实质性的改变。但这种情况在实际电路中不可能出现。电容的明显减小会较快地导致ESR的增大,从而影响输出。
3 结论
通过对Buck电路的健康监测仿真实验研究表明,文中将输出电压的均值和纹波这两个关键参数变换成马氏距离,并通过该特征参数来监测电路健康状态的方法是可行的;并用C、L这2个参数进行了验证。实际运用中不会进行多次蒙特卡洛仿真或者对多个同状态电路进行测试,等价方法是对电路在短时限内进行等时间间隔、连续的状态测试,相当于多次测量时考虑人为误差和电路参数扰动。尚需解决的问题是:实验发现,电路检测为故障的状态与通常的故障表征条件“输出电压的均值偏离10%或者纹波电压超过1 V”有所差异。这可能与健康集的选取、元件容差范围的设定等有关,还需进一步研究确定。


