HFSS15: Conductivity and Permitivitty Limits

The slope parameter K must be > 0. Therefore we must have

This can occur if you enter a DC conductivity higher than the effective conductivity at the measurement frequency. This is impossible in the Djordjevic model, because its conductivity increases monotonically with frequency. Another way for it to happen is for the measurement frequency to be too low (Hz instead of GHz, for example) or for the permittivity value to be unreasonably low.

Therefore from (5) and (7) the following is true.

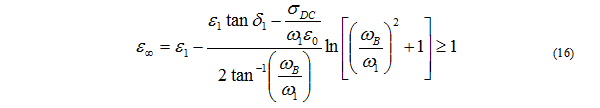
Define the quantity

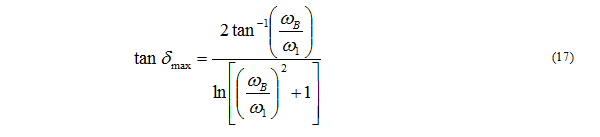
Using this in 16 simplifies the expression as follows.

Then, the condition for passivity can be written as follows:

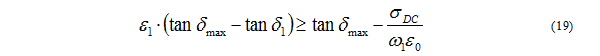
For this to hold, with e > 0, the following two conditions are necessary

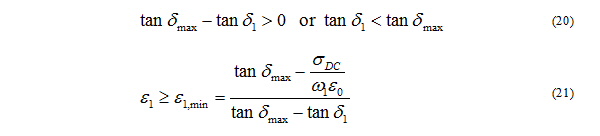
We see from the expression for tan d_max given in (17) that the maximum loss tangent is a function of only the upper corner frequency and the measurement frequency.

Reducing the upper corner frequency will generally increase the value of tan d_max at least as long as the following condition is realized.

But reducing the upper corner frequency is not very attractive, because it has not been observed in experimental data. Therefore it is an upper bound on the loss tangents that the Djordjevic-Sarkar model can handle. Equation (21) indicates that if the permittivity is too low, then the optical permittivity will go below 1. If this condition is violated, two possible fixes are to raise the value of e or to reduce the measurement frequency. But by the same argument as before, reducing the upper corner frequency is not attractive and it is the minimum value of the permittivity. If you reduce the value of the measured loss tangent; this makes the denominator in (21) larger and lowers the value of e_1,min.