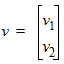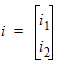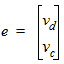- 易迪拓培训,专注于微波、射频、天线设计工程师的培养
HFSS15: Computing Differential Pairs
To obtain various differential pair quantities, we first define differential and common voltages vd ![]() and vc
and vc ![]() in terms of the singled-ended terminal voltage pairs v1
in terms of the singled-ended terminal voltage pairs v1 ![]() and v2,
and v2,![]() (see Setting up Differential Pairs).
(see Setting up Differential Pairs).
The differential and common voltages vd ![]() and vc
and vc ![]() are defined by
are defined by
|
| (1) |
|
|
|
Consistent with power conservation, the corresponding differential and common currents, represented as id ![]() and ic
and ic ![]() respectively, are defined by
respectively, are defined by
|
|
|
Equations (1) and (2) can be concisely represented as
| v = Qe | (3) |
| i = Q-Tu |
|
where
|
|
|
|
• Q ![]() is the real, non-singular matrix defined by
is the real, non-singular matrix defined by
| 
| (4) |
• Q-T ![]() is the inverse transpose of Q
is the inverse transpose of Q ![]() defined by
defined by
| 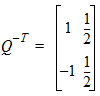
| (5) |
Using eq. (3), we may easily transform between single-ended and differential quantities.
Differential Admittance and Impedance Matrices
The terminal admittance (Y) and impedance (Z) matrices discussed in the previous topics in the Technical Notes relate single-ended voltages and currents as i = Yv and v = Zi, respectively. By first making differential voltage and current definitions, e![]() and u
and u![]() eq. (3) can be used to derive Yd
eq. (3) can be used to derive Yd![]() and Zd
and Zd![]() matrices that relate those qualities.
matrices that relate those qualities.
For example, if i = Yv, then substituting eq. (3) yields
Q-Tu = YQe.
Solving for u ![]() yields
yields
u = QTYQe
and the matrix Yd ![]() relating differential quantities e
relating differential quantities e ![]() and u
and u ![]() is defined by
is defined by
| Yd = QTYQ | (6) |
A similar procedure applies to the terminal Zd.
Differential S-Matrices
It is clear that an S-matrix can be computed for differential signals because it is possible to compute admittance and impedance matrices for differential signals. The differential S-matrix can be envisioned as relating in-going and out-going waves on imaginary transmission lines attached to the differential ports. Characteristic impedances must be specified for these lines unless they are considered to be matched loaded which is automatically the case when the waveport(s) that contain the single-ended terminals used to define the differential pair is not renormalized.
In the single-ended case, the characteristic impedance for a pair of transmission lines may be written in the form of a matrix relating the voltages and currents on the two (uncoupled) lines,
where Z(1)ref and Z(2)ref are the user-specified renormalizing impedances. In the differential case, the matrix equation relating differential and common currents and voltages is written as:
In this case, Z(d)ref and Z(c)ref denote the user-specified differential and common renormalizing impedances, respectively.