HFSS15: Basic DDM Theory

DDM has emerged as a powerful and attractive technique due to its inherent parallelism which enables the use of distributed memory. DDM is based on a divide-and-conquer philosophy where instead of solving a large and complex problem directly, the original problem as defined by the mesh is partitioned into smaller, possibly repetitive, and easier to solve sub meshes or sub-domains. In this approach it is critical to enforce continuity of electromagnetic fields at the interfaces between adjacent sub-domains through some suitable boundary conditions.

To illustrate the basic idea of DDM, we solve (1) by decomposing the original problem into two domains. Subsequently, we have:

(3)

where A_ii, x_i and b_i, i=1,2 are system matrix, solution vector and RHS for domain i, respectively and A₁₂, A₂₁ are the coupling matrices between the two domains. To solve in parallel sub-domain problems, one popular domain decomposition algorithm is of Jacobi type:

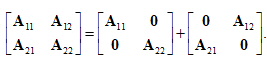
(4)

Using (4) and applying iteration, (3) can be solved as

(5)

Through some simple algebra, equation (5) leads to two coupled systems:

(6)

By setting x₁⁽⁰⁾ = 0 _and x₂⁽⁰⁾ = 0 and, we have initial guess x_i⁽¹⁾ = A_ii^-1b_i which is the local solution of each sub-domain problem. These initial solutions are then refined through coupling matrices A₁₂ and A₂₁ until equilibrium is reached.

The approach (5) is known as a stationary Jacobi solution of (3) which unfortunately converges rather slowly. A more advanced approach is to apply as a preconditioner

leading to:

(7)