HFSS15: Ferrite Permeability Tensor in HFSS

Gyrotropic Permeability

The ferrite capability of HFSS is based on the Polder susceptibility tensor small signal approximation of the Landau-Lifshitz equation of motion of a magnetic dipole in a uniform bias field [1] [2].

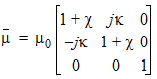
(1)

Where

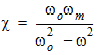
(2)

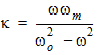
(3)

With

(4)

(5)

(6)

And

(7)

g_e is half of the electron charge to mass ratio and g_l is the Lande g factor. The Lande g factor is typically between 1 and 2, with 1 corresponding to orbital angular momentum and 2 for spin.

If the ferrite has magnetic losses, we replace wo by wo + jwa where a is computed from the ferromagnetic resonance linewidth:

(8)

When HFSS assembles the finite element matrices for ferrite materials it computes the permeability tensor, 1, based on several different inputs:

1. Frequency - w

2. Material properties - all of which are specified in the material manager

a. Saturation Magnetization - Ms

b. Lande g factor - gl

c. Loss factor - computed from DH and fFMR

3. Magnetostatic bias field - Magnetic Bias source, either:

a. Uniform bias - Ho and direction specified in the interface

b. Non-uniform bias - Ho and local tensor direction determined by the magnetostatic field solution from Maxwell3D. When the Magnetic Bias source is nonuniform, the permeability tensor will be different in each ferrite tetrahedron.

References

[1] David Pozar, Microwave Engineering, Addison-Wesley, 1990.

[2] Daniel D. Stancil, Theory of Magnetostatic Waves, Springer-Verlag, 1992.