HFSS15: Linear Constraints

Once the optimization variables are specified, the optimizer handles each of them as an n-dimensional vector x. Any point in the design space corresponds to a particular x-vector and to a design instance. Each design instance may be evaluated via Finite Element Analysis and assigned a cost value; therefore, the cost function is defined over the design space (cost(x): Rⁿ®R), where n is the number of optimization variables.

In practice, a solution of the minimization problem is sought only on a bounded subset of the Rⁿ space. This subset is called the feasible domain and is defined via linear constraints.

You may constrain the feasible domain of a design variable by defining linear constraints for the optimization process. The feasible domain is defined as the domain of all design variables that satisfy all upper and lower bounds and constraints. Linear constraints are defined by the following inequalities:

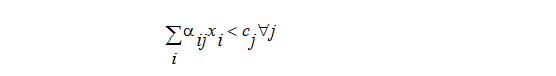
where

• a_ij are coefficients.

• c_j is a comparison value for the j^th linear constraint.

• x_i is the i^th designer parameter.