HFSS15: Multipole Debye Model

The classical Debye model is based on a single pole or time constant. The Multi-Pole Debye Model attempts to generalize the Debye model by adding multiple poles providing greater flexibility in matching arbitrary measurement data.

A lossy dielectric has a complex relative permittivity denoted as follows:

It can be expressed as follows:

where

If the relative permittivity and loss tangent measured at a finite set of frequency points are known, a rational function model can be fit to this data. This approximating rational function can be expressed in pole-residue form as

where

The fitting problem can be expressed as follows: minimize the sum of the least squares differences:

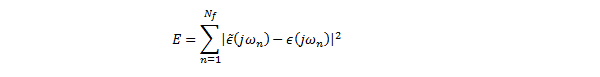
where

HFSS will pre-process the measured data to ensure that it obeys the Hilbert transform (Kramers-Kronig) causality conditions. It then determines a set of stable poles that provide a good model to the frequency variation of the measured data. Finally the residues are determined through least-squares fitting.

The resulting model ensures a causal response for the dielectric when used in time domain simulation. This is because the impulse response of the multi-pole Debye model can be expressed analytically in the time domain as follows:

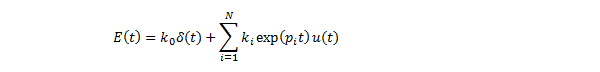
where

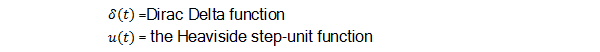
The above impulse response is zero for time t < 0 and so, it is casual.

Recall the approximating multi-pole Debye model function:

After computing this approximating multi-pole Debye model, HFSS splits the model into its real and imaginary parts. The real part corresponds to the approximation for the relative permittivity and the imaginary part divided by the real part gives the approximation for the (negative of the) loss tangent. The resulting (very complicated) expressions are then filled in for the new material model created.