HFSS15: Pattern Search

If the noise is significant in the nominal project, use the Pattern Search optimizer to obtain the results. It performs a grid-based simplex search, which makes use of simplices: triangles in 2D space or tetrahedra in 3D space. A simplex is a Euclidean geometric spatial element having the minimum number of boundary points, such as a line segment in one-dimensional space, a triangle in two-dimensional space, or a tetrahedron in three-dimensional space.

The cost value is calculated at the vertices of the simplex. The optimizer mirrors the simplex across one of its faces based on mathematical guidelines and determines if the new simplex provides better results. If it does not produce a better result, the next face is used for mirroring and the pattern continues. If no improvement occurs, the grid is refined. If improvement occurs, the step is accepted and the new simplex is generated to replace the original one. The figures below illustrate a triangular simplex mirrored several times to demonstrate the pattern search approach in two variables and the simplices superimposed on a 2D cost function to demonstrate the convergence toward a minimum in the cost function.

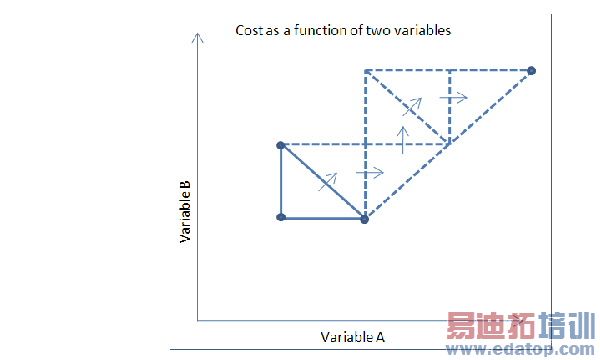
The Pattern Search algorithms are extensible to three variable optimization by using tetrahedral simplices, however, they are not easily represented in graphical form. Generally, Pattern Search algorithms are not used when more than three variables are used in the optimization.

When there is no improvement in the cost function regardless of the direction the simplex is mirrored, then the simplex is subdivided into smaller simplices and the process restarted.

Pattern Search algorithms have several advantages over Quasi-Newton algorithms. First, they are less sensitive to noise because the cost function is evaluated at all node points on the simplex and the numerical noise averages out over the simplex. The second advantage is that the number of initial solutions is generally smaller. However, since the pattern search does not use gradient information to locate the minimum the process converges more slowly toward the true minimum, taking more steps to successively divide the simplices as the minimum is approached.