HFSS15: Rectilinear Elements and Curvilinear Elements

In the Finite Element Method (FEM), the physical domain is subdivided into many small elements. In the global coordinates (x, y, z), the field quantities to be solved are expanded by a set of basis functions. Since the basis functions are associated with each element, it is more convenient to write them in the local coordinates (u, v, w), which are independent of the shape of the element. The local coordinates and the global coordinates are linked by a transformation through a so-called Jocobian.

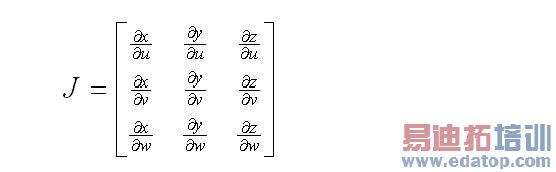
If the transformation is linear, the elements are called rectilinear elements, with straight edges and planar faces; if the transformation is non-linear, such as quadratic or cubic, the elements are called curvilinear elements, with curved edges and/or curved faces. So the curvilinear elements are a more general type of elements than their rectilinear counterparts. While they may not always conform exactly to the curved boundaries, the curvilinear elements conform better with less number of elements than the rectilinear ones. As a result, they generate more accurate and usually faster FEM solutions.