HFSS15: Quasi Newton

If the Sequential Non Linear Programming Optimizer has difficulty, and if the numerical noise is insignificant during the solution process, use the Quasi Newton optimizer to obtain the results. The Quasi Newton optimizer works on the basis of finding a minimum or maximum of a cost function which relates variables in the model or circuit to overall simulation goals. The user marks one or more variables in the project and defines a cost function in the optimization setup. The cost function relates the variable values to field quantities, design parameters like force or torque, power loss, etc. The optimizer can then maximize or minimize the value of the design parameter by varying the problem variables.

Sir Isaac Newton first showed that the maximum or minimum of any function can be determined by setting the derivative of a function with respect to a variable (x) to zero and solving for the variable. This approach leads to the exact solution for quadratic functions. However, for higher order functions or numerical analysis, an iterative approach is commonly taken. The function is approximated locally by a quadratic and the approximation is solved for the value of x. This value is placed back into the original function and used to calculate a gradient which provides a step direction and size for determining the next best value of x in the iteration process.

In the Quasi-Newton optimization procedure, the gradients and Hessian are calculated numerically. Essentially, the change in x and the change in the gradient are used to estimate the Hessian for the next iteration. The ratio of the change in cost to the change in the values of x provides the gradient, whereas, the ratio of the change in the gradients to the change in the values of x provides the Hessian for the next step and is know as the quasi-Newton condition. In order to perform the Quasi-Newton optimization, at least three solutions are required for each parameter being varied. This can have a significant computational cost depending upon the type of analysis being performed.

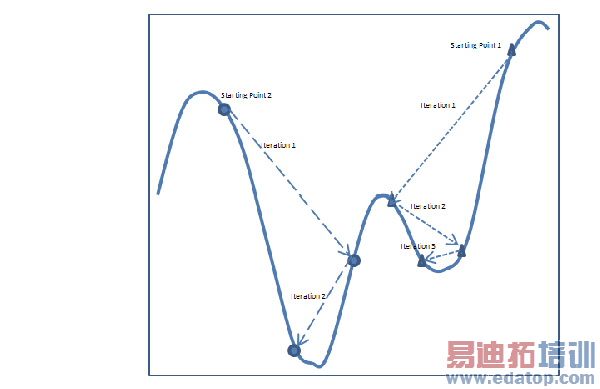
There are numerous methods described in the literature for solving for the Hessian and the details of the method used by Optimetrics are beyond the scope of this document. However, as the Quasi-Newton method is, at its heart, a gradient method, it suffers from two fundamental problems common to optimization. The first is the possible presence of local minima. The figure below illustrates the problem of local minima. In this scenario, you can see that in order to find the minimum of the function over the domain, a number of factors will determine the overall success including the initial starting point, the initial set of gradients calculated, the allowable step size, etc. Once the optimizer has located a minimum, the Quasi-Newton approach will locate the bottom and will not search further for other possible minima. In the example shown, when the optimizer begins at the point labeled "Starting Point 1" the minima it finds is a local minima and not a good global solution to the problem.

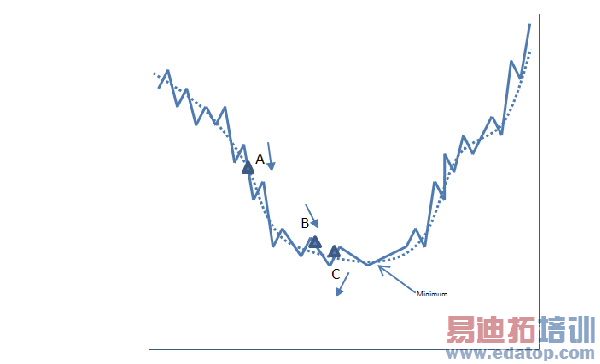
The second basic issue with Quasi-Newton optimization is numerical noise. In gradient optimization, the derivatives are assumed to be smooth, well behaved functions. However, when the gradients are calculated numerically, the calculation involves taking the differences of numbers that get progressively smaller. At some point, the numerical imprecision in the parameter calculations becomes greater than the differences calculated in the gradients and the solution will oscillate and may never reach convergence. To illustrate this, consider the figure shown below. In this scenario, the optimizer is looking for the point labeled "minimum". Three possible solutions are labeled A, B and C, with each arrow indicating the direction of the derivative of the function at that point. If points A and B represent the last two solution points for the parameter, then it is easy to see that the changes in the magnitude and the consistent direction of the derivatives will serve to push the solution closer to the desired minimum. If, however, points A and C are the last two solution points respectively, the magnitude indicates the proper direction of movement, but the derivatives are opposite, possibly causing the solution to move away from the minimum, back in the direction of point A.

In order to use the Quasi-Newton optimizer effectively, the cost function should be based on parameters that exhibit a smooth characteristic (little numerical noise) and a starting point of the optimization should be chosen somewhat close to the expected minimum based on an understanding of the physical problem being optimized. This becomes increasingly difficult, however, when multiple parameters are being varied or when multiple parameters are to be optimized. In addition, the computational burden of multivariate optimization with Quasi-Newton increases geometrically with the number of variables being optimized. As a result, this method should only be attempted when 1 or 2 variables are being optimized as a time.

For more information regarding Quasi-Newton optimization methods, see the following reference:

Schoenberg, Ronald. Optimization with the Quasi-Newton Method. Aptech Systems, Inc. 2001.