HFSS15: Setup Interpolating Sweep Advanced Options

For HFSS and HFSS-IE Interpolating sweeps, the Setup Interpolating Sweep Advanced Options dialog lets you specify the following settings for a sweep:

• The Minimum Solutions value is the minimum number of converged solutions that will be solved for the frequency range. For example, if this value is three, then once the sweep reaches convergence it simulates at two extra frequencies. This resembles the minimum number of converged adaptive passes in a regular simulation. Setting a minimum number of solutions can eliminate non-physical S-parameter spikes and oscillations. For interpolating sweeps the default is 0. To change the value: type a new value in the Minimum Solutions box.

• Specify a Minimum Number of Sub Ranges. This number acts as an initial condition on the sweep to force initial even breakup of the null range into sub ranges. The end points and middle of each subrange will be solved. This controls the points at which the interpolating sweep is broken up and prevents redundant effort caused by neighboring interpolating sweeps solving the same point. For example, the 1GHz to 4GHz and the 4GHz to 9 GHz sweeps do not both solve the 4 GHz data point.

• Whether to use all or selected entries in the matrix of data types for the convergence. To choose, click the Select Entries button to display the Interpolation Basis Convergence dialog.

• The Data Types for Convergence. The defaults selections differ depending on the solution setup.

For Driven modal, Network Analysis 3D Solution Interpolating sweeps:

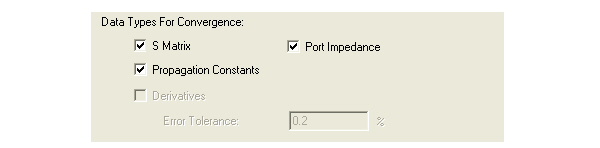
• S-Matrix - checked

• Port Impedance - unchecked.

• Propagation constants - checked.

For Driven terminal, Network Analysis 3D Solution Interpolating sweeps:

• S-Matrix - checked

• Port Impedance - checked.

• Propagation constants - checked.

For Driven modal, Network Analysis ports-only, interpolating

• S-Matrix - unchecked

• Port impedance - checked

• Propagation constants - checked

For Driven terminal, Network Analysis ports-only, interpolating

• S-Matrix - unchecked

• Port impedance - checked

• Propagation constants - checked

If the design contains them, you can select Derivatives. If you select Derivatives, you can also set the Error Tolerance, overriding the tolerance specified in the Edit Sweep dialog..

Enforce Passivity -- This applies to driven modal and Terminal solutions. Select this checkbox to enable passivity enforcement of an interpolating sweep at the requested sampling frequencies with the specified error tolerance. For instance, tolerance of .001 means simulation should attempt to reduce passivity to less than 1.001 at all sampling frequencies. You can view passivity using the reporter.

When using passivity, you may want to increase the Max Solutions value.

During an interpolating sweep, HFSS first adds basis points (solution frequencies) until the convergence goal is reached, and then tests the sampling frequencies using the converged sweep for whether they meet the specified passivity requirement. The sampling frequency having the worst passivity violation is selected for solving. After solving for a passivity violation frequency, the solver adds the newly solved data to the interpolation basis.

If necessary, the solver returns to solving for convergence, limited by the maximum number of solutions for the sweep and resumes passivity checking after reestablishing convergence. Messages in the Solution Profile indicate when the interpolated solver is working towards convergence or working to resolve passivity. If any of the bases violates the passivity, the current sweep terminates with a warning message.

Enforce Causality -- This applies to Terminal solutions. Causality means that an output signal cannot start to change before the input signal changes. A design should follow "Best Practices for Accurate and Causal Broad Band Frequency Sweeps." In addiction, you can select "Enforce Causality" so the sweep fits (rather than interpolates) the s-parameter results to a set of causal basis functions, thereby ensuring the extraction of a causal model..