HFSS15: Step Size

To make the search for the minimum cost value reasonable, the search algorithm is limited in two ways. First, you do not want the optimizer to continue the search if the step size becomes irrelevant or small. This limitation impacts the accuracy of the final optimum. Second, in some cases you do not want the optimizer to take large steps either. In case the cost function is suspected to possess large variations in a relatively small vicinity of the design space, large steps may result in too many trial steps, which do not improve the cost value. In these cases, it is safer to proceed with limited size steps and have more frequent improvements.

For these two limitations, the optimizer uses two independent distance measures. Both are based on user-defined quantities: the minimum and maximum step limits for individual optimization variables. Since the particular step is in a general direction, these measures are combined together in order to derive the limitation for that particular direction.

The step vector between the i^th and (i+1)^th iterate is as follows:

The natural distance measure is,

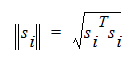
which is the Euclidean norm.

A more general distance measure incorporates some "stretching" of the design space:,

where the matrix D incorporates the linear operation of the stretching of design space. The simplest case is when the D matrix is diagonal, meaning that the design space is stretched along the orthogonal direction of the base vectors.

The optimizer stops the search if,

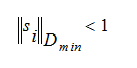
where D_min consists of diagonal elements

equal to the inverse of the Min. Step value assigned to the corresponding optimization variable. Similarly the optimizer truncates steps for which

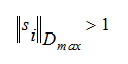
where D_max has diagonal elements equal to the inverse of Max. Step values of the corresponding optimization variables.