【给力】捅一下“三相变单相”问题

一、“三相变单相”、“三相变二相”云云

俄国人说,1888年俄罗斯的多勃罗沃里斯基发明了三相系统,第二年又发明了三相变压器、三相感应电动机; 俄国人又说,1891年,世界上第一条 15KV、200KW、长达175KM 的输电线路在俄罗斯建成并投入运行.从此开始,工业电气化技术的发展步入了快车道.

在三相电力系统的背景下,中小功率的单相电力设备不断出现.这对当时尚捉襟见肘三相电网的负面影响也暴露出来了.于是,不知是不是俄国人又提出了“三相变单相”(以下简称“三变单”)问题.

“三相变二相”(以下简称“三变二”)问题肯定不是俄国人提出的.其解决方案之一“Scott变压器组”在1940年版的变压器手册“The Transformers Book”中就能找到,后来在法国、日本早期的电气化铁道中得到了成功的应用;除Scott方案外,还陆续出现了Lee-Blank、Wood-Bridge等方案;八十年代初同济大学把“三变二”问题概括为“平衡变压器”,对各种方案进行了深入、系统地理论分析,并推出了BLT1、BLT2等新方案.

与“三变二”问题相比,“三变单”问题不那么幸运,因而成了一个很古老的问题.

它的命题应该是:

对称三相电网通过一电气网络(三变单系统),或通过变压器(三变单变压器)对单相负荷供电,使之满足:

a. 电网的三相电流对称;

b. 一次性投入及综合技术性能优于“三相电动机-单相发电机组”.

大功率(达上万KVA)单相工频感应炉的供电方案是“三变单系统”的成功案例.但“三变单变压器”确是近一个世纪来始终悬而未决的问题.应强调的是,这儿的“三变单变压器”的界定是“纯变压器”,即没有任何储能元件,没有任何电力电子功能模块.否则就是“三变单系统”.

虽然随着电力电子技术的飞速发展,这个问题的迫切性已逐渐被淡化.但如果有谁真能提出一个切实可行、满足上述两个条件的“三变单变压器”方案,仍然有相当的市场,仍然能成为轰动国内外变压器制造业的大事!

遗憾的是,没有.这个“没有”是指国内外相关专业杂志上未见刊登过. 但广告里有,或在BBS论坛里能找到哪位高手的相关声明. 对此,下面的话我就不说了.

为 统一认识,这儿有必要插一下“平衡”与“对称”两个术语. “平衡”一词除了数学意义上的“方程式平衡”以外,在电工领域是能量、功率层面的术语.例如平衡变压器输出两端口的功率为使三相“对称”而保持的某种“平衡”;变压器中直接与功率传递相关的磁势平衡等.

三相系统的“对称”是指电压、电流、阻抗层面的术语.

若三相电网对称,符合以下特征,三相线电流才算“对称”:

1) 三相线电流的辐值或有效值相等;

2) 三个线电流的相位彼此相差120度;

3) 与产生它的三相线电压必需同相序.

至于构成对称电网的电压(势),除上述1、2外,还应符合“顺相序”要求. [p]

二、“三变单系统”种种

1、R、L、C 网络.将R、L、C 三元件接成三角形投入三相电网,当L、C 的电抗分别是R 的 1.732 倍时,只要相序合适,R 就是单相负载,且三相对称,功率因数为 1.0 .工频感应炉就这么运行,容量达10 MVA 以上,见图1;

图一

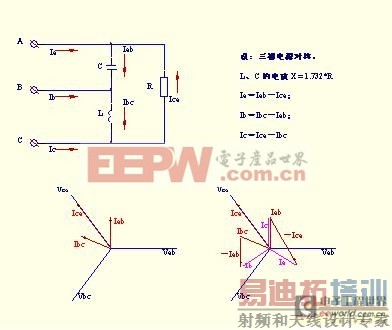
2、 “V”型接法的三相变压器在初级两相间接一电容C,次级绕组串联接一功率因数为0.866的感性单相负载,当负载阻抗是容抗的1.732倍时,初级电流对称,功率因数为0.866(容性),见图2;

图2

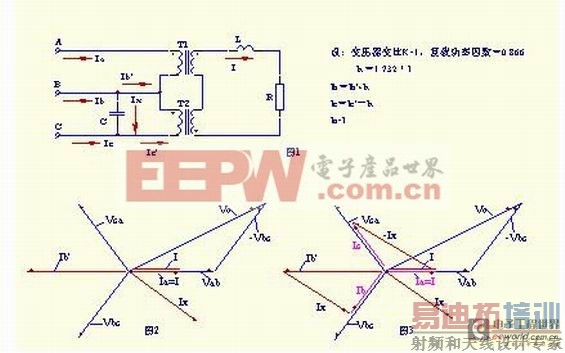
3、在图2的基础上,A、B相间再增加一个电感L,次级负载为纯电阻.L、C 的电抗与折算到初级的电阻相等,则初级电流对称,其大小与折算到初级的电流相等,功率因数为1.0.

上述几方案在应用上的共同特点是:

a、对电网的相序、次级负载性质要求严格;

b、负载要固定.若负载变动,需相应切换储能元件参数.否则将引起初级电流不同程度的不对称.这一缺点方案2 尤为突出.

这就是上述几方案很难在中小功率场合普遍采用的重要原因.

在此说明,只要“三变单系统”里没有非线性元件(合理设计的磁系统在此视为线性),均可逆向运行.例如前苏联早期教科书里能找到上述方案1 的“单相变三相”电路图.

这一特征也适用作为“三变二”问题的平衡变压器.例如,本网站网友jiaoao介绍的“正弦、余弦变三相”的Scott变压器,此时“三变二”已变成“二变三”了. [p]

三、“三变单变压器”——路在何方

（一）、此路不通

套在三相铁心上的各个线圈之间的不同组合,可产生出不同的合成电势相量.这种相量的辐角可以是30度的任意整数倍,相量的大小可以通过改变线圈的圈数任意获得.

这种三相线圈电势的“相量可组合性”特征给“三变单变压器”的探索者们提供了丰富的想象空间——

拼凑一个单相端口,几乎有无穷多个方案……

总能找出很多个合适的方案……

初级三相线电流不就是几个相量段拼出来的吗

调整一下相量段,一直拼到三相电流对称难道不可能吗

问题就出在这儿!

假设某台“三变单变压器”的次级用几个线圈段组合成一个端口(即单相输出端口),这端口电压与产生它的各个相量符合可希苛夫第二定律,或符合某个电压平衡方程式.
或者干脆说:这端口电压是几个电势相量合成的.

但是,这个端口的电流取决于它的负载,与上述相量没有任何关系.再假设这负载电流是 I(I是相量,下同).则任何一个初级线圈电流与次级负载电流 I 的关系由磁势平衡方程式表达.

应注意,不管是哪个初级线圈,磁势平衡方程式所涉的电流相量都与次级负载电流相同,与该线圈所处位置无关.

现把若干个磁势平衡方程式加以整理,得到初级三相线电流的表达式是:

IA＝K1*I ;

IB＝K2*I ;

IC＝K3*I . (1)

按三相线电流对称的条件,(不对称也没关系,按三线制广义节点的可希苛夫第一定律)必然满足:

IA+IB+IC＝0

或 K1+K2+K3＝0 (2)

上式说明: a. 由方程组(1)表达的三相电流相量都在一条直线上,不符合“彼此相差120度”的要求;b. 由式(2)可见,三个实常数相加等于0,它们绝对值不可能彼此相等.

不管线圈如何组合,初级三相线电流不可能对称!

[p]

（二）、各路神仙的“三变单变压器”的不对称度都等同于“相间负载”方案

三相系统用“不对称度”衡量其对称状况。“不对称度”是指三相电流或电压的逆序分量与顺序分量之比。当逆序分量为零或“不对称度”等于零时，三相对称。

仍使用第 15 帖中的（1）、（2）式，令 A 相电流 IA = K1 * I 的顺序、逆序分量分别为 If 和 Ir；为书写方便，再定义常数：

a = exp（-j120）= - 0.5 - j * 1.732 / 2

为顺时针旋转 120 度的旋转因子。按对称分量法，A 相线电流 IA 的顺序、逆序分量分别为：

If = ( K1 + a^2 * K2 + a * K3 ) * I/3

= (- K2 - K3 + a^2 * K2 + a * K3) * I/3

= {( a^2 - 1 ) * K2 + ( a - 1) * K3 } * I/3

= {( -1.5 + j * 1.732 / 2 ) * K2 -

( 1.5 + j * 1.732 / 2 ) * K3 } * I/3

= {( -1.732 * ( K2 + K3 )/2 + j *( K2 - K3 )/2 } * I /1.732 (3)

Ir = ( K1 + a * K2 + a^2 * K3 ) * I/3

= (- K2 - K3 + a * K2 + a^2 * K3) * I/3

= {( a - 1 ) * K2 + ( a^2 - 1) * K3 } * I/3

= {( - 1.732 / 2 + j / 2 ) * K2 +

( - 1.732 / 2 + j / 2 ) * K3 } * I / 1.732

= {( -1.732 * ( K2 + K3 )/2 - j *( K2 - K3 )/2 } * I /1.732 (4)

(3)、(4) 式的 If 、If 均为相量。相量的模（有效值）为：

|If| = |Ir| = I * Sqr{ 3 * (K2 + K3)^2 + ( K2-K3 )^2 } /2/1.732 (5)

使用 (3)、(4)、(5) 式时注意，K1、K2、K3 至少有一个小于 0 。

由(5)式可见，系统的“不对称度” |Ir|/|If| = 1。按“对称分量法”的两个极端情形是：|Ir|/|If| = 0 为完全对称；|Ir|/|If| = 无穷大，即顺序分量为 0 ，相当于电压是顺相序，而电流是逆相序，这是对电网最不利的情形。

前述“相间负载”（即将单相负载跨接于任意两根相线上）可认为是(1)、(2)、(3)、(4) 式的特殊情形。假如将单相负载跨接在 A、B 两根相线上，则 K1 = K ；K2 = -K；K3 = 0 ，其中 K 为跨接在 A、B 相单相变压器的变比；若不用变压器，则K = 1 。将此代入上述各式，可得到相同的结论：不对称度也等于 1 。

（三）、结论

1、现有的“三相变单相”变压器，不管采取何种不使用零线的方案，初级三相电流中最大的一相电流有效值必然等于其余两相电流有效值之代数和；

2、现有的“三相变单相”变压器，不管采取何种方案，其初级三相线电流的“不对称度”均为 1 ；

3、现有的“三相变单相”变压器，不管采取何种方案，其对电网的不利影响均等同于“相间负载”方案；

4、合理地选择单相设备的额定值（额定电压为380伏即可），或仅使用单相变压器直接投入三相电网以构成“相间负载”，可替代现有的“三相变单相”变压器；

5、现有的“三相变单相”变压器，不管采取何种方案，均为浪费资源瞎折腾！