CST2013: Integral Equation Solver Overview

The integral equation solver is of special interest for electrically large models. The discretization of the calculation area is reduced to the object boundaries and thus leads to a linear equation system with less unknowns than volume methods. For calculation efficiency the equation system is solved by the Multi Level Fast Multipole Method (MLFMM) for electrically large models. For the direct solver the system matrix is dense. The integral equation solver is available for plane wave excitation, discrete face ports, waveguide ports, farfield source excitation and RSD current sources. Electric and open boundaries are supported. E-field, H-Field and Farfield monitors and surface current monitors can be set in the Integral Equation Solver.

Overview

Areas of application

• Electrically large simulations

• Fast monostatic  RCS sweep (Definition)

• Scattering parameter matrices (S-Parameter)

• E-field, H-field and surface currents (monitors)

• Farfield and RCS calculations (monitors)

• Windshield antenna simulations (Local multilayer settings)

Frequency sampling

If you are interested in structure's S-parameters, the sampling method has a large influence on the calculation time. Automatically chosen frequency samples in conjunction with the broadband frequency sweep option usually will yield the broadband S-parameters with a minimal number of solver runs. Once the S-parameter sweep has finished, the solver can continue the S-parameter sweep just where it stopped, for instance in order to calculate additional samples, monitors, and further improve the sweep accuracy.

Example: A broadband frequency sweep with automatic sampling

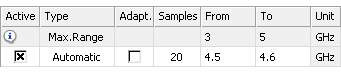
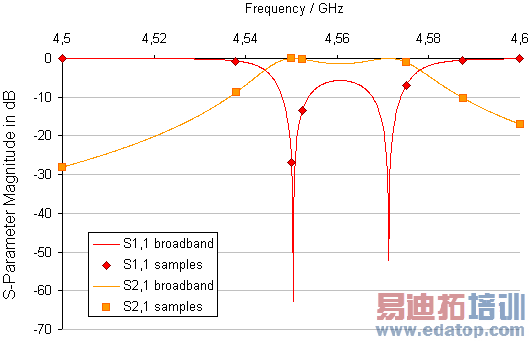
In this example seven frequency samples are calculated in a sub interval of the global frequency range. Please note that less than twenty samples are calculated, since the S-parameter convergence criterion is reached earlier. In this case, the number of frequency samples in the Integral Equation Solver Parameters dialog represents an upper limit.

You will see a quasi continuous curve when the broadband frequency sweep has been activated. The frequency samples are shown when Additional marks is checked in the 1D plot properties dialog, which can be invoked from the context menu when viewing S-parameters. If you deactivate the sweep in the Integral Equation Solver Parameters dialog and press Apply, the samples which actually have been calculated will be shown as well, without the intermediate values.

Example: A broadband frequency sweep with unlimited automatic sampling

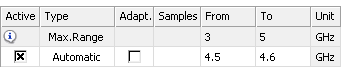
It is not necessary to define a maximum number of sample for the frequency sampling. When the number of samples is not defined (left blank) as shown above, the solver stops calculating additional samples as soon as the S-parameter sweep convergence criterion is satisfied. The results are the same as above, because the S-parameter sweep had converged after calculating seven frequency samples.

Example: A broadband frequency sweep with equidistant sampling

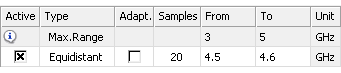
In this example twenty frequency samples are distributed equidistantly in a sub interval of the global frequency range with a frequency spacing of

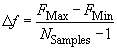
You will see a quasi continuous curve when the broadband frequency sweep has been activated. The frequency samples are shown when Additional marks is checked in the 1D plot properties dialog, which can be invoked from the context menu when viewing S-parameters. If you deactivate the sweep in the Integral Equation Solver Parameters dialog and press Apply, the samples which actually have been calculated will be shown as well, without the intermediate values.

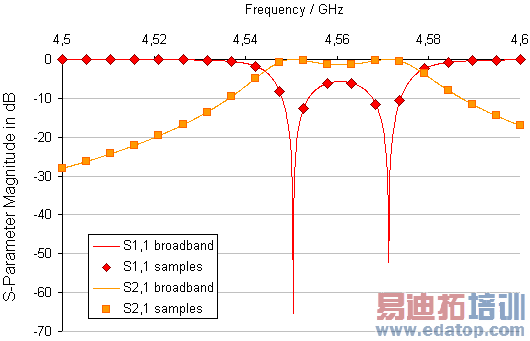
Example: Automatic sampling without broadband sweep

Here twenty samples are calculated, but obviously more samples would be required to get an accurate representation of the S-parameter poles.

Please note that the broadband frequency sweep can be activated again after the simulation run in the Integral Equation Solver Parameters dialog as a post processing step. Check the corresponding box and press Apply.

Supported Materials

A wide range of material is supported by the integral equation solver.

• PEC

• Normal (loss free & lossy)

• Lossy metal

• Ohmic sheet

• all electric frequency dependencies

• Thin panel material: for local multilayer setup

For  material information please see also Material Parameters.

How to start the solver

Before you start the solver you should make all necessary settings. See the Integral Equation Solver Settings for details.

The Integral Equation solver can be started from the Integral Equation Solver Parameters dialog box.

How to create a local multilayer setup

1. Create sheet with layer stackup as thin panel.

2. Thin panel definition requires to attach a WCS. Otherwise it will be ignored.

3. Define metallization as a sheet (PEC-like materials) in reference to defined WCS

4. Use discrete face ports for excitation.

5. Use open (add space) boundary conditions.

6. Thin panel material is not considered automatically.

7. Create a mesh group with local mesh properties to define a local multilayer (Mesh: local multilayer settings).

8. Put all parts which should be in the local multilayer setup (including the thin panel sheet ) into this mesh group.

9. Thin panel will then be considered coupling to metallization.

10. Optional: Define offset for the antenna structure in reference to the defined WCS (Mesh: local multilayer settings).

Solver logfile

After the solver has finished you can view the logfile by choosing Post Processing: Manage Results Logfile . The logfile contains information about solver settings, mesh summary, solver results and solver statistics.

Example for solver logfile:

Units settings:

  Dimensions: m

  Frequency:  MHz

  Time:       s

--------------------------------------------------------------------------------

Boundary conditions:

  YZsymmetry: none

  XZsymmetry: none

  XYsymmetry: none

  Xmin: open

  Xmax: open

  Ymin: open

  Ymax: open

  Zmin: open

  Zmax: open

--------------------------------------------------------------------------------

  Mesh time                : 68 s  (= 0 h, 01 m, 08 s)

--------------------------------------------------------------------------------

================================================================================

Integral Equation Solver calculation cycle started

--------------------------------------------------------------------------------

  Calculation 1 of 1 (Frequency: 150 MHz)

--------------------------------------------------------------------------------

The iterative solver (MLFMM) will be used.

--------------------------------------------------------------------------------

  Matrix setup time               : 1195 s

  Stimulation with                 : Plane wave

  Accuracy                              : 0.00963581

  Degrees of freedom         : 92391

  Iterations                             : 12

  Solver time                          : 1809 s

  Number of surfaces          : 61594

  Solver order                        : 1st

  Far field memory                : 1158.45 MB

  Near field memory             : 83.5853 MB

  Preconditioner memory    : 0.739128 MB

  Number of Level                 : [ 8 ]

--------------------------------------------------------------------------------

Calculation finished.

--------------------------------------------------------------------------------

  Total Solver Time        : 3082 s  (= 0 h, 51 m, 22 s)

================================================================================